PN结中存在的Boltzmann常数
在文章 Measurement of Boltzman’s Constant 作者对, Inman和Miller 在1979年的一个基于晶体三极管测量Boltzmann常数的时间进行的复现和讲解。作为电子学教育的一个很好的文章。

01 PN结的电压与电流
在PN结两边由于电子热扩散以及随后引起的电子-空穴的复合,形成的耗散区域,产生了一个 V 0 V_0 V0的接触电位,并形成了PN结内部的电场 E d E_d Ed。 E d E_d Ed是 V 0 V_0 V0除以PN物理等效宽度。
在n型半导体内部的电子的热动能呈现Boltzmann分布:
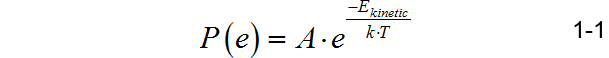
这其中动能大于 e ⋅ V 0 e \cdot V_0 e⋅V0的电子数量应该是:
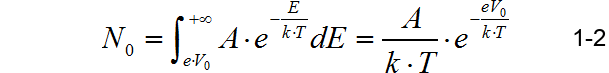
这表明可以越过PN结内部电场的电子数量是V0的指数函数。假设其中有一定比例的电子正好越过PN结,这样就形成了扩散电流,它的形式为 原文 中的公式(1):
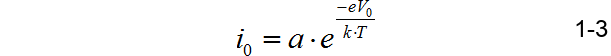
由PN结内部电场 E d E_d Ed会使得一部分在p型半导体的电子(包括扩散来的电子以及p型半导体内部热运动产生的电子)流向n型半导体,形成逆向(与扩散电流相反)电流。在平衡下,电场 E d E_d Ed引起逆向电流等于(1-3)对应的扩散电流, i 0 i_0 i0。
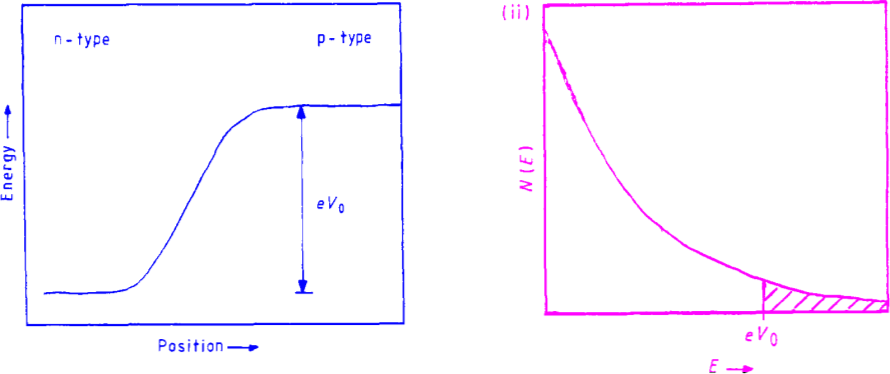
▲ PN结两边的势能以及电子的Boltsmann分布
当PN结施加正向电压(从p型半导体指向n型半导体) V V V后,PN结两边的电位差就变成了 V 0 − V V_0 - V V0−V,形成的扩散电流就变成了:
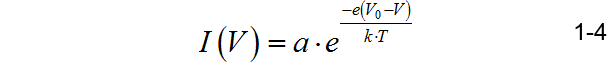
在施加了正向电压之后,PN结内部的电场应该也发生了变化。所产生的逆向电流并没有变化,这是因为逆向电流是对那些漂移到p型半导体耗散层的电子的总和(因为它们都会被内电场发送到n型半导体耗散层),这些电子没有发生变化,所以逆向电流依然是(1-3)公式对应的值。
根据公式(1-4),(1-3),扩散电流减去逆向电流就是观察到的PN结的导通电流:

这就得到了PN结电流与电压之间的关系。通常,由于 e e V 0 k T e^{{{eV_0 } \over {kT}}} ekTeV0远远大于1,所以可以将(1-5)公式括号中的1省略掉。
在上述公式中,还有其他的因素会影响指数的系数,最后的公式可以写成:
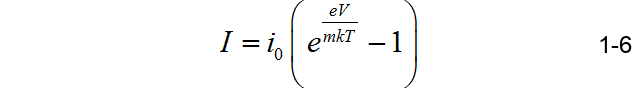
其中m可以取值从1到2.5。
02三极管内的PN结电流
在三极管中,如果集电极与基极之间的电位 U b − c U_{b - c} Ub−c始终保持为0时,那么发射极与基极之间的电流与PN结之间的关系就由(1-5)来决定了。
因此,如果把三极管的集电极电流 I c I_c Ic作为发射极-基极之间电压 U b − e U_{b - e} Ub−e的关系的话,那么就有:
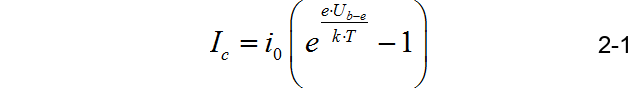
这个方程也被称为:Ebers-Moll方程。
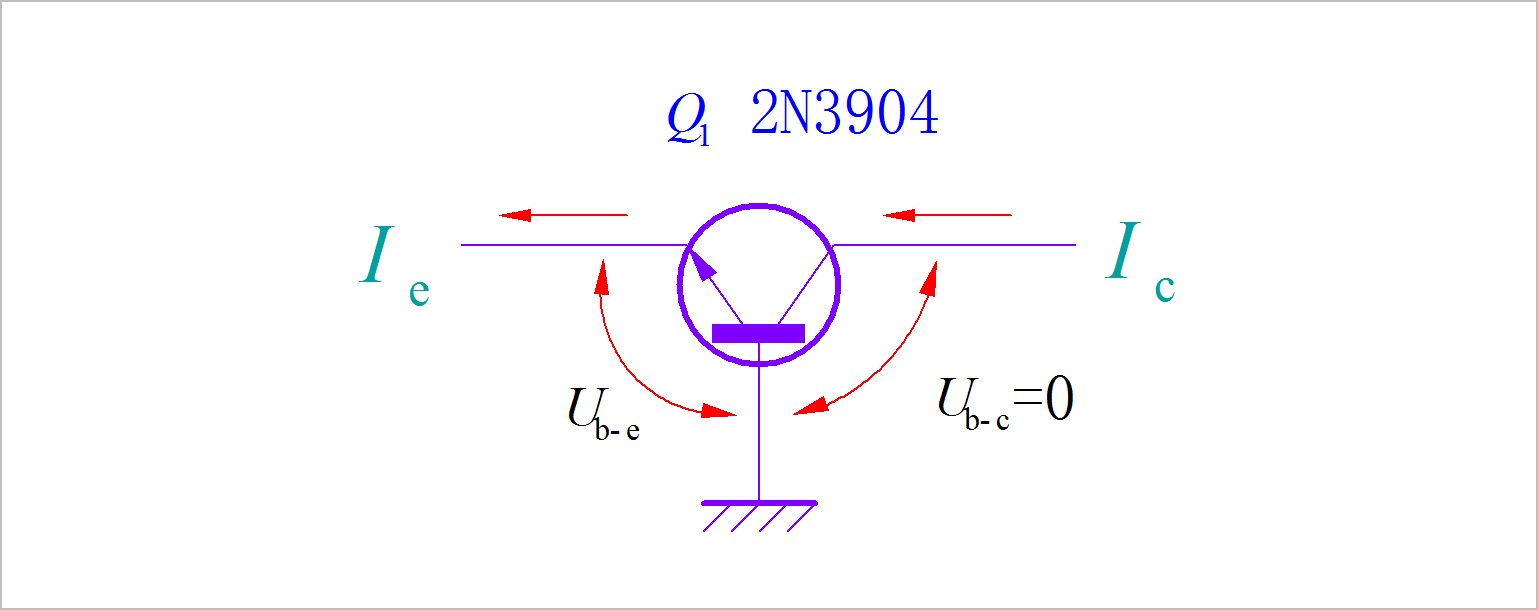
▲ 三极管的发射极与集电极电流
公式(2-1)是所有基于三极管PN结来测量Boltzmann常数的基础。
下图是摘自1973年Inman,Miller论文中的电路图,其中使用了PNP型 晶体管TIP29(30) 的b-PN结来测量,图中的R选取1MΩ至10kΩ,取决于测量电流的范围。
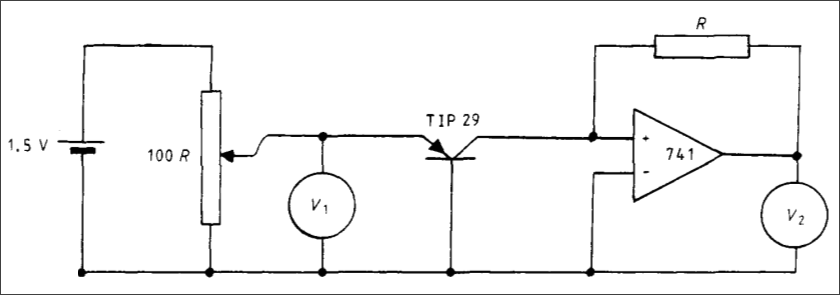
▲ 测量三极管TIP29PN结电流和电压关系的电路
使用中,使用了较为便宜的运放 741 对集电极电流进行电压转换。为了消除 741 较大的偏置电压,可以将TIP29 与运放断开,测量出对应的偏移量,最后从测量数据中扣除其影响即可。
图中采用了TIP29是一个大型功率三极管,可以通过散热片来保证晶体管内部温度与环境温度相一致。
也可以将上述三极管浸泡在绝缘油里来控制三极管的温度。
下图是原论文中给出的在不同的反馈电阻R下,也就是在不同的电流范围内测量的电流与电压之间的关系。其中电流使用了对数,这样就得到了电流与电压之间的线性关系。
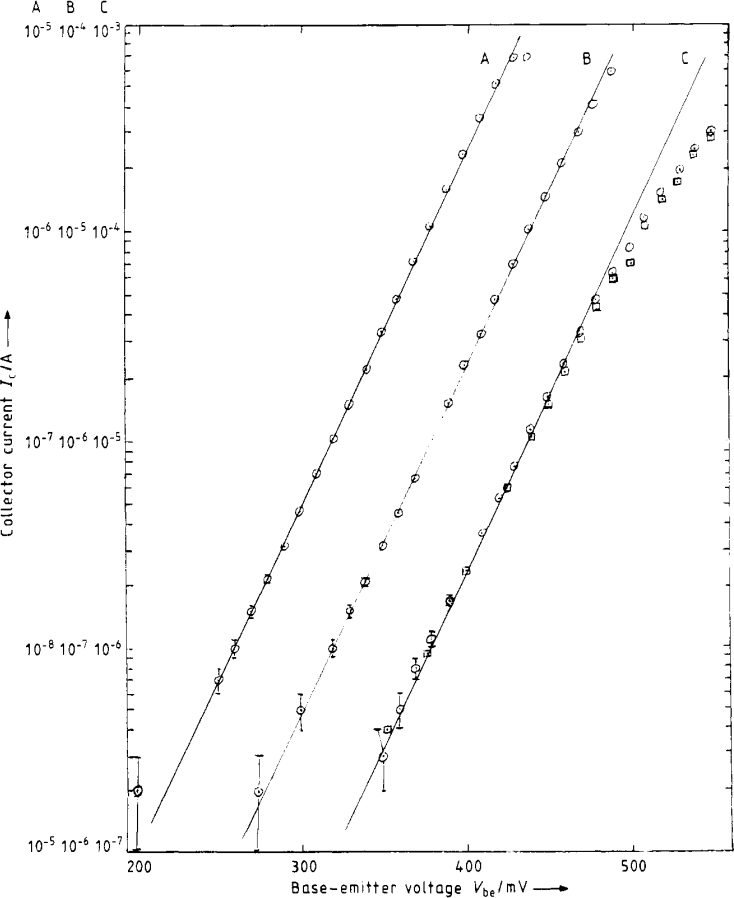
▲ 分别在三种不同的反馈电阻向测量的结果
图中对于大电流下(测量线C)出现的偏差,原来来自于PN结内的电阻存在对于电压的影响。
※ 结论
上面的是揣进来自于1986年的Physics Education(Great Britain)的文章,作者对于1973年的Inman, Miller给出的方案进行了复现。得益于精密的数字万用表以及使用计算机进行数据除拆除,所获的Boltzmann常数的精度达到了3%的范围。
这个实验是验证Boltzmann分布规律的简单明了的一个电子实验。
实际上,选择不同的测量电流范围,所得到的Boltzmann的常熟也会发生变化。在博文 利用二极管的P-N结的I-V特性测量Boltzmann常数 中给出了一组不同的配置方案下所得到的结果。
文章来源: zhuoqing.blog.csdn.net,作者:卓晴,版权归原作者所有,如需转载,请联系作者。
原文链接:zhuoqing.blog.csdn.net/article/details/107136205
- 点赞
- 收藏
- 关注作者


评论(0)