单层神经网络-Logistics回归中误差曲线
➤01 Logistic回归
Logistic回归通常用于处理二类分类问题。本质上它是单层神经网络模型。
1.问题
给出对象的特征向量: x = { x 1 , x 2 , ⋯ , x n } x = \left\{ {x_1 ,x_2 , \cdots ,x_n } \right\} x={x1,x2,⋯,xn}
得到一个预测结果: y ^ = P { y = 1 ∣ x } \hat y = P\left\{ {y = 1|x} \right\} y^=P{y=1∣x}

▲ Logistic回归模型
2. Logistic回归
首先进行线性回归:
z = W T ⋅ x ˉ + b z = W^T \cdot \bar x + b z=WT⋅xˉ+b
然后在使用一个Sigmoid函数得到预测结果: y ^ = s i g m o i d ( z ) = 1 1 + e − z \hat y = sigmoid\left( z \right) = {1 \over {1 + e^{ - z} }} y^=sigmoid(z)=1+e−z1
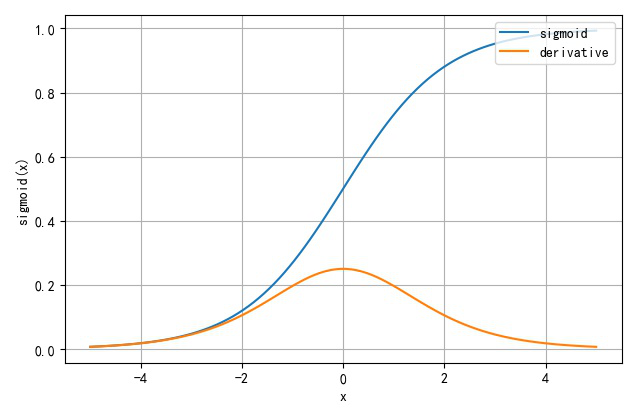
▲ Sigmoid函数以及它对应的导数
def sigmoid(x):
return 1/(1+exp(-x))
def dsigmoid(x):
x = sigmoid(x)
return x*(1-x)
x = linspace(-5, 5, 100)
z = sigmoid(x)
dz = dsigmoid(x)
plt.plot(x, z, label='sigmoid')
plt.plot(x, dz, label='derivative')
plt.xlabel("x")
plt.ylabel("sigmoid(x)")
plt.grid(True)
plt.legend(loc='upper right')
plt.tight_layout()
plt.show()
➤02 简单举例
1.逻辑与
使用Logistic回归来实现逻辑与逻辑:
(1) 与逻辑
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
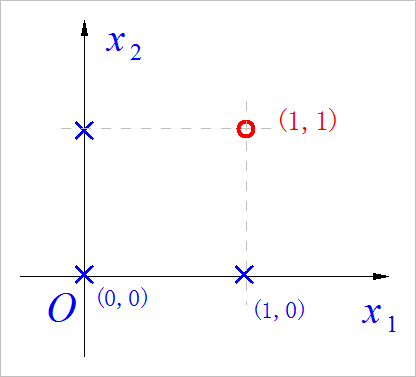
▲ AND逻辑示意图
(2) Logistic回归
z = w 1 ⋅ x 1 + w 2 ⋅ x 2 + b z = w_1 \cdot x_1 + w_2 \cdot x_2 + b z=w1⋅x1+w2⋅x2+b y ^ = 1 1 + e − z \hat y = {1 \over {1 + e^{ - z} }} y^=1+e−z1
定义损失函数:
L ( y ^ , y ) = 1 2 ( y ^ − y ) 2 L\left( {\hat y,y} \right) = {1 \over 2}\left( {\hat y - y} \right)^2 L(y^,y)=21(y^−y)2
那么总的损失函数为:
L ( y ^ , y ) = ∑ i = 1 4 1 2 ( y ^ i − y i ) 2 L\left( {\hat y,y} \right) = \sum\limits_{i = 1}^4 {{1 \over 2}\left( {\hat y_i - y_i } \right)^2 } L(y^,y)=i=1∑421(y^i−yi)2
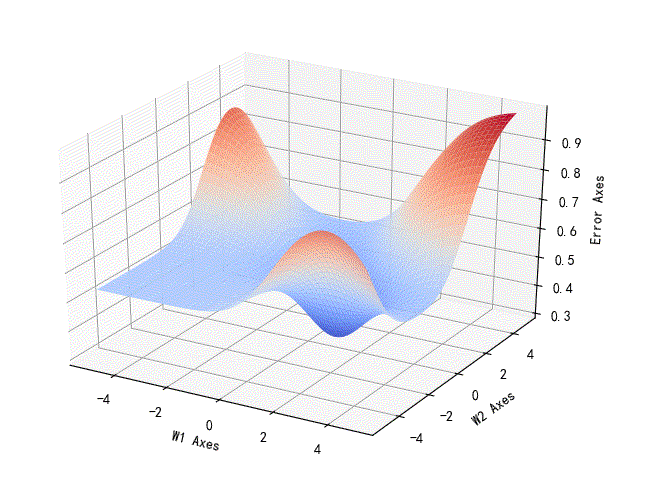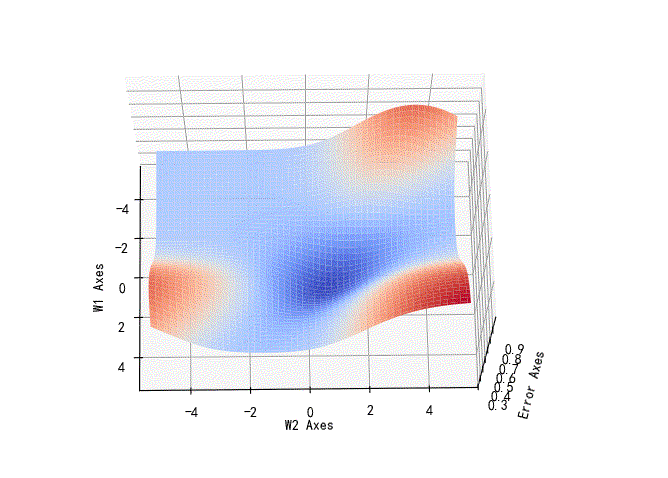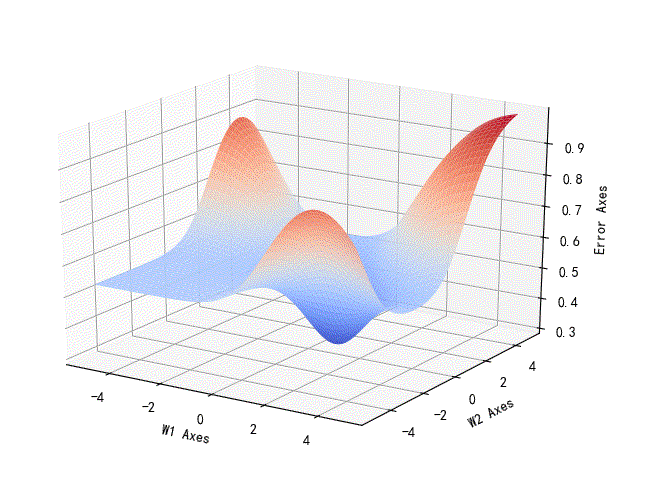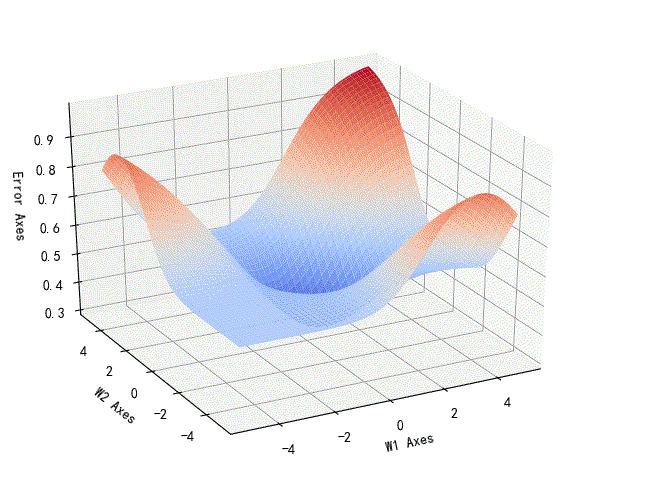
▲ W1,W2相对的误差曲线
可以看到这个误差相对于W1,W2是一个非凸的误差曲线。
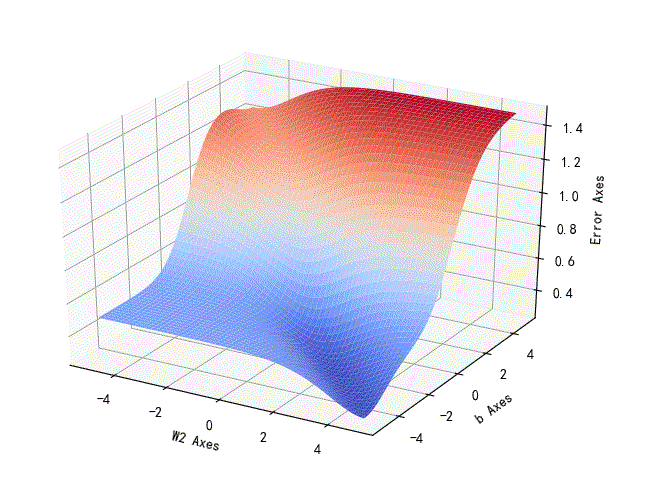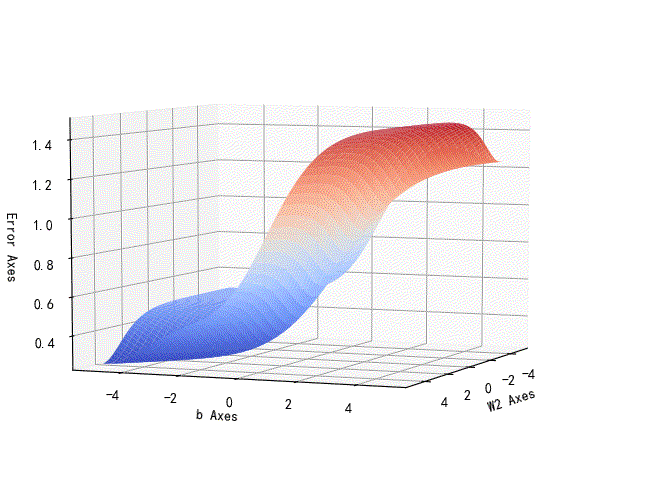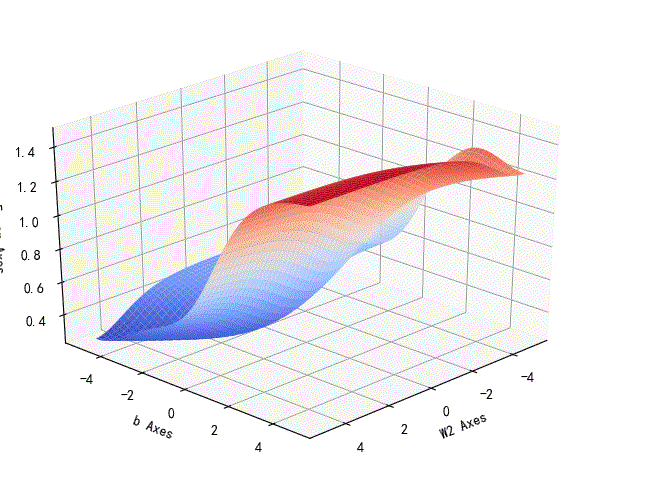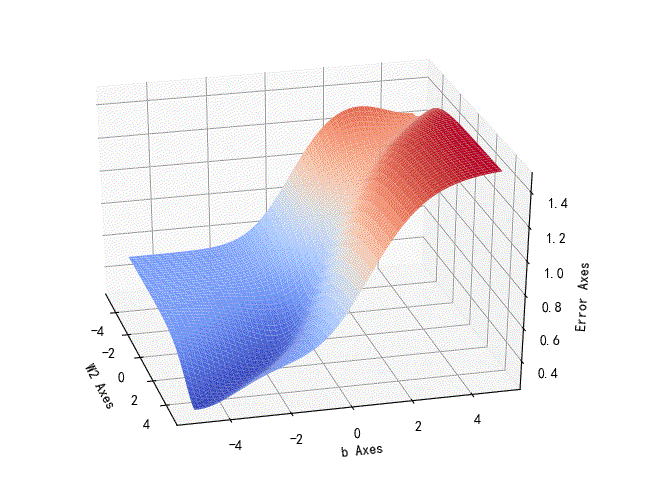
▲ W2,b参数误差平面
#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# LOGTEST.PY -- by Dr. ZhuoQing 2020-11-17
#
# Note:
#============================================================
from headm import *
from mpl_toolkits.mplot3d import axes3d
from matplotlib import cm
b=-1
#------------------------------------------------------------
def sigmoid(x):
return 1/(1+exp(-x))
def error(w1,w2):
z00 = b
z01 = w1+b
z10 = w2+b
z11 = w1+w2+b
y00 = sigmoid(z00)
y01 = sigmoid(z01)
y10 = sigmoid(z10)
y11 = sigmoid(z11)
_y00 = 0
_y01 = 0
_y10 = 0
_y11 = 1
res = (y00-_y00)**2 +\
(y10-_y10)**2 +\
(y01-_y01)**2 +\
(y11-_y11)**2
return res/2.0
#------------------------------------------------------------
w1 = arange(-5, 5, 0.1)
w2 = arange(-5, 5, 0.1)
W1,W2 = meshgrid(w1, w2)
E = error(W1, W2)
ax = plt.axes(projection='3d')
ax.plot_surface(W1, W2, E, cmap='coolwarm')
ax.set_xlabel('W1 Axes')
ax.set_ylabel('W2 Axes')
ax.set_zlabel('Error Axes')
plt.show()
#------------------------------------------------------------
# END OF FILE : LOGTEST.PY
#============================================================
如果取对数似然损失函数:
L ( y ^ , y ) = − [ y ⋅ log ( y ^ ) + ( 1 − y ) ⋅ log ( 1 − y ^ ) ] L\left( {\hat y,y} \right) = - \left[ {y \cdot \log \left( {\hat y} \right) + \left( {1 - y} \right) \cdot \log \left( {1 - \hat y} \right)} \right] L(y^,y)=−[y⋅log(y^)+(1−y)⋅log(1−y^)]
根据前面定义,总损失函数为:
L ( y ^ , y ) = log ( 1 − y ^ 11 ) L\left( {\hat y,y} \right) = \log \left( {1 - \hat y_{11} } \right) L(y^,y)=log(1−y^11)
L ( y ^ , y ) = log ( 1 − 1 1 + e − w 1 − w 2 − b ) L\left( {\hat y,y} \right) = \log \left( {1 - {1 \over {1 + e^{ - w_1 - w_2 - b} }}} \right) L(y^,y)=log(1−1+e−w1−w2−b1)
对数似然损失函数相对于w1,w2的变化曲面:
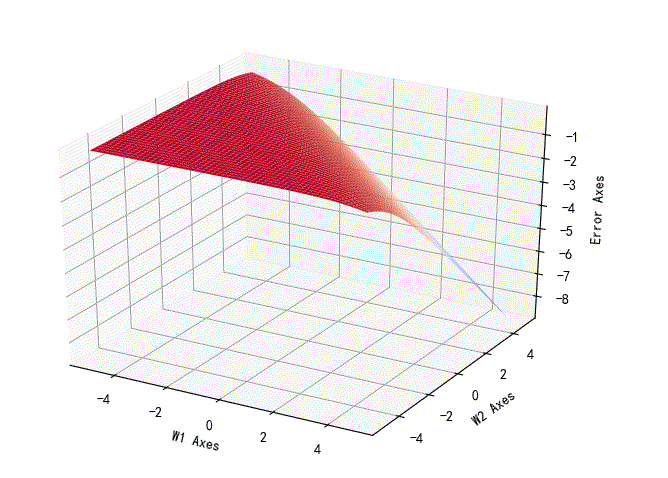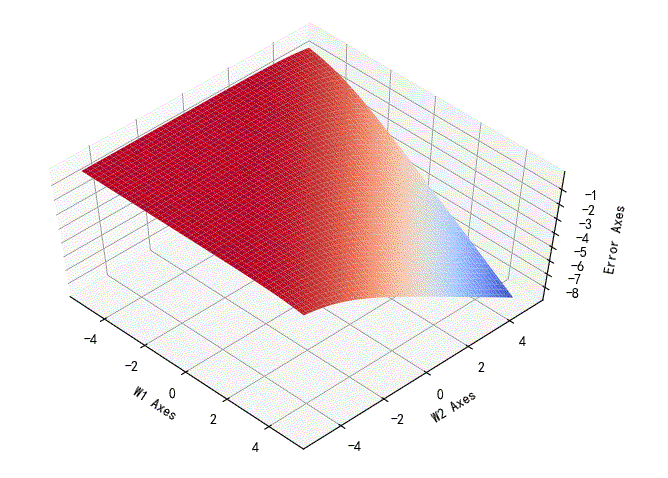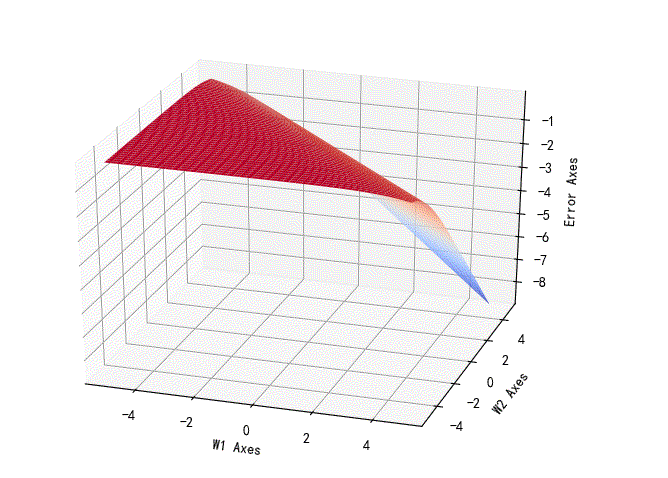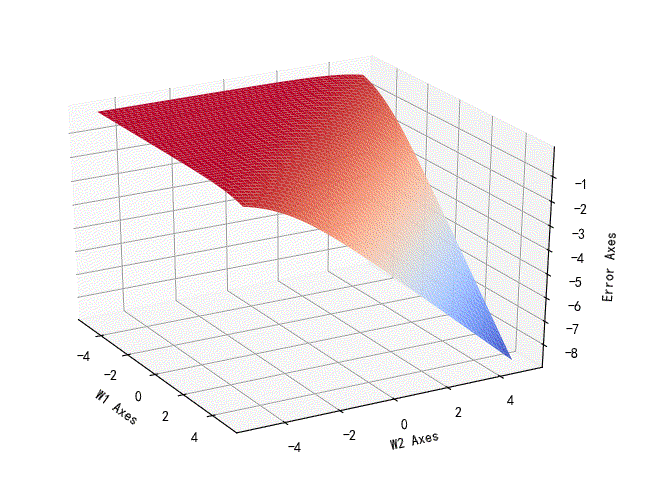
▲ 对数似然损失函数
w2,b参数对应的损失误差曲面:
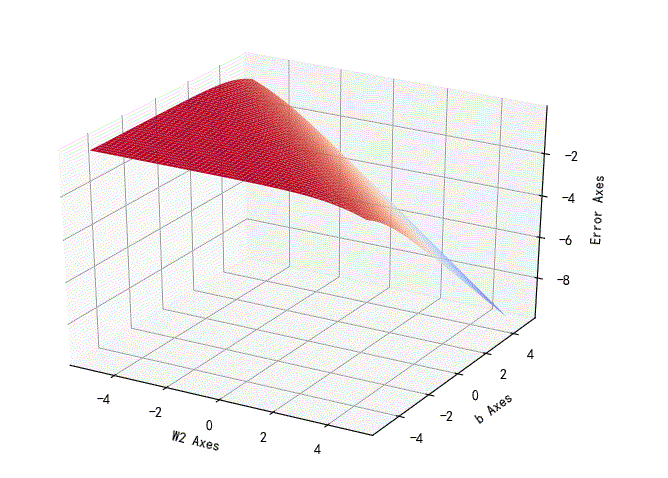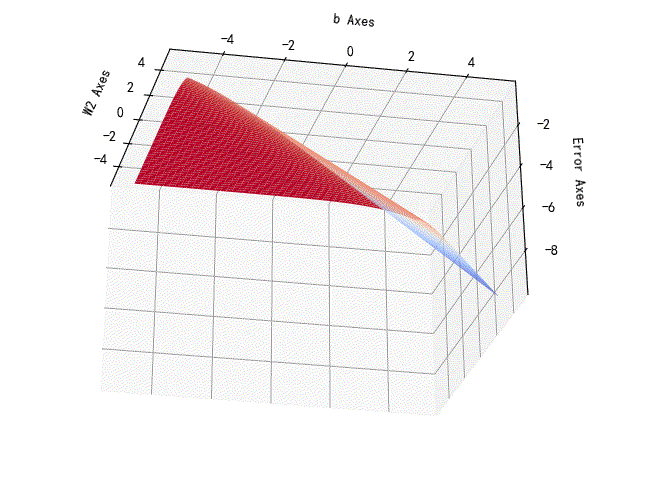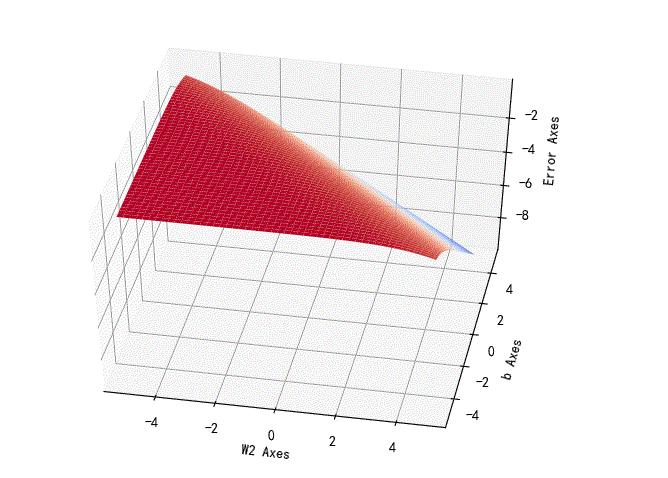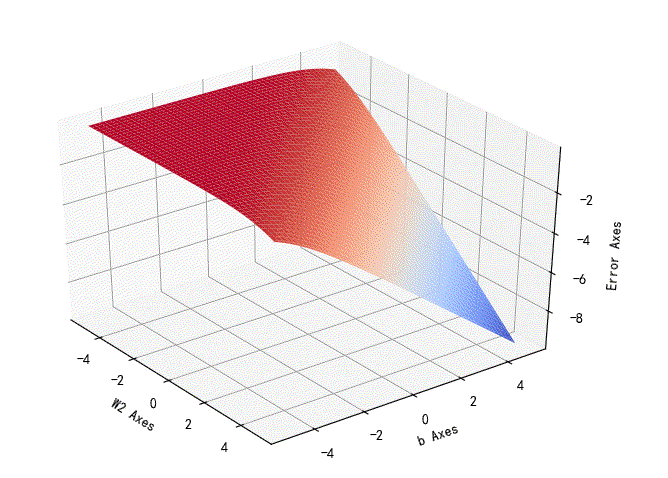
➤03 线性可分与不可分
使用Logistic回归来进行分类,它只能个解决线性可分的问题。下面对于逻辑与和逻辑异或所组成的Logistic回归所对应的参数的误差平面的特点。
1.逻辑与w1,w2的误差曲面
从下面的曲线可以看到,误差曲线的最低值小于0.5,也就是说,如果恢复到逻辑值,这样的误差是可以回归到0的。因此,使用Logistic回归的时候是可以正确的区分逻辑与分类的。
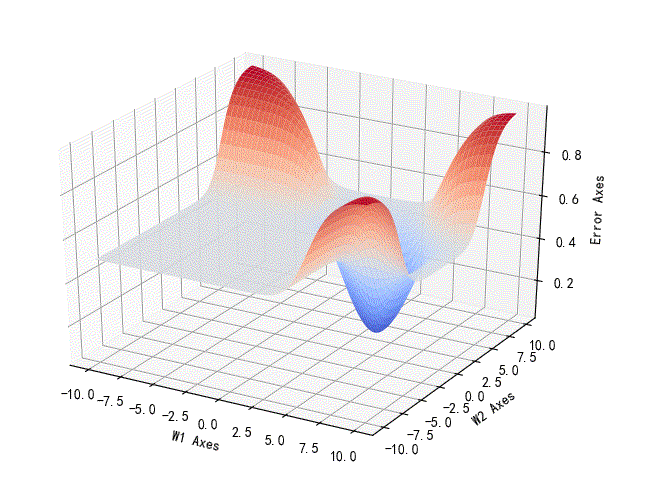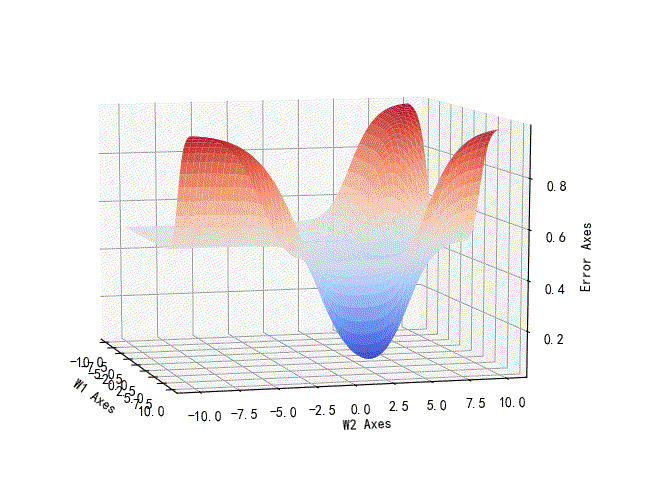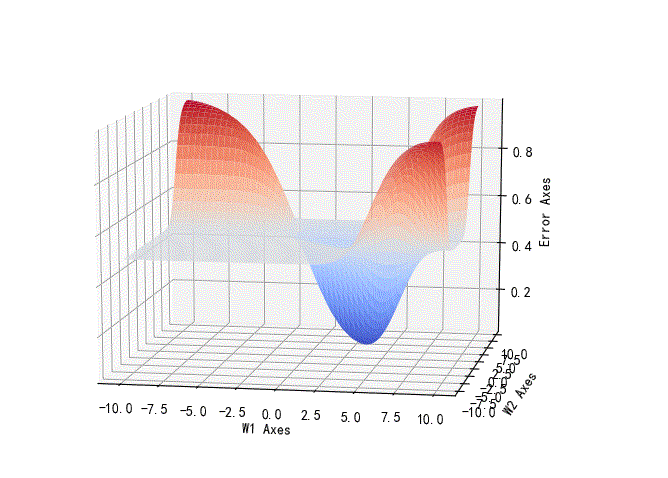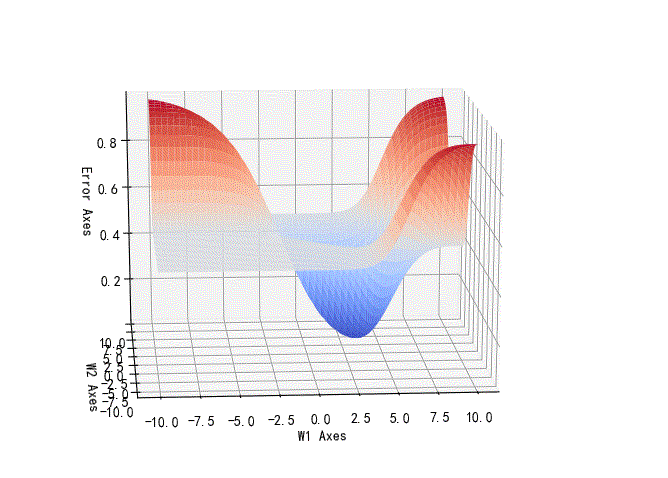
▲ 逻辑与的参数误差曲线
2.逻辑异或的参数误差曲线
下面的曲线则显示的是逻辑异或的关系。可以看到它的最低值仍然是大于0.5的。这也说明该网络无法区分逻辑异或(这是一个非线性可分的问题)的种类的。
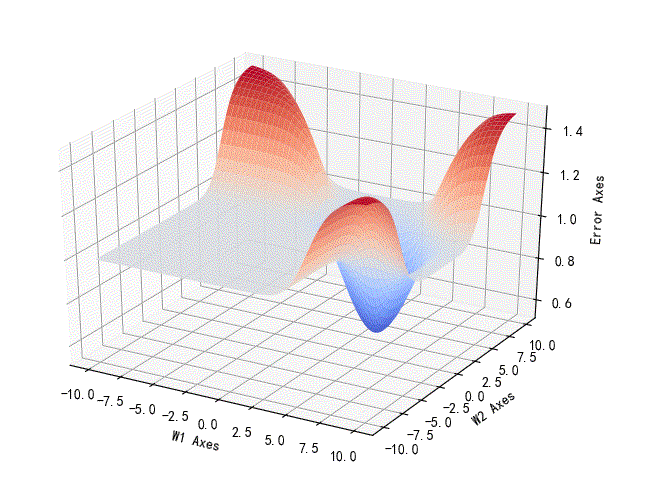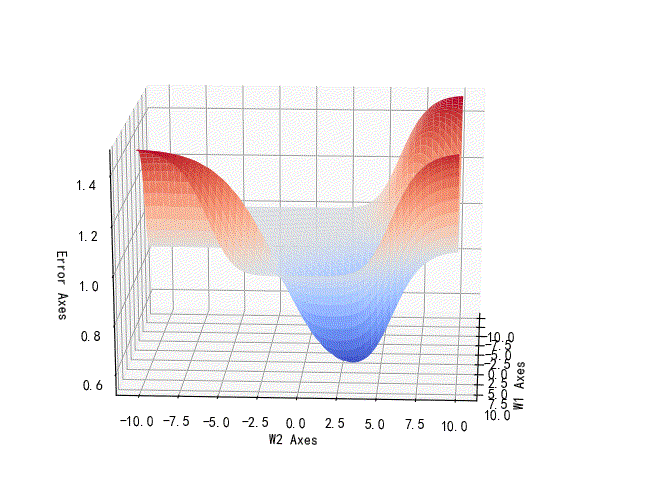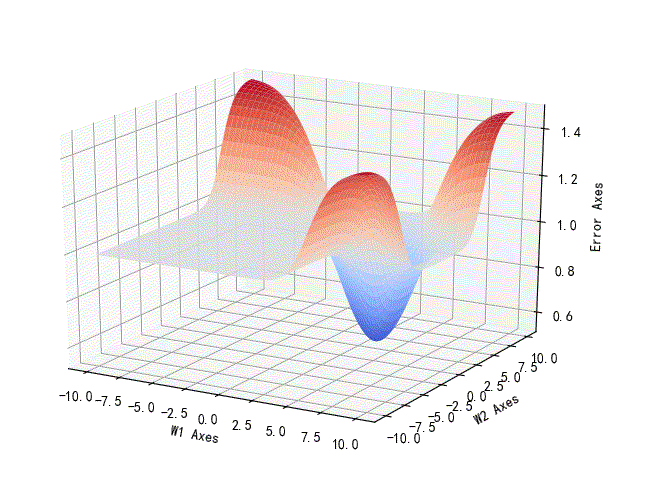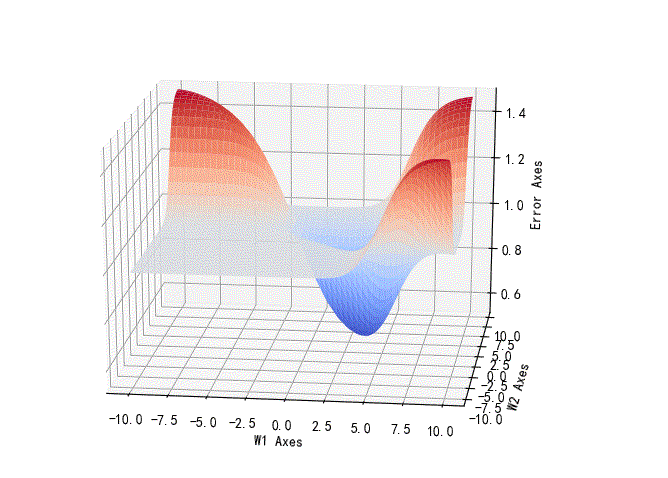
▲ 异或逻辑的参数误差曲线
➤※ 结论
为什么在Logistic回归中,对于损失函数不再使用均方差 L ( y ^ , y ) = 1 2 ( y ^ − y ) 2 L\left( {\hat y,y} \right) = {1 \over 2}\left( {\hat y - y} \right)^2 L(y^,y)=21(y^−y)2,而使用对数似然函数 L ( y ^ , y ) = − [ y ⋅ log y ^ + ( 1 − y ) ⋅ log ( 1 − y ^ ) ] L\left( {\hat y,y} \right) = - \left[ {y \cdot \log \hat y + \left( {1 - y} \right) \cdot \log \left( {1 - \hat y} \right)} \right] L(y^,y)=−[y⋅logy^+(1−y)⋅log(1−y^)]
通过逻辑与函数对比了这两种误差相对于参数的变化曲线,可以看到:
使用均方差进行Logistic回归的时候,误差曲线往往是非凸的,而使用对数似然损失函数,参数优化问题往往变成了凸优化。
通过Logistic参数误差曲线也可以分别出该网络是否可以解决相关的分类问题。对于线性可分的问题,使用Logitisc回归是可以区分的。但对于非线性可分的问题,使用Logistic无法解决。
■ 相关文献链接:
#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# LOGTEST.PY -- by Dr. ZhuoQing 2020-11-17
#
# Note:
#============================================================
from headm import *
from mpl_toolkits.mplot3d import axes3d
from matplotlib import cm
#------------------------------------------------------------
def sigmoid(x):
return 1/(1+exp(-x))
def error(w1,w2,b):
z00 = b
z01 = w1+b
z10 = w2+b
z11 = w1+w2+b
y00 = sigmoid(z00)
y01 = sigmoid(z01)
y10 = sigmoid(z10)
y11 = sigmoid(z11)
_y00 = 1
_y01 = 0
_y10 = 0
_y11 = 1
# return log(1-y11)
res = (y00-_y00)**2 +\
(y10-_y10)**2 +\
(y01-_y01)**2 +\
(y11-_y11)**2
return res/2.0
#------------------------------------------------------------
w1 = arange(-10, 10, 0.1)
w2 = arange(-10, 10, 0.1)
W1,W2 = meshgrid(w1, w2)
E = error(W1, W2, -5)
ax = plt.axes(projection='3d')
ax.plot_surface(W1, W2, E, cmap='coolwarm')
ax.set_xlabel('W1 Axes')
ax.set_ylabel('W2 Axes')
ax.set_zlabel('Error Axes')
plt.show()
#------------------------------------------------------------
# END OF FILE : LOGTEST.PY
#============================================================
文章来源: zhuoqing.blog.csdn.net,作者:卓晴,版权归原作者所有,如需转载,请联系作者。
原文链接:zhuoqing.blog.csdn.net/article/details/109733951
- 点赞
- 收藏
- 关注作者


评论(0)