向量、矩阵的范数--Lp定义
➤01 向量范数(Norm)
1.定义
对于向量 x ˉ \bar x xˉ的范数 L p L_p Lp定义如下:
∥ x ˉ ∥ p = ( ∑ i ∣ x i ∣ p ) 1 p \left\| {\bar x} \right\|_p = \left( {\sum\limits_i^{} {\left| {x_i } \right|^p } } \right)^{{1 \over p}} ∥xˉ∥p=(i∑∣xi∣p)p1
通常情况下,对于给定的 x ˉ \bar x xˉ, L p L_p Lp的数值与 p p p有关系。当如果 x x x是标量,那么 ∥ x ∥ p \left\| x \right\|_p ∥x∥p与 p p p五个。
对于 p p p的几个特殊的取值, ∥ x ˉ ∥ p \left\| {\bar x} \right\|_p ∥xˉ∥p取值如下:
(1) p = 1:
∥ x ˉ ∥ 1 = ∑ i ∣ x i ∣ \left\| {\bar x} \right\|_1 = \sum\limits_i^{} {\left| {x_i } \right|} ∥xˉ∥1=i∑∣xi∣
(2) p = 2 : ∥ x ˉ ∥ 2 = ∑ i x i 2 \left\| {\bar x} \right\|_2 = \sqrt {\sum\limits_i^{} {x_i^2 } } ∥xˉ∥2=i∑xi2
(3) p = ∞
∥ x ˉ ∥ ∞ = max i ∣ x i ∣ \left\| {\bar x} \right\|_\infty = \mathop {\max }\limits_i \left| {x_i } \right| ∥xˉ∥∞=imax∣xi∣
2.举例
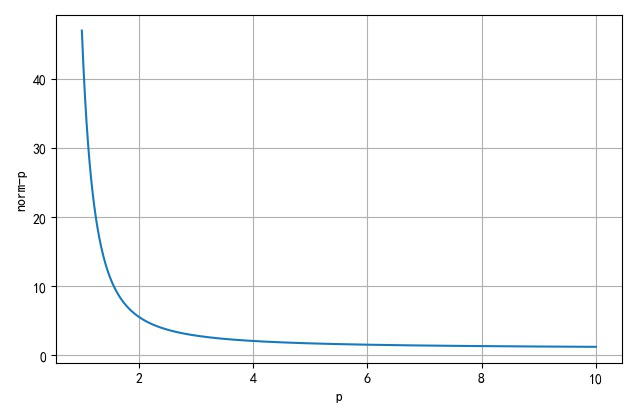
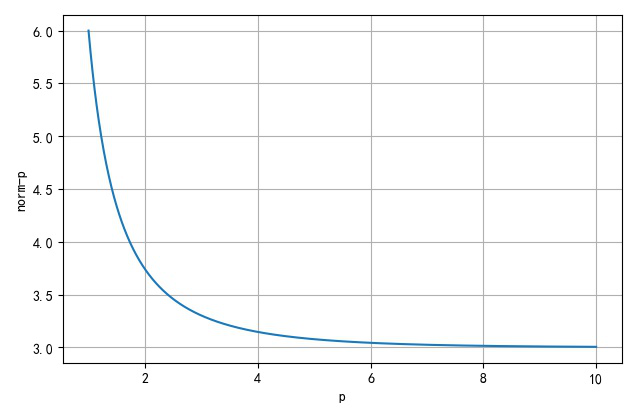
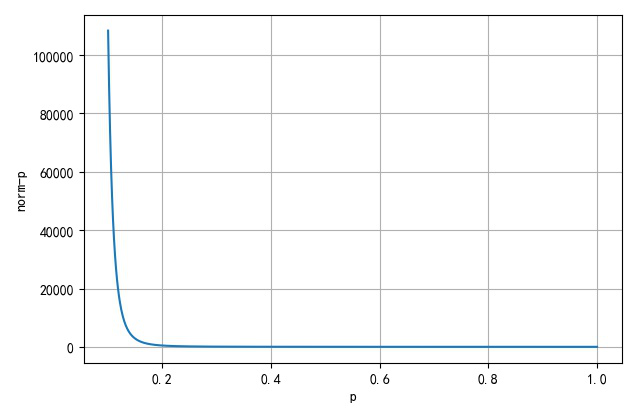
令 x ˉ = ( 1 , 2 , 3 ) \bar x = \left( {1,2,3} \right) xˉ=(1,2,3),那么下面绘制 ∥ x ˉ ∥ p \left\| {\bar x} \right\|_p ∥xˉ∥p的取值随着p值的变化曲线:
def normp(x,p):
sumup = sum(list(map(lambda r:pow(r,p), x)))
return pow(sumup, 1/p)
- 1
- 2
- 3
计算三种不同的范数:1, 2, 无穷大。
∥ ( 1 , 2 , 3 ) ∥ 1 = 6 , ∥ ( 1 , 2 , 3 ) ∥ 2 = 3.74165 , ∥ ( 1 , 2 , 3 ) ∥ ∞ = 3 \left\| {\left( {1,2,3} \right)} \right\|_1 = 6,\,\,\,\left\| {\left( {1,2,3} \right)} \right\|_2 = 3.74165,\,\left\| {\left( {1,2,3} \right)} \right\|_\infty = 3 ∥(1,2,3)∥1=6,∥(1,2,3)∥2=3.74165,∥(1,2,3)∥∞=3
-
P的取值1 ~ 10:

▲ 不同p下的Norm(x)p的取值 -
p取值: 0.1 ~ 1:

▲ 不同p下的Norm(x)p的取值
3.随机向量
向量 x ˉ \bar x xˉ去维度为100的随机向量。
[0.24391919 0.49622443 0.47875403 0.09911819 0.55347071 0.62541928
0.09802366 0.06835364 0.91876807 0.15899439 0.36288558 0.33701167
0.54999295 0.0884227 0.44314682 0.06830299 0.77773741 0.77438765
0.20816862 0.92733654 0.95196255 0.67490874 0.02014755 0.30706064
0.5241224 0.55222905 0.10500043 0.29495123 0.36738073 0.54551681
0.30690897 0.60352366 0.65770245 0.41998395 0.37576451 0.15260377
0.73901666 0.1658365 0.71668991 0.24563881 0.05607063 0.31411558
0.07276439 0.01767733 0.58261071 0.47360638 0.79779543 0.60401737
0.13094089 0.96497742 0.31550006 0.80261193 0.75992481 0.32960755
0.09673154 0.69607499 0.82705553 0.85927744 0.365921 0.80895228
0.41148695 0.54490593 0.79370549 0.31457977 0.03542475 0.74360923
0.59775384 0.64370262 0.42894051 0.18293789 0.71454713 0.53763004
0.80207508 0.70567435 0.6587668 0.24039822 0.85006424 0.48574726
0.15490323 0.37997356 0.9104184 0.09877531 0.14219021 0.76059397
0.10229202 0.26434798 0.57522697 0.62408809 0.67169252 0.13293343
0.95223045 0.39905133 0.69676899 0.19756753 0.46648849 0.5882844
0.01855678 0.56824342 0.53406079 0.17367655]
计算结果:
|x|1=45.98593560996123
|x|2=5.337567743508142
|x|100=0.9692209010245963

▲ 不同p下x的模
➤02 矩阵的范数
可以使用 L p L_p Lp范数来衡量矩阵 A A A的Frobenius的范数:
∥ A ∥ F = ( ∑ i , j ∣ A i j ∣ 2 ) 1 2 \left\| A \right\|_F = \left( {\sum\limits_{i,j}^{} {\left| {A_{ij} } \right|^2 } } \right)^{{1 \over 2}} ∥A∥F=(i,j∑∣Aij∣2)21
x = random.rand(10,10)
[[5.77241118e-01 4.47299620e-01 9.34225154e-01 1.37258546e-01 3.37849651e-01 4.47679381e-01 8.59109821e-01 2.11646551e-01 2.45356994e-01 8.57916498e-01]
[1.00530952e-01 4.36903342e-01 9.18364036e-01 1.82207010e-01 5.76999771e-01 6.19150194e-01 7.39193214e-02 1.97617365e-01 6.82669986e-01 8.51328166e-01]
[4.83637083e-01 7.95432871e-01 6.93688731e-02 4.85649135e-01 7.41136158e-01 8.47261623e-01 7.17975880e-01 5.81934362e-01 5.96811915e-01 3.57037450e-01]
[1.31650902e-01 8.39763071e-01 2.63461873e-01 2.88515824e-01 9.52160127e-01 2.92993997e-01 5.60513678e-01 4.03694431e-01 8.59689217e-01 9.34598738e-01]
[2.80716836e-01 1.94946229e-01 1.06277652e-01 7.94070539e-01 1.34892914e-01 8.81801705e-01 3.07759782e-01 1.25711105e-01 1.00572082e-01 7.23696797e-01]
[3.86884885e-01 8.73714370e-01 8.38268405e-01 2.67326998e-01 3.64319371e-01 9.42436607e-01 2.97936522e-01 7.82813446e-01 5.88709624e-01 4.61394418e-01]
[1.26953155e-01 5.02286444e-01 1.21772318e-01 5.33498663e-01 2.78981602e-01 2.26861308e-01 9.35817193e-01 7.54270179e-01 7.74004901e-01 3.14405051e-01]
[8.51522674e-01 9.10788029e-02 3.05078260e-02 1.82766662e-01 1.74375026e-01 6.71277145e-01 9.68754183e-01 9.38809087e-01 2.34603156e-01 2.77403139e-01]
[8.16678016e-05 4.10596294e-01 3.83992576e-01 7.24796836e-01 4.01949558e-02 4.84989102e-01 3.94557881e-01 9.38897942e-01 7.21536817e-01 2.83264496e-01]
[5.02283358e-01 1.67694058e-01 1.27423082e-01 5.51798902e-02 4.71489390e-01 5.56747951e-02 7.79663082e-01 1.02021506e-01 8.57441393e-01 1.07593011e-01]]
仍然使用前面定义的normp()对它进行求取范数。
#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# TEST1.PY -- by Dr. ZhuoQing 2020-11-16
#
# Note:
#============================================================
from headm import *
def normp(x,p):
sumup = sum(list(map(lambda r:pow(r,p), x)))
return pow(sumup, 1/p)
x = random.rand(10,10)
printf(x)
x2 = normp(x, 2)
x1 = normp(x, 1)
x00 = normp(x, 100)
printff(x1, x2, x00)
pdim = linspace(1, 10, 1000)
xdim = []
for p in pdim:
xdim.append(normp(x, p))
plt.plot(pdim, xdim)
plt.xlabel("p")
plt.ylabel("norm-p")
plt.grid(True)
plt.tight_layout()
plt.show()
#------------------------------------------------------------
# END OF FILE : TEST1.PY
#============================================================
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
▲ 不同p对应着不同的范数-p
➤※ 结论
使用 L p L_p Lp范数可以对于向量、矩阵定义出对应的范数。使用这些范数可以来度量向量、矩阵的模。
文章来源: zhuoqing.blog.csdn.net,作者:卓晴,版权归原作者所有,如需转载,请联系作者。
原文链接:zhuoqing.blog.csdn.net/article/details/109729874
- 点赞
- 收藏
- 关注作者


评论(0)