超简单的主成分分析（PCA）协方差矩阵算法及其相关性分析热力图

相信了解过PCA的小伙伴都知道怎么求协方差矩阵的公式

下面直接给出求相关性矩阵计算代码及热力图

import seaborn as sns;sns.set(color_codes= True)

# 相关性分析
def covriance(data):    # 传入的数据集-data
    X = d.corr()
    print(X)
    sns.heatmap(X,square=True, annot=True)
    plt.title("Correlation matrix")
    plt.show()
if __name__ == "__main__":
	covriance(dataset)

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
 

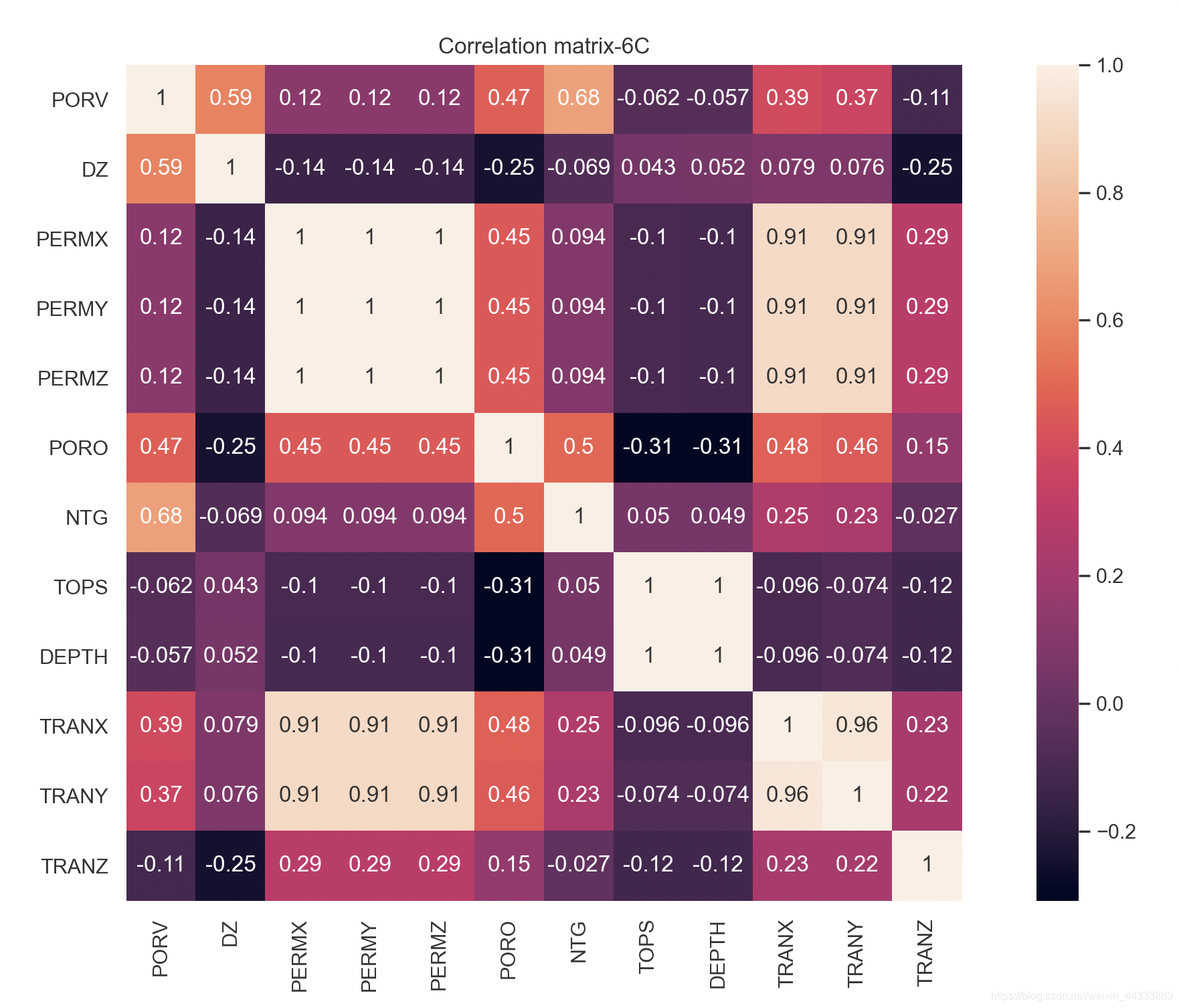
相关性热力图效果如下

"

我们之所以痛苦，是因为有比较。

"

❤️

文章来源: blog.csdn.net，作者：府学路18号车神，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/weixin_44333889/article/details/118341157