⚡可行梯度方向法⚡(Feasible Gradient Direction Method ,FGDM)
⚡最近很烦⚡
有一阵子没更新了,感觉整个暑假被忽悠了,六月份找Boss指明了一个Direction,然后整个暑假都在忙于补充Proposal相关的Knowledge,但是,被忽悠局局长Boss给忽悠了(谁人能明白其中的难受),干工科的master怎么可能不依靠数据,本来就知道拿不到数据,还跟着让指哪儿打哪儿,最终项目还是拿不到,唉~,Project always Project(Boss),一心就只有Project,这还让等到Sep去Proposal,调研的都白费了,谁爱去Proposal谁去。终究或许还是自己太菜了。
Sometimes one pays most for the things one gets for nothing.
最近看到算法比较多,其中发现一个FGD(Feasible Gradient Direction)方法,可行梯度方向法,很是疑惑,到处寻找答案,找不到。和Zoutendijk可行方向法相比好像又有所区别,下面根据Paper的SEDA(sparse exponential discrimination analysis)稀疏指数判别分析算法求解其目标函数进行解释一下(菜鸡的自我修养)。
背景
首先,先介绍一下背景,之前出过一篇LDA的解释Blog,LDA主要用于降维和简单分类,在多分类问题上比较有用。
在过去的几十年里,针对LDA方法提出过很多中改进的方法,如惩罚判别分析(PDA)、两阶段主成分判别分析(PCA+LDA)、零空间LDA(NLDA)、指数判别分析(EDA)、灵活判别分析(FDA)、混合判别分析(HDA)、稀疏判别分析(SDA)等等…一系列改进方法。
最近研究到一篇是关于对指数判别分析(EDA)的改进方法—稀疏指数判别分析(sparse exponential discrimination analysis,SEDA)。
简单来说一下作者的改进路线。
EDA
指数判别分析(EDA)则是将LDA的类内和类间协方差矩阵 S b 、 S w \mathbf{S_b、S_w} Sb、Sw分别进行了指数化操作(这里所说的指数化操作可能在专业上描述的不太准确,理解万岁),如下
原本LDA的目标函数长这样:
J = w T S b w w T S w w J=\frac{\boldsymbol{w}^{\mathrm{T}} \mathbf{S}_{b} \boldsymbol{w}}{\boldsymbol{w}^{\mathrm{T}} \mathbf{S}_{w} \boldsymbol{w}} J=wTSwwwTSbw
而改进的EDA的目标函数长这样:
J = w T Σ b w w T Σ w w J=\frac{\boldsymbol{w}^{\mathrm{T}} \mathbf{\Sigma}_{b} \boldsymbol{w}}{\boldsymbol{w}^{\mathrm{T}} \mathbf{\Sigma}_{w} \boldsymbol{w}} J=wTΣwwwTΣbw
注意,其中
Σ b = e x p ( S b ) Σ w = e x p ( S w ) \mathbf{\Sigma}_{b}=exp(\mathbf{S}_{b}) \\ \\ \mathbf{\Sigma}_{w}=exp(\mathbf{S}_{w}) Σb=exp(Sb)Σw=exp(Sw)
此为改进的地方,可使用类间距离与类内距离的比率来评估判别分析方法的性能。
SEDA
现在我们加上EDA的约束条件,
max w k w k T Σ b w k s.t. w k T Σ w w k = 1 w k T Σ w w i = 0 ( ∀ i < k ) \max _{w_{k}} \ \ \ \ w_{k}^{T} \Sigma_{b} w_{k}\\ \\
max w k w k T Σ b w k s.t. w k T Σ w w k ≤ 1 w k T Σ w w i = 0 ( ∀ i < k ) \max _{w_{k}} \ \ \ \ w_{k}^{T} \Sigma_{b} w_{k}\\ \\
max w k w k T Σ b w k − γ ∥ w k ∥ 1 s.t. w k T Σ w w k ≤ 1 w k T Σ w w i = 0 ( ∀ i < k ) \max _{w_{k}} w_{k}^{T} \Sigma_{b} w_{k}-\gamma\left\|w_{k}\right\|_{1} \\
γ \gamma γ
一般来说,随着lasso惩罚因子 γ \gamma γ的增加,SEDA算法的模型可解释性和判别性能有所提高,但当 γ \gamma γ超过一定程度时,情况正好相反。
(中间过程过于复杂已忽略)
最终变形为下面这样的目标函数(为凸函数,原本为非凸函数,估计是为了增加一个创新点吧或许,本来可以直接拉格朗日干起来,搞非凸函数求其最优解,现在改进使用最小化-最大化(MM)算法将其重新表达为一个迭代凸优化问题变为凸函数,学到了):
max v v T Σ b k w k i − γ ∥ v ∥ 1 s.t. v T Σ w v ≤ 1 (*)
可行梯度方向法
这里主要针对稀疏判别优化的可行梯度方向法,将(*)式的约束优化问题转变为无约束优化问题,(公式太多了,就不打公式了哈)
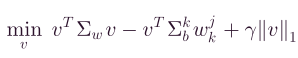
上式的Hessian矩阵显然是对称正定的。因此,上式的无约束优化问题是严格凸的,这意味着其极值点对应于最优解。首先将上式的优化问题简化为一个标准的二次规划问题,然后利用一种可行的梯度方向法来有效地求解该问题。
将上式进行进一步优化,
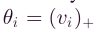 和
和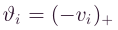 ,其中 ( x ) + (x)_+ (x)+表示正部分运算符, ( x ) + = m a x { 0 , x } (x)_+=max\{0,x\} (x)+=max{0,x},因此,向量v可以重写为,
,其中 ( x ) + (x)_+ (x)+表示正部分运算符, ( x ) + = m a x { 0 , x } (x)_+=max\{0,x\} (x)+=max{0,x},因此,向量v可以重写为,
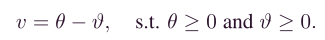
同理,原无约束优化函数变为,
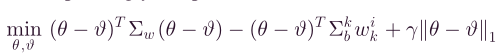
再将二次项重新表述为,
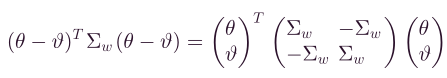
同样的,
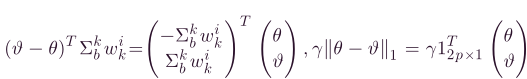
因此,无约束优化的问题可以简化为一个标准的二次规划(二次规划凸优化有个好处,就是,局部最优解即为全局最优解),
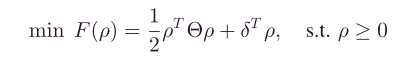
其中,
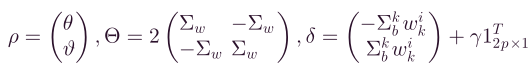
下面是关于可行梯度方向法的核心观点:
可行梯度方向法的思想如下图所示。在图中,我们假设点 O O O是上式无约束优化问题最简化公式后的最优解。黑色虚线是点 O O O的轮廓线,红色实线是优化问题的约束条件。对于如图所示的满足目标函数约束条件的给定初始迭代点 ρ 0 ρ_0 ρ0,其可行方向 f ( ρ 0 ) f(ρ_0) f(ρ0)显然是 ρ 0 ρ_0 ρ0的梯度方向, f ( ρ 0 ) = ▽ F ( ρ 0 ) f(ρ_0)=\bigtriangledown F(ρ_{0}) f(ρ0)=▽F(ρ0)。让 ρ 1 = ρ 0 − κ × τ × f ( ρ 0 ) ρ_1=ρ_0-\kappa\times\tau\times f(ρ_0) ρ1=ρ0−κ×τ×f(ρ0),其中 τ 0 τ_0 τ0是 ρ 0 ρ_0 ρ0的最佳步长, κ κ κ是调谐参数 ( 0 ≤ κ ≤ 1 ) (0≤ κ ≤ 1) (0≤κ≤1). 在 ρ 1 ρ_1 ρ1在约束条件内的情况下,选择尽可能大的 κ κ κ,这样我们就可以计算点 ρ 1 ρ_1 ρ1。正如点 ρ 1 ρ_1 ρ1, y y y方向的 ∇ F ( ρ 1 ) ∇F(ρ_1) ∇F(ρ1)将导致点不满足约束条件,因此选择 x x x方向上的 ∇ F ( ρ 1 ) ∇F(ρ_1) ∇F(ρ1)作为可行方向 F ( ρ 1 ) F(ρ_1) F(ρ1),这就是所谓的可行梯度方向法。对点 ρ 1 ρ_1 ρ1执行与 对 ρ 0 对ρ_0 对ρ0相同的操作,并递归执行此过程,直到收敛。
简单说来,就是在图中,找一个起始点作为开始的出发点 ρ 0 ρ_0 ρ0,然后按照目标函数的梯度方向进行寻找,其中有两个超参数(暂且这么称呼吧) k 、 τ k、\tau k、τ,用于对下一次寻找做参数调节作用。在到达如图 ρ 1 ρ_1 ρ1的地方后,红色实线是我们的约束条件,要使得更快的找到最优解 O O O,可以按照图中 y y y或者 x x x的方向进行寻找,图中的按照 y y y方向的话, ∇ F ( ρ 1 ) ∇F(ρ_1) ∇F(ρ1)将导致点不满足约束条件,故就换方向,按照 x x x的方向作为可行方向 F ( ρ 1 ) F(ρ_1) F(ρ1),然后再不断的重复 ρ i + 1 = ρ i − κ × τ × f ( ρ i ) ρ_{i+1}=ρ_i-\kappa\times\tau\times f(ρ_i) ρi+1=ρi−κ×τ×f(ρi)的过程,使其达到收敛,简单的说就是使得求其 ∇ F ( ρ i ) ∇F(ρ_i) ∇F(ρi)最终为0,则使得目标函数收敛。

关于迭代式子 ρ i + 1 = ρ i − κ × τ × f ( ρ i ) ρ_{i+1}=ρ_i-\kappa\times\tau\times f(ρ_i) ρi+1=ρi−κ×τ×f(ρi)中的超参数 k 、 τ k、\tau k、τ ,在此处的公式为如下<注意,在不同的目标函数和约束条件下的 k 、 τ k、\tau k、τ一定是不同的,需要结合具体优化的算法(如此处的SDEA算法的目标函数)公式进行优化求解>
可行方向 f ( ρ i ) f(ρ_i) f(ρi)定义为
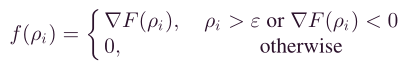
其中, τ \tau τ表示为
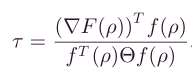
以上就是可行梯度方向法的基本思想了,如有描述不清,欢迎三连+骚扰啦!
❤坚持读Paper,坚持做笔记,坚持学习❤!!!
⚡To Be No.1⚡⚡哈哈哈哈
⚡创作不易⚡,过路能❤关注、收藏、点个赞❤三连就最好不过了
ღ( ´・ᴗ・` )
❤
『
Miracles sometimes occur, but one has to work terribly for them.
』
文章来源: blog.csdn.net,作者:府学路18号车神,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/weixin_44333889/article/details/119936570
- 点赞
- 收藏
- 关注作者


评论(0)