今天算是⚡正式开学⚡了~
一年过得真快，这就研二了o(╥﹏╥)o
呜呜呜。。。怎么就开学了（我还没放假呢）.
❤更新一篇Blog打卡一下吧！❤
⚡新学期⚡，⚡新气象⚡，⚡新风貌⚡来迎接新挑战！！！
加油！！！

搜罗了很多正则化（Regularization）的解释，发现在不同的地方有着不同的含义却又有着相似的味道。

下面，来细品！

定义

正则化(regularization)，是指在线性代数理论中，不适定问题通常是由一组线性代数方程定义的，而且这组方程组通常来源于有着很大的条件数的不适定反问题。大条件数意味着舍入误差或其它误差会严重地影响问题的结果。（来源自网络）

正则化：代数几何中的一个概念。

通俗定义

给平面不可约代数曲线以某种形式的全纯参数表示。

即对于$P{C}^2$中的不可约代数曲线$C$，寻找一个紧Riemann面$C\ast$和一个全纯映射$\sigma :C\ast \to P{C}^2$,使得$\sigma (C\ast )=C$.

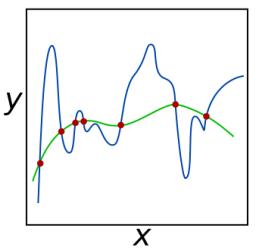
如上图为一个平面，为不可约代数曲线，用纯参数的多项式来表示此曲线，有点像线性回归，但又没有线性回归做的那么好。为什么取图片中的红色点呢，看下面的广义定义。

严格定义

设C是不可约平面代数曲线，S是C的奇点的集合。如果存在紧Riemann面C及全纯映射σ:C→PC^2,使得

1. σ(C*)=C
2. σ^(-1)
3. (S)是有限点集 (3) σ:C*\σ^(-1)(S)→C\S是一对一的映射

则称(C*,σ)为C的正则化。不至于混淆的时候，也可以称C*为C的正则化。

正则化的做法，实际上是在不可约平面代数曲线的奇点处，把具有不同切线的曲线分支分开，从而消除这种奇异性。

上面图中的红点，可看出奇点，如图可知，奇点处于曲线中单调的线上，前后则是局部极值。
从数学角度来说,所谓奇异性就是指函数的不连续或导数不存在,表现出奇异性的点称为奇异点。而此处则表现为导数不存在的情况。则为了消除这种奇异性，而提出了正则化的方法。

解决的问题

1. 正则化就是对最小化经验误差函数上加约束，这样的约束可以解释为先验知识(正则化参数等价于对参数引入先验分布)。约束有引导作用，在优化误差函数的时候倾向于选择满足约束的梯度减少的方向，使最终的解倾向于符合先验知识(如一般的l-norm先验，表示原问题更可能是比较简单的，这样的优化倾向于产生参数值量级小的解，一般对应于稀疏参数的平滑解)。
2. 同时，正则化解决了逆问题的不适定性，产生的解是存在，唯一同时也依赖于数据的，噪声对不适定的影响就弱，解就不会过拟合，而且如果先验(正则化)合适，则解就倾向于是符合真解(更不会过拟合了)，即使训练集中彼此间不相关的样本数很少。
3. 由于加了正则化项，原来不可逆的Hessian矩阵也变的可逆了。

深入拓展

提到正则化，现在一般都会联想到机器学习。

在Machine Learning（下面都用简称ML）中， 若参数过多，模型过于复杂，则会容易造成过拟合（overfitting）。即模型在训练样本数据上表现的很好，但在实际测试样本上表现的较差，不具备良好的泛化能力。

解决方法： 为了避免过拟合，最常用的一种方法是使用正则化，例如 L1 和 L2 正则化。

通常，你会在ML的误差函数（损失函数）公式中发现会加上一个额外的带系数的项，则这种额外项主要有两种形式—${\ell }_1-norm和{\ell }_2-norm$，翻译为中文呢，也就是L1正则化和L2正则化，（再通俗一点学过数学和矩阵理论的都应该知道）L1范数和L2范数，形式其实就是范数形式。

L1、L2正则化

在SVM（支持向量机）中，会引入一个叫做软间隔的概念，简单来说就是，在假定训练样本在样本空间中是线性可分的，也即为存在一个超平面可将其不同类的样本给完全分离开来。

在现实中，很难确定合适的核函数使得训练样本在特征空间中线性可分，就算是可以找到这样一个核函数，但也不知道其可分的结果是否是由于过拟合造成的。

如下图，为了缓解这样的问题，则想了个办法，就算将约束项给扩大，但也不是扩大到将所有样本都能够正确的划分，如果是这样的话，这就是“硬间隔”的概念了。故“软间隔”只是允许某些样本可不需要满足约束条件，扩大到能包含一些重要的样本特征就足够了。

软间隔示意图，红色圈出了不满足约束的样本--图片源自《机器学习》周志华

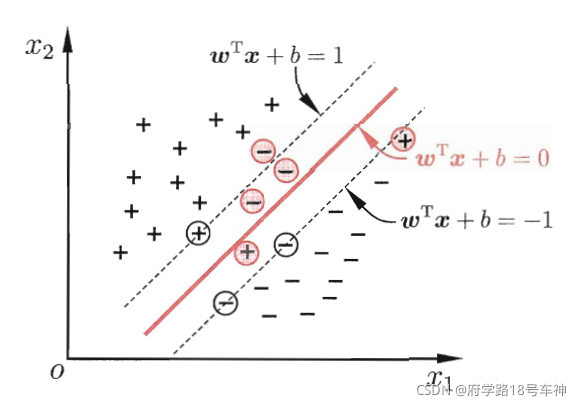
则会在优化的目标后面增加损失函数的惩罚项，如

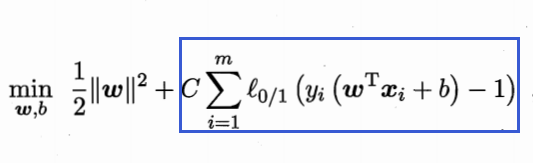
现在回到正则化中。

在上面的惩罚项中大体可看做为L1正则化（具体为0/1损失函数），使用L1正则化的模型建叫做Lasso回归，使用L2正则化的模型叫做Ridge回归（岭回归）。

像这样的，$\gamma ||v|{|}_1$则为L1正则化惩罚项，其中$\gamma$为惩罚系数，

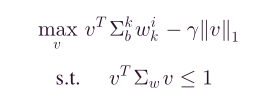
如下图，则为L2正则化，后面的$\alpha ||w_k|{|}_2^2$为惩罚项

从上面的L1和L2正则化项可看出，$v、w$是表示的一个投影向量。正则化项则对投影向量进行处理，也可理解为惩罚或限制约束等。

针对上面L1和L2正则化项进行解释：

1. L1正则化是指权值向量(投影向量) $v$ 中各个元素的绝对值之和，通常表示为$||v|{|}_1$。
2. L2正则化是指权值向量(投影向量) $w$ 中各个元素的平方和然后再求平方根（可以看到Ridge回归的L2正则化项有平方符号），通常表示为$||w|{|}_2$。

正则化的功能

关于正则化操作的意义或者说作用，大部分的Paper或者学者的理解：

1. L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择。
2. L2正则化可以防止模型过拟合（overfitting）；
   一定程度上，L1也可以防止过拟合。

关于稀疏权值矩阵，最开始我也很懵逼，从字面上也很难理解到其中的意义。

稀疏矩阵

简单来说，稀疏矩阵指的是很多元素为0，只有少数元素是非零值的矩阵，即得到的线性回归模型的大部分系数都是0。

此处引用一个很好的解释。

机器学习中特征数量很多，例如文本处理时，如果将一个词组（term）作为一个特征，那么特征数量会达到上万个（bigram）。在预测或分类时，那么多特征显然难以选择，但是如果代入这些特征得到的模型是一个稀疏模型，表示只有少数特征对这个模型有贡献，绝大部分特征是没有贡献的，或者贡献微小（因为它们前面的系数是0或者是很小的值，即使去掉对模型也没有什么影响），此时我们就可以只关注系数是非零值的特征。这就是稀疏模型与特征选择的关系。（源自网络）

这里让我想到了PCA的特征提取，通过对不同特征的贡献度不同来进行选择。生成稀疏权值矩阵的话，可以进一步的细化特征的选择。

关于L1、L2的直观理解可以看这位大佬的。

关于L1比L2正则化更容易获得稀疏解

从上面大佬的直观图解中其实也能看出点眉目，还是搬运一下下吧。

如下图，为L1正则化的，方框棱形则为L1正则化项函数，不难理解为啥为一个棱形（1范数$||v|{|}_1$，对v的绝对值，不完全可微）

L1正则化

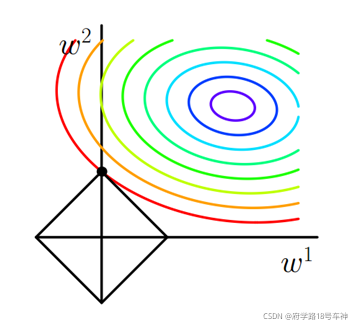
下图，为L2正则化，圆形则为L2正则化项函数，2范数$L=||w|{|}_2$可看成一个在原点的二次函数（二维情况下也就是一个圆）

L2正则化

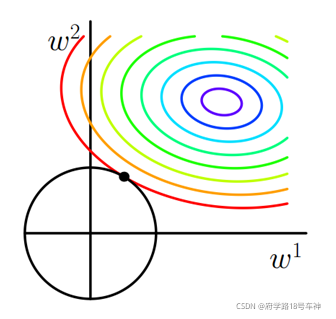
上图彩虹等高线则为原未加正则化项的优化目标函数$J$。

从直观的图中对比来看，两者正则化项与$J$相交的点则为最优解。但是为了得到稀疏权值解，则需要得到$w$为0的值，从图中看L2使得$w$的情况是及其困难，而L1与$J$相交的点大概率是在棱角尖尖位置处，此时可实现$w=0$的情况。

所以说，为了获得稀疏权值或者说稀疏解，我们在更好的选择是加上L1正则化惩罚项。

这里在知乎上有很多大佬也解释了为什么：L1 相比于 L2 为什么容易获得稀疏解？

可以参考参考哦~

❤坚持读Paper，坚持做笔记，坚持学习❤！！！
⚡To Be No.1

⚡⚡哈哈哈哈

---

⚡创作不易⚡，过路能❤关注、收藏、点个赞❤三连就最好不过了

ღ( ´･ᴗ･` )

❤

『
In delay there lies no plenty , Then come kiss me , sweet and twenty , Youth’s a stuff that will not endure .
』

文章来源: blog.csdn.net，作者：府学路18号车神，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/weixin_44333889/article/details/119945386