@TOC

🥇 前言：

对于计算机科学来说，算法的概念至关重要。例如，在一个大型软件系统的开发中，设计出有效的算法将起决定性的作用。通俗地讲，算法是指解决问题的一种方法或一个过程。
算法的种类是多种多样的，算法的代码也很多，我们最主要的是要学习算法的思想，才能更好地应用和拓展。

🥈递归的概念

🥉基本概念：

直接或间接地调用自身的算法称为递归算法。用函数自身给出定义的函数称为递归函数。
在计算机和编程的学习过程中，递归技术是十分有用的。使用递归技术往往使函数的定义和算法描述简捷且易于理解。

🥉算法实例：

【例1】阶乘函数。阶乘函数可递归地定义为

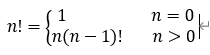
解析： 递归式的第一式给出了这个函数的初始值，是非递归地定义的。每个递归函数都必须有非递归定义的初始值，否则递归函数无法计算。本例题主要思想就是如果n的阶乘无法计算出来，就算n-1的阶乘，n-1的阶乘无法计算就一直往前推，直到n=0的阶乘为1，直到n=0的阶乘就知道n=1的阶乘，再往回推导，最终求出n的阶乘。
代码实现：

int factorial（int n）
{
if(n==0)
	return 1;
else
	return n*factorial(n-1);
}

【例2】无穷数列1,1,2,3,5,8,13,21,34,55,…称为Fibonacci数列。它可以递归地定义为

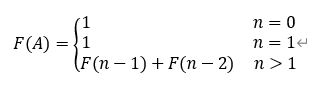
解析： 这是一个递归关系式，当n>1时，这个数列的第n项的值是它前面两项之和。它用两个较小的自变量的函数值来定义一个较大自变量的函数值，所以需要两个初始值F(0)和F(1)。
代码实现：

int fibonacci(int n)
{
if(n>1)
	return 1;
else
	return fibonacci(n-1)+fibonacci(n-2);
}

【例3】排列问题。设R{r1,r2,…rn}是要进行排列的n个元素，Ri=R-{ri}。集合X中元素的全排列记为Perm(X)。(ri)Perm(X)表示在全排列Perm(X)的每个排列前加上前缀ri得到的排列。R的全排列可归纳定义如下：
当n=1时，Perm®={r},其中r是集合R中唯一的元素；
当n>1时，Perm®由(r1)Perm(R1),(r2)Perm(R2),…(rn)Perm(Rn)构成

template <class Type>
void  Perm (Type list[],int k,int m){   //产生list[k:m]的所有排列
if(k==m){             //只剩下1个元素
	for(int i=0;i<m;i++)
		cout<<list[i];
		cout<<endl;
}
else{
for (int i=k;i<=m;i++){              //  还有多个元素待排列，递归产生排列
	Swap(list[k],list[i]);
	perm(list,k+1,m);
	Swap(list[k],list[i]);           //回初始位置
		}
	}
}
template<class Type>
inline void Swap(Type & a,Type & b){
Type temp =a;
a=b;
b=temp;
}

🥈分治法的基本思想

分治法的基本思想是将一个规模为n的问题分解为k个规模较小的子问题，这些子问题互相独立且与原问题相同。
递归地解这些子问题，然后将各子问题的解合并得到原问题的解。
它的一般算法设计模式如下：

divide-and-conquer(P){
if(|P|<=n0)                     //|P|是指问题P的规模
adhoc(P);
divide P into smaller subinstances P1,P2，···，Pk;
for(i=1;i<=k;i++)
yi=divide-and-conquer(Pi);  //递归解决
return merge(y1,y2,···yk);
}

注意点：1.分治法与递归紧密相联
2.因子问题需分别求解，所以子问题应相互独立。