思维导图整理大厂面试高频数组3: 两数之和II有序数组, 多个有序, 思路全变, 力扣167

此专栏文章是对力扣上算法题目各种方法的总结和归纳, 整理出最重要的思路和知识重点并以思维导图形式呈现, 当然也会加上我对导图的详解.

目的是为了更方便快捷的记忆和回忆算法重点(不用每次都重复看题解), 毕竟算法不是做了一遍就能完全记住的. 所以本文适合已经知道解题思路和方法, 想进一步加强理解和记忆的朋友, 并不适合第一次接触此题的朋友(可以根据题号先去力扣看看官方题解, 然后再看本文内容).

关于本专栏所有题目的目录链接, 刷算法题目的顺序/注意点/技巧, 以及思维导图源文件问题请点击此链接.

想进大厂, 刷算法是必不可少的, 欢迎和博主一起打卡刷力扣算法! 博主同步更新了算法视频讲解, 更易于理解, 不想看文章的 欢迎来看!

关注博主获得题解更新的最新消息!!!

题目链接: https://leetcode-cn.com/problems/two-sum-ii-input-array-is-sorted/

0.导图整理

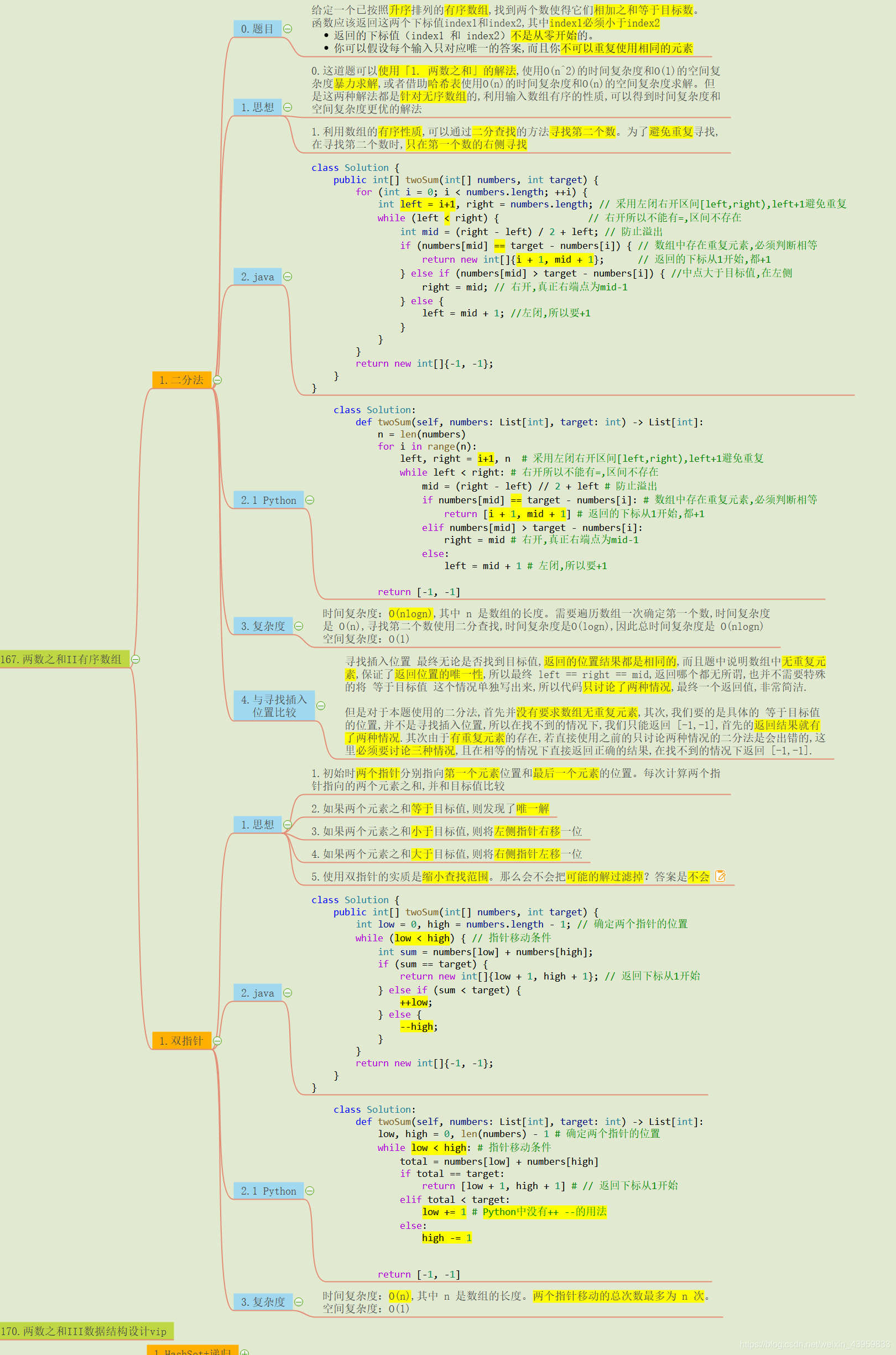
1.两数之和中有序和无序的区别

之前写了一篇关于无序数组的两数之和问题, 在无序数组中寻找第二个数就没有多少捷径, 毕竟数组无序, 很多经典的方法都用不上, 最后只能牺牲空间来换取时间, 利用哈希表将空间复杂度增加到了O(n), 从而降低了寻找第二个数的时间复杂度.

但是当数组有序之后, 就能使用一些经典的算法同时仍然保证空间复杂度为O(1), 不需要牺牲空间来换取时间, 比如下面马上介绍的 二分法 和 双指针 方法.

这里给我们提供了一种思维, 那我们是不是也可以将无序数组先进行排序后, 再使用这些经典算法呢? 当然可以这么做, 但对于两数之和来说, 必要性不是太大. 因为最快的排序算法也需要O(nlogn)的时间复杂度, 对于两数之和确实提升也不是太大, 但是对于 三数之和/四数之和 还是挺实用的, 后续文章将很快讲到.

2.二分法和寻找插入位置的区别

数组有序了, 使用二分法寻找第二个数就可以将时间复杂度降到O(logn)了, 关于二分法, 之前的这篇文章已经讲解的很清楚了, 这里就不再重复介绍了.

这里说说 二分法 和 寻找插入位置的不同, 也是两篇文章中代码不同的部分.

寻找插入位置 最终无论是否找到目标值, 返回的位置结果都是相同的, 而且题中说明数组中无重复元素, 保证了返回位置的唯一性, 所以最终 left == right == mid, 返回哪个都无所谓, 也并不需要特殊的将 等于目标值 这个情况单独写出来, 所以代码只讨论了两种情况, 最终一个返回值, 非常简洁.

但是对于本题使用的二分法, 首先并没有要求数组无重复元素, 其次, 我们要的是具体的 等于目标值 的位置, 并不是寻找插入位置, 所以在找不到的情况下, 我们只能返回 [-1, -1], 首先的返回结果就有了两种情况.

其次由于有重复元素的存在, 若直接使用之前的只讨论两种情况的二分法是会出错的, 这里必须要讨论三种情况, 且在相等的情况下直接返回正确的结果, 在找不到的情况下返回 [-1, -1].

本题另外的一个小的注意点是: 返回的下标从1开始, 只要在原本的返回结果上+1就可以了.

还有一个注意点是, 为了避免重复寻找,在寻找第二个数时,只在第一个数的右侧寻找, 也就是left = i+1.

3.双指针思想

双指针在有序数组中是非常重要的思想, 一定要掌握. 思想还是挺简单的, 但是优化的效果是非常棒的, 比二分法更加优秀. 导图中对思想的描述挺清楚了, 这里说下它的适用范围吧.

最基本最首要的前提是 数组一定要是有序的, 其次, 一定要涉及到几个数之间的相互关系, 最常用的也就是几个数相加等于某一定值的情况, 其他情况, 今后遇到了再细说. 常用于数组和链表之中.

源码

Python:

# 二分法
class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        n = len(numbers)
        for i in range(n):
            left, right = i+1, n  # 采用左闭右开区间[left,right),left+1避免重复
            while left < right: # 右开所以不能有=,区间不存在
                mid = (right - left) // 2 + left # 防止溢出
                if numbers[mid] == target - numbers[i]: # 数组中存在重复元素,必须判断相等
                    return [i + 1, mid + 1] # 返回的下标从1开始,都+1
                elif numbers[mid] > target - numbers[i]:
                    right = mid # 右开,真正右端点为mid-1
                else:
                    left = mid + 1 # 左闭,所以要+1
        
        return [-1, -1]

# 双指针
class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        low, high = 0, len(numbers) - 1 # 确定两个指针的位置
        while low < high: # 指针移动条件
            total = numbers[low] + numbers[high]
            if total == target:
                return [low + 1, high + 1] # // 返回下标从1开始
            elif total < target:
                low += 1 # Python中没有++ --的用法
            else:
                high -= 1


        return [-1, -1]

​

java:

// 二分法
class Solution {
    public int[] twoSum(int[] numbers, int target) {
        for (int i = 0; i < numbers.length; ++i) {
            int left = i+1, right = numbers.length; // 采用左闭右开区间[left,right),left+1避免重复
            while (left < right) {                // 右开所以不能有=,区间不存在
                int mid = (right - left) / 2 + left; // 防止溢出
                if (numbers[mid] == target - numbers[i]) { // 数组中存在重复元素,必须判断相等
                    return new int[]{i + 1, mid + 1};      // 返回的下标从1开始,都+1
                } else if (numbers[mid] > target - numbers[i]) { //中点大于目标值,在左侧
                    right = mid; // 右开,真正右端点为mid-1
                } else {
                    left = mid + 1; //左闭,所以要+1
                }
            }
        }
        return new int[]{-1, -1};
    }
}

// 双指针
class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int low = 0, high = numbers.length - 1; // 确定两个指针的位置
        while (low < high) { // 指针移动条件
            int sum = numbers[low] + numbers[high];
            if (sum == target) {
                return new int[]{low + 1, high + 1}; // 返回下标从1开始
            } else if (sum < target) {
                ++low;
            } else {
                --high;
            }
        }
        return new int[]{-1, -1};
    }
}

​