高楼翻译:并发用户数的估算方法(请仔细看译者注)
- 原文名:《Method for Estimating the Number of Concurrent Users》 2004年
- 原作者: Eric Man Wong
- 翻译:高楼
作者注:
之所以翻译这篇文章,是因为17年过去了。这里面的并发用户的计算公式还是有大量的人在不知道具体推导逻辑的情况下使用。并且还有人称之为“业界标准”、“经典公式”。
当我们在网上搜索并发估算时,也大都可以看到同样的内容复制来复制去。
这个文章在我进入性能行业的时候就已经看过了,并没有当成一回事,因为只是一种具体场景的说明推导。但是到现在,有很多人都忽视了推导过程,而在各种系统中加以使用。
这篇文章并不是说完全的错误,但远远没有达到“标准公式”的级别。
这是比较奇怪的行业状态。做性能培训的不断教新人这个公式,做性能的老人带新人也这样教过。
我觉得看过我文章的人应该不会有这样的错误思路了,我已经写过了,这个公式的局限和逻辑。
只是耐不住有其他不懂具体逻辑的人还在不断影响着更多的人。
所以,在这里,我把这篇文章完整地翻译下来。
后面我会再写一篇文章,来说明这个推导过程中的问题在哪里,以及如何做才正确。
- 原文下载链接: https://pan.baidu.com/s/1-rfEWzdO2DE5siutZbKuVA
- 密码: 87f3
1 简介
为了进行容量计划和性能管理,通常需要在实际投入生产之前估计系统的并发用户数,这是因为许多系统资源的消耗与并发用户数直接相关。以 Web 应用程序为例:内存使用率、CPU 使用率、服务器进程/线程数、数据库连接数和网络带宽使用率都是同时登录系统的用户数增加的函数。
尽管很重要,但是人们经常在没有充分理由的情况下通过直觉或疯狂的猜测来估计并发用户的数量。
在本文中,我们尝试引入一种简单的方法来从其他一些参数中得出并发用户数,这些参数可以更容易地估计和证明。
2 不能令人满意的方法
人们有时用来估计并发用户数的一种方法是假设它等于总用户数的一定百分比。这不是一个好方法(译者注:比如说二八原则),因为即使有时可以可靠地估计用户总数,但使用的百分比数字通常是一个没有道理的幻数。
应该指出的是,以上提到的百分比不能视为在一定时间内访问系统的用户百分比。在某些情况下,可以可靠地估计后面的数字。例如,如果我们知道每个用户每月仅一次使用一个特定系统,并且都是均匀地分布的,那么我们可以安全地预测在任何情况下使用该系统的用户所占的百分比,一天约为 3.3%(即 1/30)。
但是,仅此数字不能用于推断并发用户数。这是因为在同一天使用系统的用户不一定会同时使用它。一些用户可能会在早上使用它,而某些用户可能会在下午使用它。
我们将在下一节中看到一种更好的方法。
3 估计平均并发用户数的公式
我们首先定义并发用户数的含义。但是在我们这样做之前,必须首先澄清术语登录会话。
登录会话是由开始时间和结束时间定义的时间间隔。在开始时间和结束时间之间,将占用一个或多个系统资源。以需要用户身份验证的 Web 应用程序为例,登录会话从用户登录到系统时开始,到用户注销时结束。为每个登录会话创建一个用户会话(占用系统内存)。登录会话的长度是开始时间和结束时间之间的差。
现在,我们准备定义并发用户的概念。我们将同意将特定时刻的并发用户数定义为该时刻所属的登录会话数。在以下示例中对此进行了说明:

横轴是时间线。每个水平线段代表一个登录会话。由于时间t0
处的垂直线截取了三个登录会话,因此时间t0
处的并发用户数等于3。
让我们关注从0到任意时刻T的时间间隔。以下结果可以用数学方式证明:

或者,如果从时间 0 到 T 的登录会话总数等于 n,并且登录会话的平均长度等于 L,则
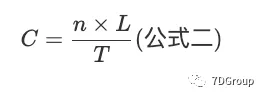
证明过程在附录中提供。直观地看,公式可以这样解释:假设代表登录会话的所有线段首尾相连,形成一个长字符串。如果字符串长于 T,那么我们必须将其绕一圈再缠绕几次,以将其填充到长度为 T 的空间中。必须缠绕字符串的次数类似于平均次数并发用户数。下图对此进行了说明:

4 估算参数
要使用第 3 节中的公式计算并发用户的平均数(C),先决条件是确定两个参数的值:
-
登录会话总数(n)。
-
在所关注的时间段长度(T)中,登录会话的平均长度(L)。
在本节中,我们提供有关如何估计这些参数的一些建议。
首先应该指出,公式中的 C 只是一个平均值。在相关时间段内,并发用户数可能会大幅波动。因此,如果我们希望 C 的值尽可能具有代表性,则应限制关注的时间段,以使新登录会话的到达率(即 n / T 之比)在该时间内或多或少稳定。例如,如果我们知道系统仅在办公时间内使用,则应将关注时间限制在办公时间内,而不是整天。因此,T 的值等于 8(假设是8小时工作)而不是24。否则,由于非工作时间未使用系统,C 的值将大大降低。
登录会话的总数(n)和登录会话的平均长度(L)通常可以由用户数量和使用习惯确定。例如,如果有 N 个潜在用户,并且我们知道用户一天使用一次,两次和三次使用系统的概率分别为 p1、p2、p3,且不会超过一天 3 次。则一天中的登录会话总数为 N( )。另一方面,可以通过观察用户样本如何使用系统来估计登录会话的平均长度。
在许多系统中,使用频率和登录会话的平均长度对于不同的用户而言差异很大。在这种情况下,如果我们可以将相似使用习惯的用户分为少量类别,则仍然可以进行上述分析。然后,我们可以计算每个类别的并发用户数,并将结果相加。
不可否认,用户的使用习惯通常很难准确预测。但是对于大多数系统,尤其是内部应用程序,通常可以得到一些合理的粗略数字。下一节提供了一个示例来说明这一点。
5 一个例子
H 市政府将为其 170,000 名员工启动电子工资系统,以查看他们自己的工资信息。由于 IT 能力水平各不相同,服务器的可用性有限以及检查薪资信息的其他方式的存在,据估计,当整个政府系统全面启动该系统时,只有 50% 的员工会定期使用该系统。在这些用户中,据估计还有 70% 的用户将在每月的最后一周内使用一次该系统。从参加 UAT 的用户观察到,平均使用时间约为 5 分钟。
现在,我们可以估算一个月的最后一周内的平均并发用户数。让我们将关注时间限制为任何一天的办公时间(上午9点至下午5点)。

因此,可以预测,在每个月的最后一周,平均将有大约 124 个并发用户访问该系统。
6 估计并发用户的高峰数量
6.1 理论
第3节中的公式估计了并发用户的平均数量。人们可能会问的下一个问题是:关于峰值我们能说什么?在本节中,我们将显示在某些假设下,还可以估计并发用户的峰值数量。
泊松概率分布是最常见、使用最广泛的统计工具,用于对时间上随机和独立事件的到达速度进行建模(可以在大多数入门级统计教科书中找到)。假设新登录会话的到达率具有平均值为λ的泊松分布,则根据定义:

其中 P 表示概率,e 是欧拉数,x!是 x 的阶乘。
在此假设下,可以证明任何时刻的并发用户数也具有泊松分布。最令人惊讶的结果是,无论登录会话长度的概率分布如何(登录会话的长度也是随机的,并且可以取一系列不同的值),它的确是真实的。用等式的形式可以表示如下:

其中 C 是在第3节中我们使用公式计算得出的平均并发用户数。(证明非常复杂且冗长。本文跳过了该证明。)
众所周知,平均值为C的泊松分布可以通过平均值为C且标准偏差为
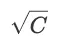
的正态分布来近似。(同样,它可以在大多数入门级统计教科书中找到。)。如果我们要表示 X 并发用户,这意味着
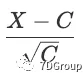
具有标准正态分布C,且平均值= 0,标准差=1。在正态分布标准表中查找数值,我们得到以下结果:
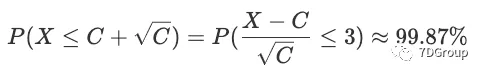
简而言之,上述等式意味着并发用户数小于
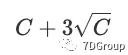
的概率为99.87%。在大多数情况下,该概率足够大,我们可以通过
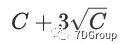
近似估算并发用户的峰值数量:
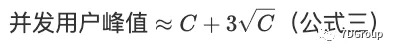
6.2 实践
在上一节中,我们显示了在新登录会话的到达具有泊松分布的假设下,可以估计并发用户的峰值数量。但是,对于许多实际应用程序,登录会话的到达都经历以下状态:
- 睡眠状态-在非办公时间没有登录会话;
- 临时状态(上升)-办公时间开始;人们开始登录系统;登录会话的到达率正在增加;
- 稳定状态–登录会话的到达速率变得稳定;
- 暂时状态(下降)–办公时间即将结束;人们正在离开系统;登录会话的到达率正在下降;
状态4之后是状态1,并且循环重复进行。
对于此类应用,第6.1节的假设仅对于状态3是合理的-即生命周期的稳定状态。因此,如果我们想更准确地预测并发用户的峰值数量,则应遵循以下步骤:
- 根据经验估算出稳定状态的时间段。
- 估计稳定状态下的登录会话数。
- 使用第3节的公式二计算并发用户C的平均数量。
- 应用第6.1节中的公式三计算并发的峰值数用户。
以上步骤将在第5节中以示例的方式再次说明,如下所示:
作为该示例的继续,进一步假设尽管工作时间为8小时,但仍然有80%的用户在9:30 am至12:30 am和2:30 pm至4:30 pm的5个小时内访问工资系统。同样,在这些时期中,新的登录会话的到来是稳定的。

读者可能会注意到,在第5节中计算出的平均并发用户数与上述计算出的平均值之间存在差异。实际上,它们都是有效数字。这示例说明了在第4节开始时所说的话,也就是说,并发用户的平均值可能在很大程度上取决于所关注的时间段。在第5节中,我们关注的时间段是整个工作时间,因此平均值在较少的人使用系统的情况下会被短的时间段拖累。在本节中,我们将关注的时间段仅限制在高峰时间,因此该值较大。尽管两个值均有效,但后一个数字可能是系统使用情况的更好表示。
7 从并发用户数中得出其他有用的属性
一旦发现并发用户数,便可以从中得出一些其他有用的系统属性。在本节中,我们将讨论请求速率的计算和网络带宽利用率。
对于 Web 应用程序,请求率(即每单位时间的请求数,有时称为命中率)是容量规划的另一个重要因素。如果可以从用户样本中确定每个用户的平均请求率为r,那么很容易看到:

其中

分别是并发用户的平均数和峰值。
以薪资系统为例,如果每个用户平均每分钟发出 10 个请求,则高峰时段的平均总请求速率约为 。
同样,如果我们可以确定单个用户的平均网络带宽利用率,则可以以类似方式计算总网络带宽利用率。单个用户的网络带宽利用率是指单位时间通过网络从系统传输到用户的位数/字节数。令每个用户的平均利用率为 u,则

8 总结
在本文中,我们提出了一个公式,用于根据关注时间段内登录会话的总数和登录会话的平均长度来计算系统的平均用户并发数量。已经给出了有关这些参数估计的一些建议。
在登录会话的到达具有泊松分布的假设下,我们还推导出了并发用户峰值的近似上限。
最后,我们展示了如何从我们估计的并发用户的平均数和峰值数中得出请求率和网络带宽利用率。
本文提出的公式并不是解决并发用户数问题的神奇解决方案。它们只是提供解决问题的方向。公式的准确性在很大程度上取决于估算一段时间内登录会话数的能力以及登录会话的平均长度,而这又取决于用户的行为和使用方式。这些有时很难准确预测,并且也消耗成本。但是,我们认为,对于许多应用程序,可以以相对较低的成本获得一些粗略而合理的估计。
附录:第 3 节中的公式证明(公式一)
令
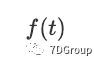
为时间 t 的并发用户数。想象一下,从 0 到 T 的时间段被分成 n 个等间隔的子间隔。每个间隔的长度为:
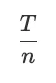
。并且第 i 个间隔在

处结束,对于 :
当n取很大的值时,可以将平均并发用户数设为近似为:
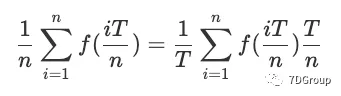
我们将定义从 0 到 T 的时间段内的平均并发用户数,作为上述求和值的平均取值,因为 n 趋于无穷大。求和就成为了积分。因此,
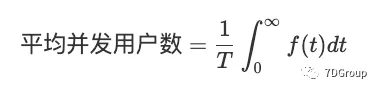
假设在 0 到 T 的时间内有 m 个登录会话,并且这些登录会话的编号从 1 到 m。令第 i个登录会话的开始时间和结束时间分别为

我们将函数

与第 i 个登录会话关联,其定义为:

下图说明了该函数的定义:

然后,以下等式直接根据第 3 节开头给出的并发用户数的定义得出:
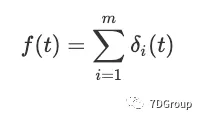
从 0 到 T 的两边进行积分
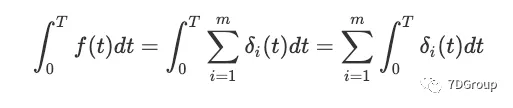
(t) 是函数 $δi(t) $下的面积,显然等于上图的
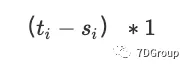
它仅等于第 i 个登录会话的长度。
因此,
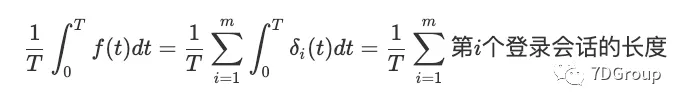
因此证明了公式一。
9 最后
通读了这个文章之后,你可以思考下几个问题:
- 是否可以用 login session 做为并发的计算基础数据?
- 公式 中推导时, 恒等于 1 或恒等于 0,是否合理?
- 公式 中推导时,如何判断函数两边是否可积?
- 函数
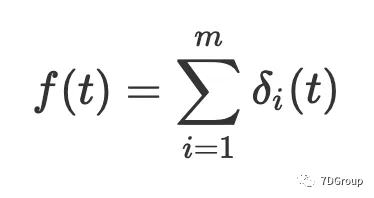
是否可积分?如果考虑因为系统资源导致的不连续性?
- 对应附录中的推导过程,在实际应用时,如何考虑积分的闭区间和有界?
- 如何理解

等于第 i 个登录会话的长度? - 对应第 4 节,如何获取你系统中的具有业务含义的会话总数?
- 在 6.1 节,请注意 “假设新登录会话的到达率具有平均值为 λ 的泊松分布” 这一句。当应用到自己的系统中时,如何确定请求到达的分布特征?
- 泊松分布近似到正态标准分布的过程过滤掉了什么真实的业务场景?
- 根据正态分布标准表查找的 C+3* 根号 C 是否可以应用到你的特定业务场景?
- 根据“公式的准确性在很大程度上取决于估算一段时间内登录会话数的能力以及登录会话的平均长度,而这又取决于用户的行为和使用方式。这些有时很难准确预测,并且也消耗成本。”这一段,你如何获取用户的行为和使用方式?
- 点赞
- 收藏
- 关注作者

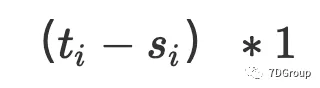

评论(0)