🌊 作者主页：海拥
🌊 简介：🏆CSDN全栈领域优质创作者、🥇HDZ核心组成员、🥈蝉联C站周榜前十
🌊 粉丝福利：粉丝群 每周送6~9本书，不定期送各种小礼品，往期获奖公布

概 念

认证(Authentication)：即鉴别、确认，它是证实某事是否名副其实，或是否有效的一个过程。

认证与加密的区别：

• 加密用以确保数据的保密性，阻止对手的被动攻击，如截取、窃听。
• 认证用以确保报文发送者和接受者的真实性以及原文的完整性，阻止对手的主动攻击，如冒充、篡改、重播等。

认证往往是应用系统中安全保护的第一道防线，极为重要（确保用户的合法性）。

MAC函数与加密函数的区别

• MAC函数与加密函数类似，都需要明文、密钥和算法的参与。
• 但MAC算法不要求可逆性，而加密算法必须是可逆的。
• 例如：使用100比特的消息和10比特的MAC，那么总共有2^100^个不同的消息，但仅有2^10^个不同的MAC。也就是说，平均每2^90个消息使用的MAC是相同的。
• 因此，认证函数比加密函数更不易被攻破，因为即便攻破也无法验证其正确性。关键就在于加密函数是一对一的，而认证函数是多对一的。

MD5的算法框图

输入消息可任意长，压缩后输出为128bits。

算法步骤(1)－分组填充

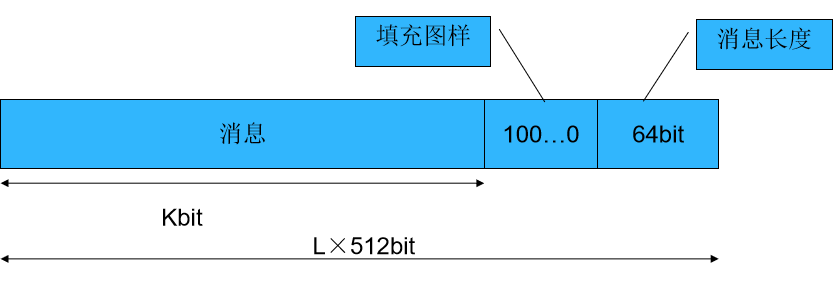
• 如果消息长度大于2^64^，则取其对2^64^的模。
• 执行完后，消息的长度为512的倍数（设为L倍），则可将消息表示为分组长为512的一系列分组Y0，Y1，…，YL~-1~，而每一分组又可表示为16个32比特长的字，这样消息中的总字数为N=L×16，因此消息又可按字表示为M[0,…,N~-1~]。

算法步骤(2)－缓冲区初始化

hash函数的中间结果和最终结果保存于128位的缓冲区中，缓冲区用32位的寄存器表示。可用4个32bits字表示：A, B, C, D。初始存数以十六进制表示为

A=01234567
B=89ABCDEF
C=FEDCBA98
D=76543210

算法步骤(3) -H~MD5~运算

• 以分组为单位对消息进行处理每一分组Yq(q=0,…,L~-1~)都经一压缩函数HMD5处理。HMD5是算法的核心，其中又有4轮处理过程。
• H~MD5~的4轮处理过程结构一样，但所用的逻辑函数不同，分别表示为F、G、H、I。每轮的输入为当前处理的消息分组Yq和缓冲区的当前值A、B、C、D，输出仍放在缓冲区中以产生新的A、B、C、D。
• 每轮又要进行16步迭代运算，4轮共需64步完成。
• 第四轮的输出与第一轮的输入相加得到最后的输出。
  
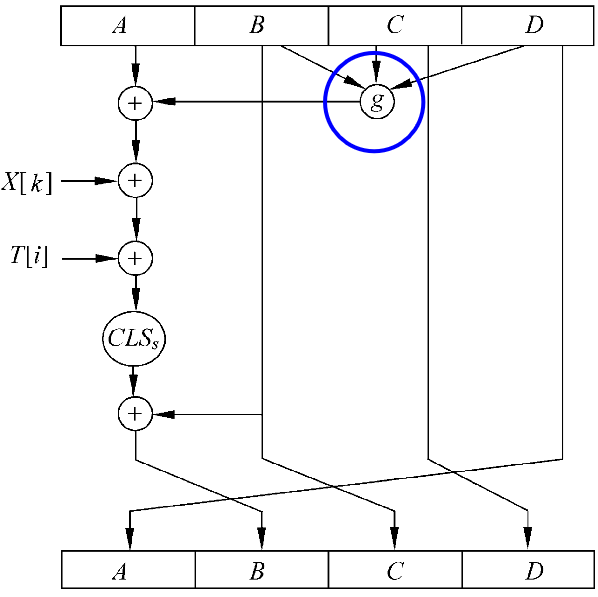
  压缩函数中的一步迭代
  

基本逻辑函数定义

压缩函数中的一步迭代

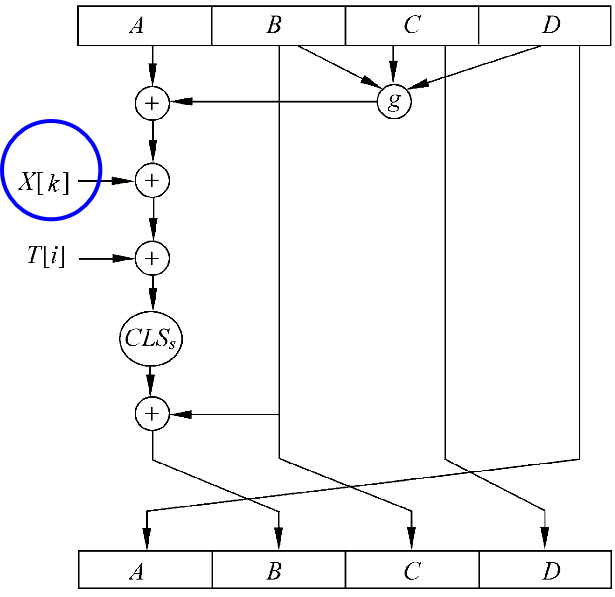
X[k]当前分组的第k个32位的字。

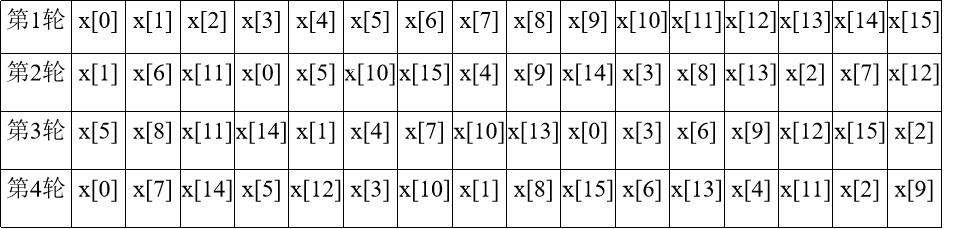
压缩函数中的一步迭代

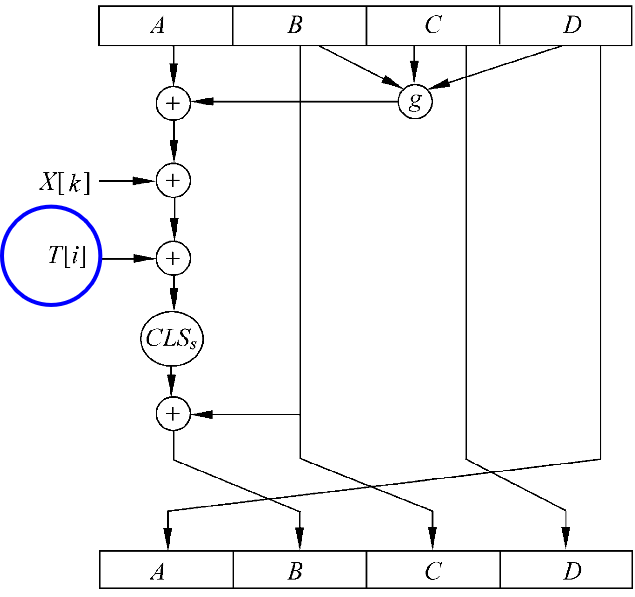
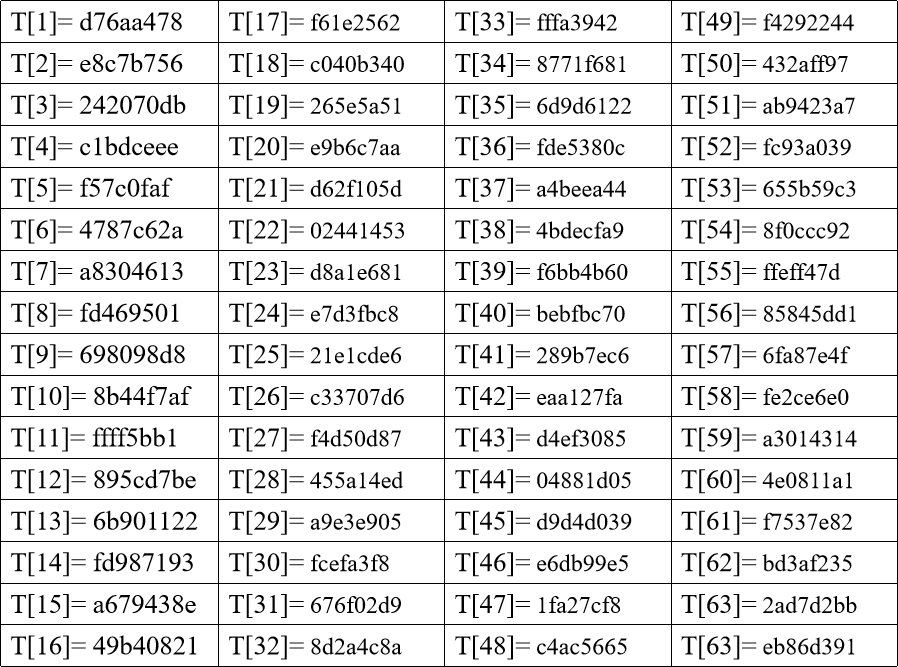
T[i]

T[1,…,64]为64个元素表，分四组参与不同轮的计算。T[i] = 2^32^×abs(Sin(i))的整数部分，i是弧度。T[i]可用32 bit二元数表示，其目的就是参与计算消除输入数据的规律性。

压缩函数中的一步迭代

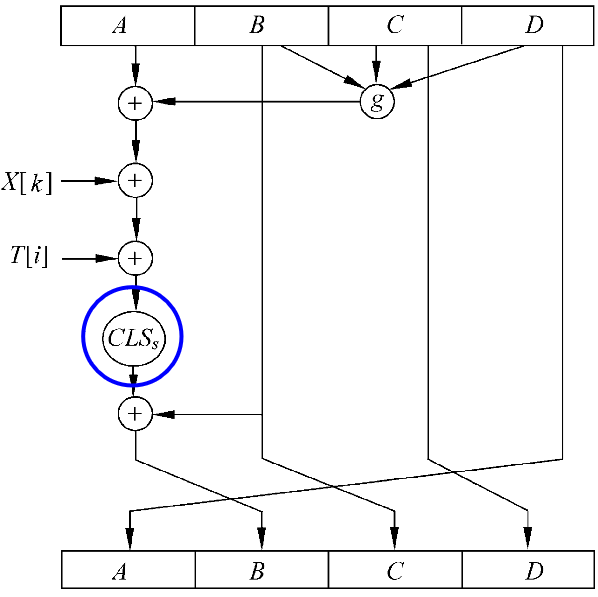
CLS~s~ ：循环左移s位

第一轮：7、12、17、22
第二轮：5、 9、14、20
第三轮：4、11、16、23
第四轮：6、10、15、21

算法描述

消息填充：与MD5完全相同
附加消息长度：64bit长度
缓冲区初始化
A＝67452301
B＝EFCDAB89
C＝98BADCFB
D＝10325476
E＝C3D2E1F0

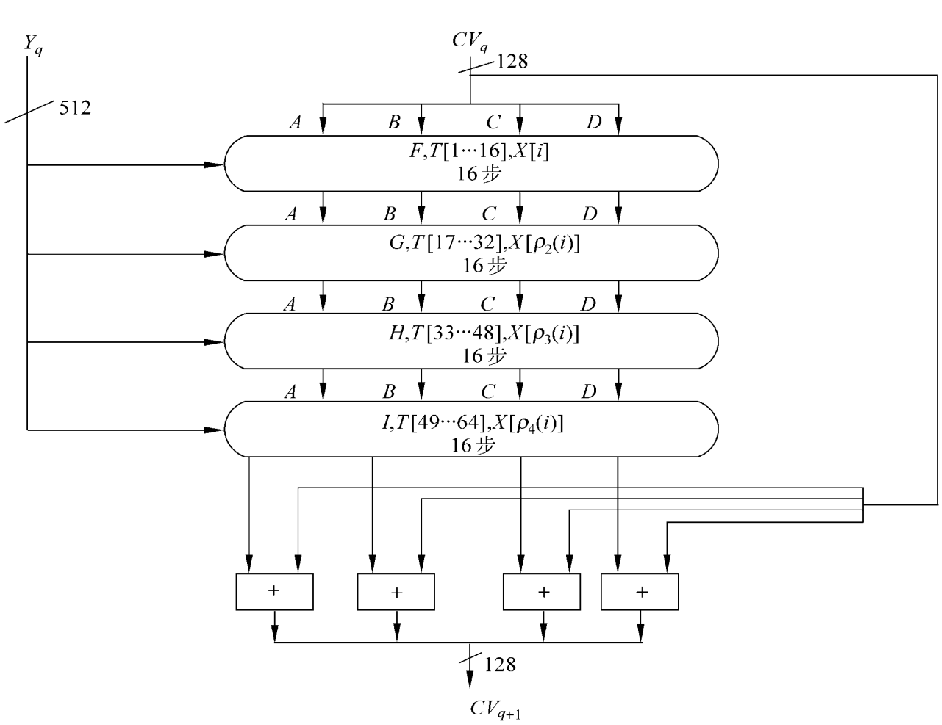
分组处理

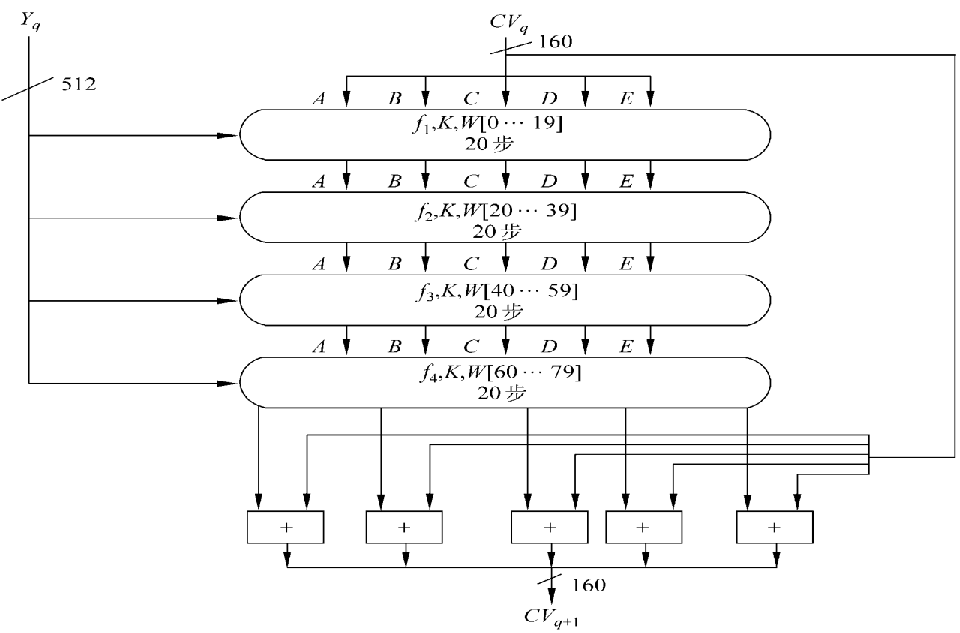
SHA-1压缩函数（单步）

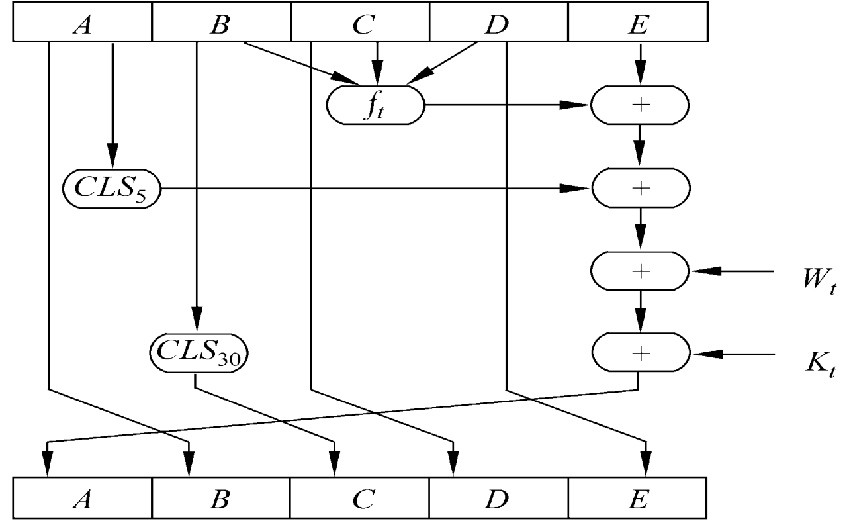
ft ----基本逻辑函数

SHA-1压缩函数（单步）

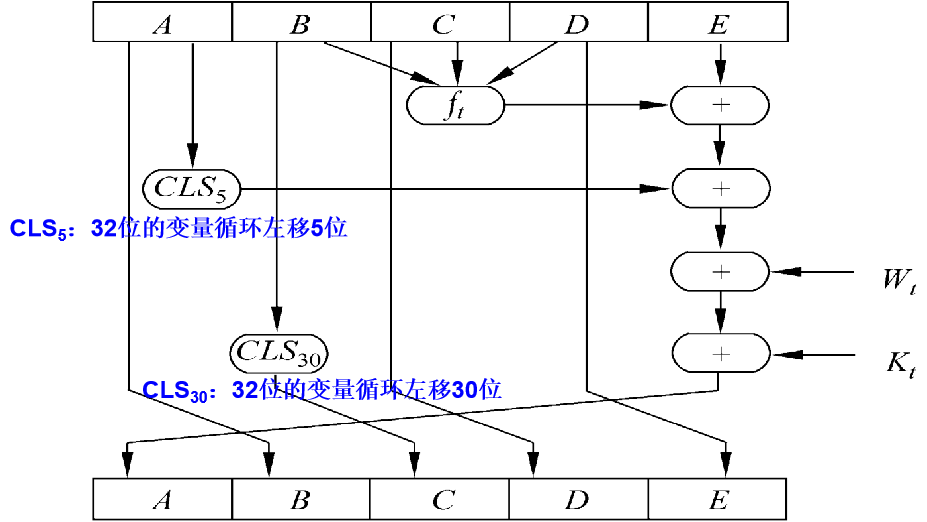
Wt —从当前512位输入分组导出的32位字

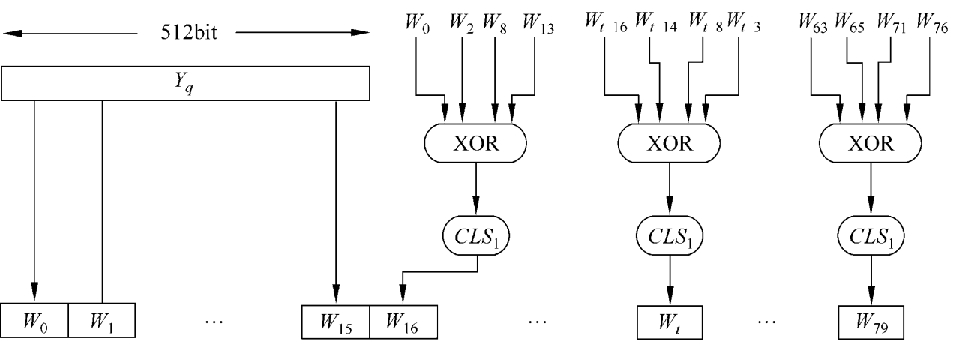
前16个值（即W~0~,W~1~,…,W~15~）直接取为输入分组的16个相应的字，其余值（即W~16~,W~17~,…,W~79~）取为

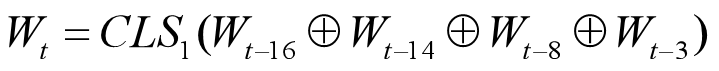
Kt —加法常量