一阶RC高通滤波器详解（仿真+matlab+C语言实现）

如果本文帮到了你，帮忙点个赞；
如果本文帮到了你，帮忙点个赞；
如果本文帮到了你，帮忙点个赞；

HPF 一阶RC高通滤波器详解（仿真+matlab+C语言实现）
LPF 一阶RC低通滤波器详解（仿真+matlab+C语言实现）

预备知识

高通滤波器（HPF-high pass filter）可以滤除频率低于截止频率的信号，类似的还有低通滤波器，带通滤波器，带阻滤波器。一阶RC高通滤波器的电路如下图所示；

关于电容

首先对电容的几个公式做一下补充；
电容大小$C$满足；
$$C=\frac{q}{V}\cdots ①$$
其中 $q$ 是电容所带的电荷量，$V$ 是电容两端的电势差；
另外，电流相当于单位时间流过导体的电荷量；因此电流 $i$ 满足；
$$i=\frac{dq}{dt}\cdots ②$$

根据①，②可以得到电容大小 $C$ 和电容的电流 $i$ 以及两端电压 $V$ 的关系；
$$i(t)=C\frac{dv(t)}{dt}$$

HPF的推导

由以上电路可知，假设电流为 $i(t)$，则可知
{ V o u t = R i ( t ) ⋯ ③ i ( t ) = C d Q c ( t ) d t ⋯ ④

所以结合①，③，④可以得到；
$$Q_c(t)=C(V_{in}(t)-V_{out}(t))\cdots ⑤$$

根据 ③，④，⑤ 可以得到以下关系；
$$V_{out}=\stackrel{I(t)}{\overbrace{C(\frac{d{V}_{in}}{dt}-\frac{d{V}_{out}}{dt})}}R=RC(\frac{d{V}_{in}}{dt}-\frac{d{V}_{out}}{dt})\cdots ⑥$$

将方程进行离散化，如果输入$V_{in}$和输出输入$V_{out}$按照 ${△}_T$的时间采样，那么可以将输入和输出序列化，则
$V_{in}$序列化为：
$$(x_1,x_2,x_3\cdots ,x_{n-1},x_n)$$
$V_{out}$序列化为：
$$(y_1,y_2,y_3\cdots ,y_{n-1},y_n)$$

根据⑥式可以进行离散化，因此最终滤波输出的序列 $y_i$ 如下所示；
$$y_i=RC(\frac{x_i-x_{i-1}}{{△}_T}-\frac{y_i-y_{i-1}}{{△}_T})\cdots ⑦$$
将⑦再进一步简化得到；

$$y_i=\alpha y_{i-1}+\alpha (x_i-x_{i-1})$$

其中 $\alpha =\frac{RC}{RC+{△}_T}$

所以换成得到；
$$RC={△}_T(\frac{\alpha }{1-\alpha })\cdots ⑧$$

另外截止频率和低通滤波器的相同；
$$f_c=\frac{1}{2\pi RC}$$

将⑧式代入可以得到截止频率和 $\alpha$ 的关系；
$$f_c=\frac{1-\alpha }{2\pi \alpha {△}_T}$$
这个公式便于简化后面程序以及截止频率的计算。

simulink 仿真

这里根据公式⑥构建simulink的子模块subsystem；
$$V_{out}=RC(\frac{d{V}_{in}}{dt}-\frac{d{V}_{out}}{dt})$$
具体如下所示；

整体的仿真如下图所示；

其中Sine Wave频率设置为2*pi*40，频率为40赫兹;

其中Sine Wave1频率设置为2*pi*4，频率为4赫兹;

所以这里需要使得2*pi*4的信号衰减，所以根据，截止频率 $f_c$ 的计算公式，可以改变增益的值，具体如下所示；

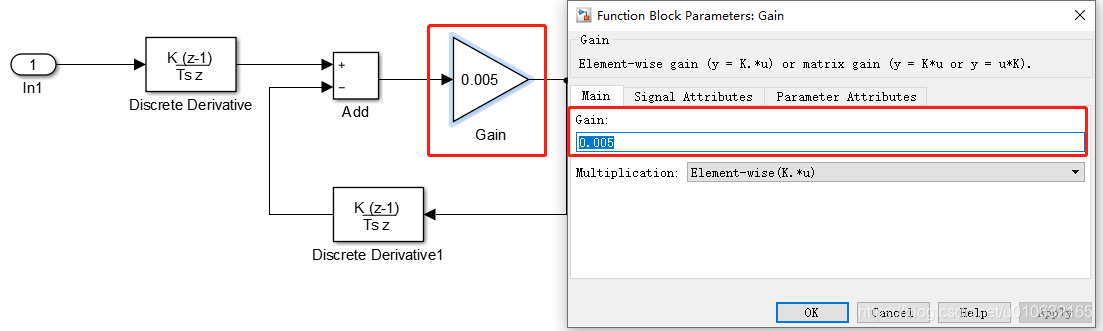
这里RC增益为0.005，因此
$f_c=\frac{1}{2\pi RC}=\frac{1}{2\pi \ast 0.005}\approx 31.8$

simulink 运行结果

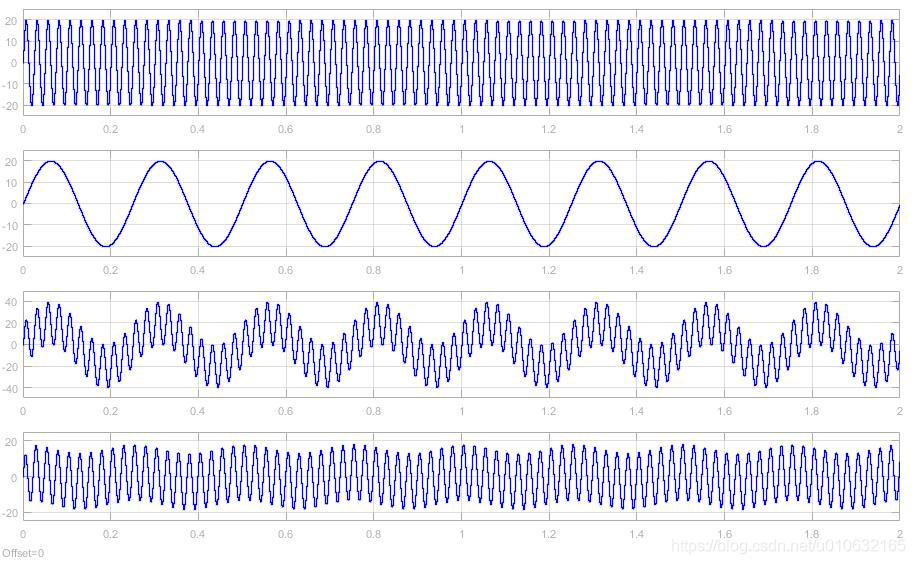
matlab 实现

matlab根据以下这个公式进行数字滤波器的设计；
$$y_i=\alpha y_{i-1}+\alpha (x_i-x_{i-1})$$
另外 $\alpha$ 的值如何确定需要参考⑧式；

Serial = 0:0.1:100;
Fs = 1;
Phase = 0;
Amp = 1;

N0 = 2*pi*Fs*Serial - Phase;
X0 = Amp*sin(N0);
subplot(4,1,1);
plot(X0);

Fs = 0.02;
N1 = 2*pi*Fs*Serial - Phase;
X1 = Amp*sin(N1);
subplot(4,1,2);
plot(X1);

X2=X0+X1;
subplot(4,1,3);
plot(X2);

len = length(X2);
X3=X2;
p=0.75;

for i=2:len
    X3(i) = p*X3(i-1)+p*(X2(i)- X2(i-1))
end

subplot(4,1,4);
plot(X3);

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
 

简单地分析一下，代码中的X1，X2，X3；

• X1频率为1
• X2频率为0.02

{ α = p = 0.75 △ T = 0.1 f c = 1 − α 2 π α △ T

因此可以得到截止频率如下；
$$f_c=\frac{0.25}{2\pi \ast 0.75\ast 0.1}\approx 0.53$$

matlab 运行结果

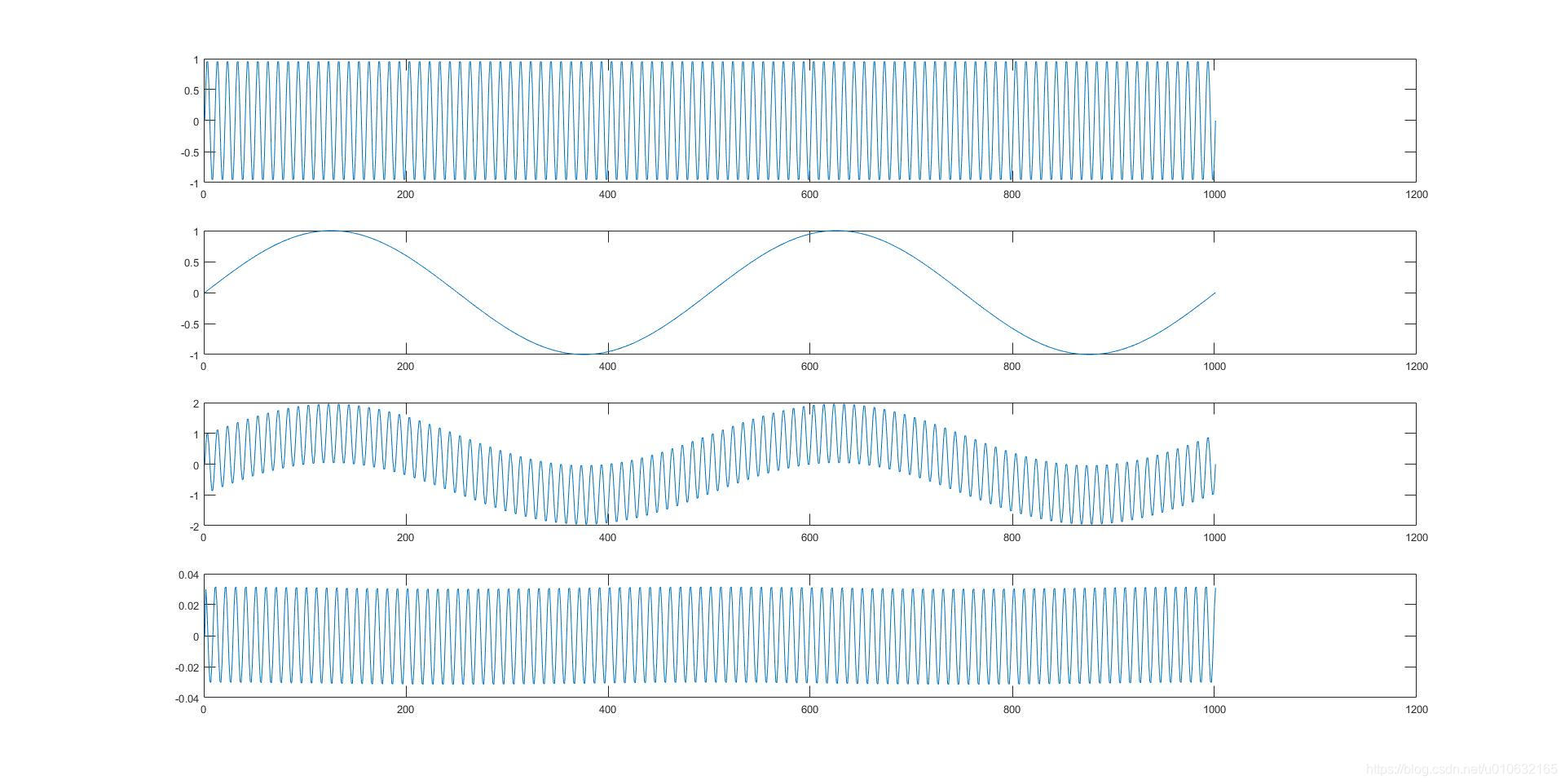
C语言实现

typedef struct
{
     int16_t  Input[2];
     int16_t  Output[2];
     int32_t  FilterTf;		
     int32_t  FilterTs;
     int32_t  Ky;
} high_filter;

void high_filter_init(high_filter *v);
int16_t high_filter_calc(high_filter *v);

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
 

其中；

• FilterTs为采样时间 ${△}_T$；
• FilterTf为RC时间常数；
• Input[0]表示 $x_i$；
• Input[1]表示 $x_{i-1}$；
• Output[0]表示 $y_i$；
• Output[1]表示 $y_{i-1}$；
• Ky表示$\frac{RC}{RC+{△}_T}$；

参考公式如下所示；

void high_filter_init(high_filter *v){	
     v->Ky = v->FilterTf*1024/(v->FilterTs + v->FilterTf);
}

int16_t high_filter_calc(high_filter *v){

	int32_t tmp = 0;

	tmp = ((int32_t)v->Ky*v->Output[1] + v->Ky*(v->Input[0] - v->Input[1]))/1024;
	if(tmp>32767){
		tmp = 32767;
	}
	
	if( tmp < -32768){
		tmp = -32768;
	}
	
    v->Output[0] = (int16_t)tmp;
    v->Output[1] = v->Output[0];
    v->Input[1] = v->Input[0];
	return v->Output[0];
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
 

文章来源: great.blog.csdn.net，作者：小麦大叔，版权归原作者所有，如需转载，请联系作者。

原文链接：great.blog.csdn.net/article/details/104218639