手把手教你快速排序算法,看看它到底有多快?
快排有多快
说到快我只推崇葵花宝典,那叫一个快啊~~~

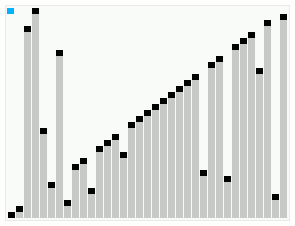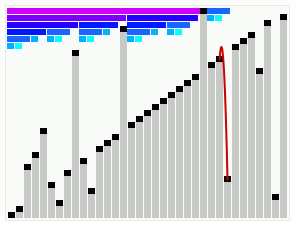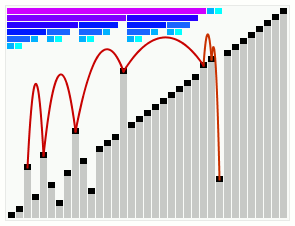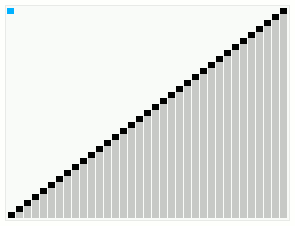
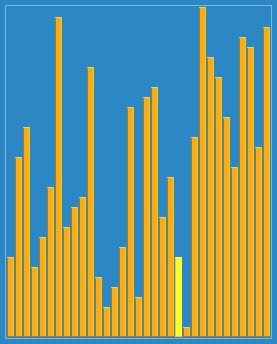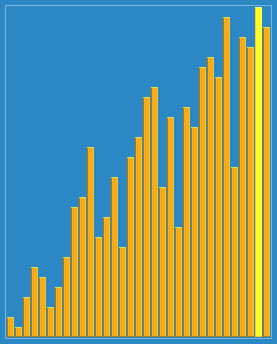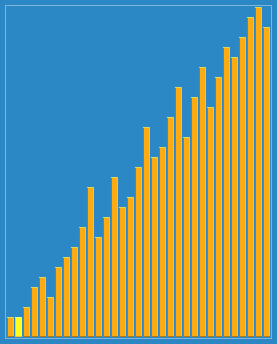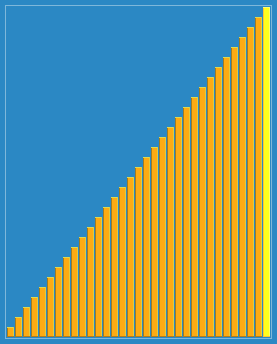
皮一下哈哈,言归正传。快速排序算法如其名一样,快!来看看快排和其他几大排序算法的并行运行对比视频(中间那个就是快排),你就知道它到底有多快了,请全屏横屏播放更清晰:
啥是快排?
分治思想
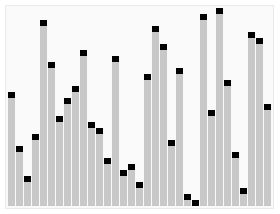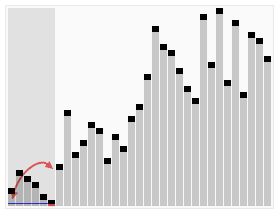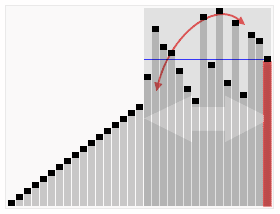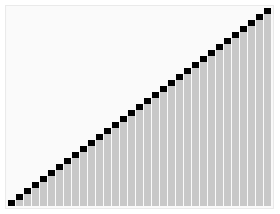
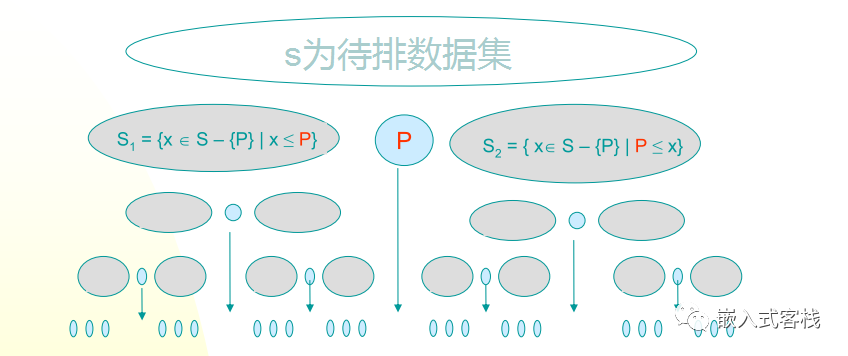
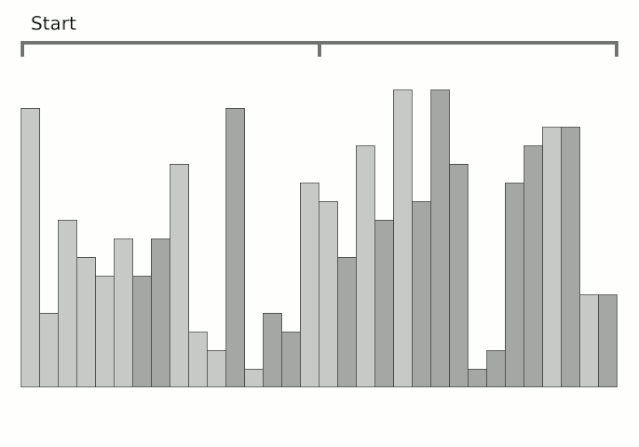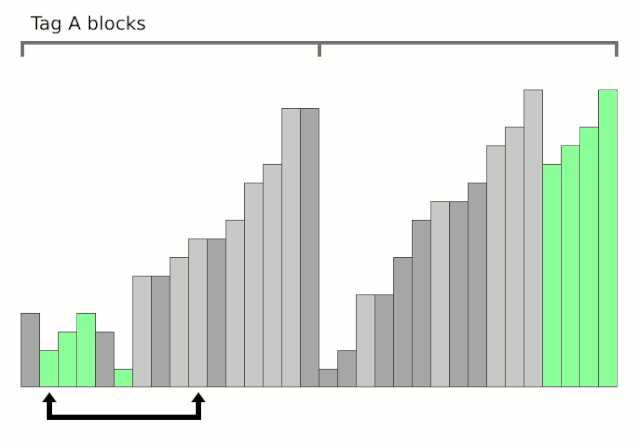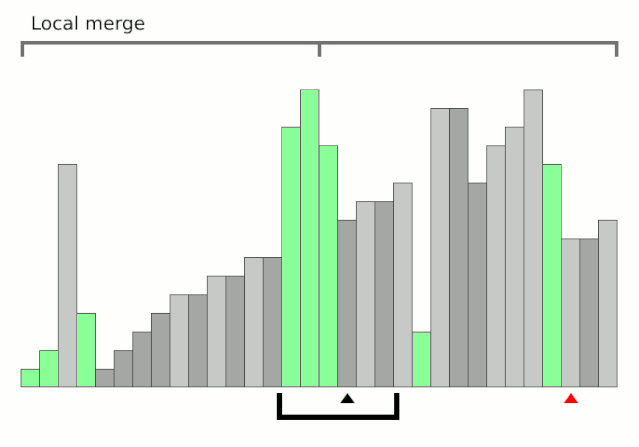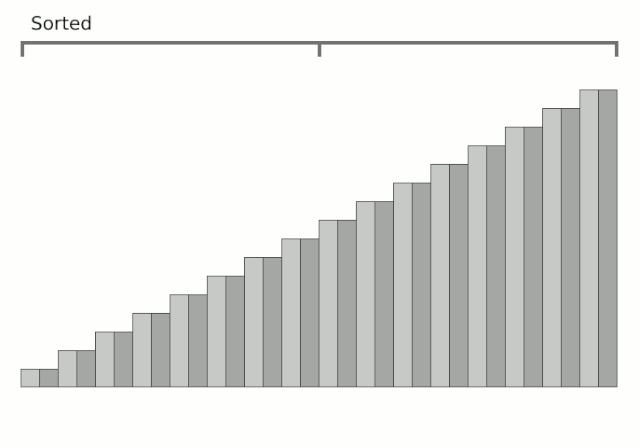
从待排元素集中选取一个元素作为摆动基准pivot,pivot这词比较形象,如上图像一个轴一样在摆动。记为P
将元素重新排列为3个子块:
左子块S1:由 P的元素组成
中间块M:仅有P一个元素
右子块S2:由≥P的元素组成
对左子块S1和右子块S2递归地重复上述过程,Return {quicksort(S 1 ), P, quicksort(S 2 )}.

代码实现
代码如下:
-
typedef int T_ELEMENT;
-
int partition(T_ELEMENT A[ ], int left, int right);
-
/* sort A[left..right] */
-
void quicksort(T_ELEMENT A[ ], int left, int right)
-
{
-
int q;
-
if( right <= left )
-
return;
-
if ( right > left )
-
{
-
q = partition(A, left, right);
-
/* partition分块后 */
-
//-> A[left..q-1] ≤ A[q] ≤ A[q+1..right]
-
quicksort(A, left, q-1);
-
quicksort(A, q+1, right);
-
}
-
}
-
-
int partition(T_ELEMENT A[], int left, int right);
-
{
-
T_ELEMENT P = A[left];
-
i = left;
-
j = right + 1;
-
/*无限循环,使用break退出*/
-
for(;;)
-
{
-
while (A[++i] < P) if (i >= right) break;
-
/* 此时 A[i] ≥ P */
-
while (A[--j] > P) if (j <= left) break;
-
/* 此时 A[j] ≤ P */
-
if (i >= j ) break; /*退出for循环*/
-
else swap(A[i], A[j]);
-
}
-
if (j == left) return j ;
-
swap(A[left], A[j]);
-
return j;
-
}
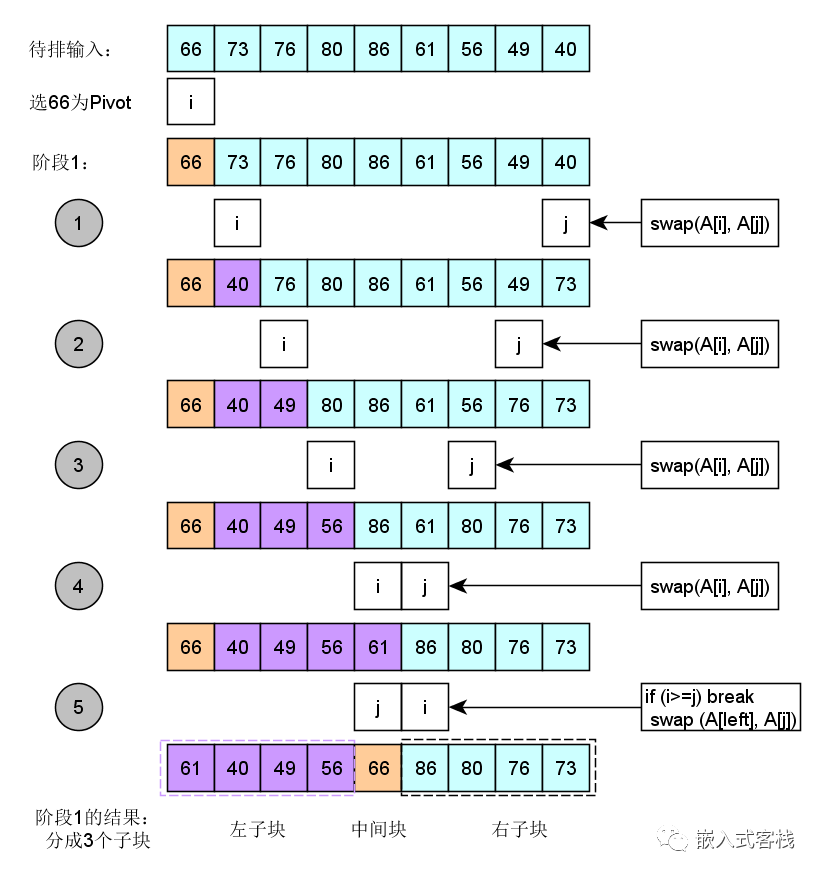
举栗子分析:

分成三块了,再递归子块迭代,直到right<=left. 这里放一个全过程慢镜头动图,帮助理解:

算法分析
这种快速排序的优点是我们可以“就地”排序,即无需依赖于输入大小的临时缓冲区。没有缓冲区内存开销,仅有栈开销。(注还有一种非递归的栈实现版本,本文就先不聊了)
partition步骤:时间复杂度为θ(n)。
快速排序涉及分区和2个递归调用。故:
T(n) = θ(n) + T(i) + T(n-i-1) = cn+ T(i) + T(n-i-1)
其中,i是分区后第一个子块的大小,将T(0)=T(1)= 1作为初始条件。
具体运行时间对不同特性的待排数据,其结果差异比较大,来看一下最好、最坏以及平均情况分析。
最差情况
当待排数据序列为正序或者逆序时,pivot将是在大小为n的待排块时中的最小(或最大)元素时。则阶段1迭代中生成一个空子块、pivot,及一个大小(n-1)的子块,则时间复杂度为θ(n)
递归方程:
如果这种情况在每个分区中都重复发生,那么每个递归调用处理一个比前一个列表小1的列表。因此需要在达到大小为1的列表之前进行n - 1次嵌套调用。这意味着调用树是n - 1个嵌套调用的线性链。第i次调用需要做O(n-i)复杂度来进行分区,则
最好情况
如每次分区时枢轴(pivot)都能取到中间值,即每次分区后,将产生两个大小大致相等的子块,并且枢轴(pivot)元素处于中间值位置,需要做n次比较运算。
递归方程:
如前所说,如每次执行分区时,都能将列表分成两个几乎相等的两个子块。这意味着每次递归调用都要处理一个只有一半大小的列表。因此,在到达大小为1的列表之前,我们只能进行 嵌套调用。这意味着调用树的深度为 ,但是在调用树的同一级别上没有两个调用处理原始列表的相同部分;因此,每个级别的调用总共只需要O(n)个时间(每个调用都有一些固定的开销,但是由于每个级别上只有O(n)个调用,所以这被包含在O(n)因子中)。结果是,该算法只使用c(n log n)的时间。故时间复杂度为O(n log n)。
平均情况
要对n个不同元素的数组进行排序,快速排序需要O(n log n)的预期时间,推导很枯燥就不罗嗦了。
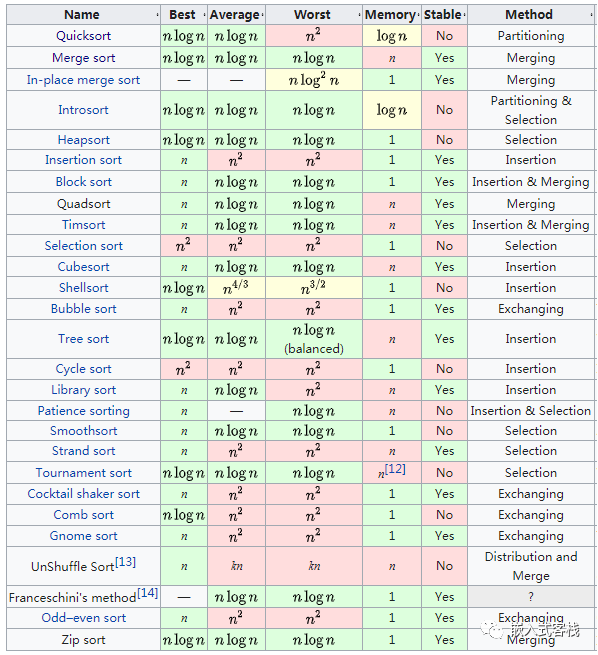
其他排序算法
图片来自wikipedia:

注:快排不需要额外的缓冲区开销,但是需要栈开销,其空间复杂度为O(log n).
这里对上表其中几个效率相对较高的做个简要介绍,后面如有机会再深入学习总结:
Introsort内省排序,在C++ STL中有应用。内省排序(英语:Introsort)是由David Musser在1997年设计的排序算法。这个排序算法首先从快速排序开始,当递归深度超过一定深度(深度为排序元素数量的对数值)后转为堆排序。采用这个方法,内省排序既能在常规数据集上实现快速排序的高性能,又能在最坏情况下仍保持O(n log n) 的时间复杂度。由于这两种算法都属于比较排序算法,所以内省排序也是一个比较排序算法。
Timsort排序算法:是一种混合稳定排序算法,它是从合并排序和插入排序中派生而来的,旨在对多种实际数据表现良好。由Tim Peters在2002年实现,用于Python编程语言。该算法查找已排序(运行)的数据的子序列,并使用它们对其余部分进行更有效的排序。这是通过合并运行直到满足特定条件来完成的。自2.3版以来,Timsort一直是Python的标准排序算法。还应用在Android平台上的Java SE 7、GNU Octave(是一个开源的类MATLAB数序软件)、V8(开源Java script引擎)以及Swift中,用于对非原始类型的数组进行排序。
MergeSort归并排序:在计算机科学中,是一种高效的,通用的,基于比较的排序算法。大多数实现产生稳定的排序,这意味着相等元素的顺序在输入和输出中是相同的。归并排序是约翰·冯·诺伊曼(John von Neumann)在1945年发明的分而治之算法。早在1948年,Goldstine和von Neumann的报告就对自下而上的合并排序进行了详细描述和分析。

Tournament sort:通过使用优先级队列来查找排序中的下一个元素,它改进了选择排序。在原始的选择排序中,需要O(n)个操作才能选择n个元素中的下一个元素;在锦标赛排序中,需要进行O(log n)运算(在O(n)中建立初始锦标赛之后)。锦标赛排序是堆排序的一种变体。
树形选择排序又称锦标赛排序(Tournament Sort):是一种按照锦标赛的思想进行选择排序的方法。首先对n个记录的关键字进行两两比较,然后在 个较小者之间再进行两两比较,如此重复,直至选出最小的记录为止。
块排序或块合并排序Block sort: 它将至少两个合并操作与插入排序组合在一起,以达到O(n log n)的位置稳定排序。合并两个排序的列表,A和B,等价于将A分成大小相等的块,在特殊规则下将每个块插入到B中,并合并AB对。

平滑排序smoothsort,是一种基于比较的排序算法。它是堆排序的一种变体,由Edsger Dijkstra于1981年发明并发布。它的时间复杂度上限是O(n log n),但它不是一个稳定的排序。平滑排序的优点是,如果输入已经排序到一定程度,那么它会更接近O(n)的时间,而堆排序的平均值是O(n log n),而不管初始排序状态如何。

希尔排序Shellsort,也称为Shell排序或Shell的方法,是一种就地比较排序。它可以被看作是交换排序(冒泡排序)或插入排序(插入排序)的泛化。该方法首先对彼此相距很远的元素对进行排序,然后逐步缩小要比较的元素之间的差距。通过从相隔很远的元素开始,它可以比简单的最近邻交换更快地将一些位置错误的元素移动到正确的位置。Donald Shell在1959年出版了第一个版本。Shellsort的运行时间很大程度上依赖于它使用的间隙序列。

算法应用
说到排序算法复杂度,请一定要与应用场景结合。主要需要考虑待排数据的集的尺寸,如果数据量小的时候反而是插入排序算法应用最为广泛;而对于海量数据场合,则应使用渐近有效排序策略。这是什么意思呢?说白了就是常使用混合算法!主要策略是利用快速排序、堆排序或归并排序将整体快速分治排序,同时对递归底部的小列表采用插入排序。事实上,在实际应用中有更复杂的变体,例如在Android,Java和Python中使用的Timsort(合并排序,插入排序和其他逻辑),以及在某些C++中用的introsort(快速排序和堆排序) 在.NET中排序实现。
再说白一点,在海量数据场景,利用快速排序、堆排序或归并排序将海量数据快速迭代成收敛的小块,而在小块中采用最为常见的插入排序尽快完成小块排序,小块中采用插入排序则可以更大程度减少递归深度。
总结一下
在信息时代,有海量信息需要处理,即便有非常强劲的处理器,但如没有很好的算法,仍然无法满足对这些信息的处理。在处理过程中,免不了要进行信息进行排序,快排在时空两个维度的开销都比较均衡,大量的应用软件、开发工具以及软件包都基于快排做了大量的应用。所以说快速排序改变世界,个人认为并不为过。同时对于求职面试,快速排序算法也是高频面试主题,值得深入研究掌握。
—— The End ——
推荐好文 点击蓝色字体即可跳转
欢迎转发、留言、点赞、分享给你的朋友,感谢您的支持!
分享 ???? 点赞 ???? 在看 ❤️
以“三连”行动支持优质内容!
-
文章来源: great.blog.csdn.net,作者:小麦大叔,版权归原作者所有,如需转载,请联系作者。
原文链接:great.blog.csdn.net/article/details/119881295
- 点赞
- 收藏
- 关注作者

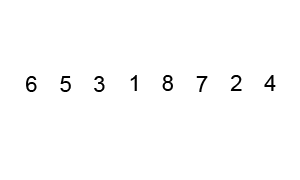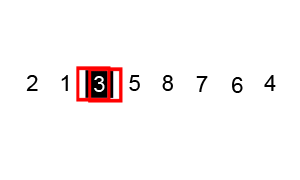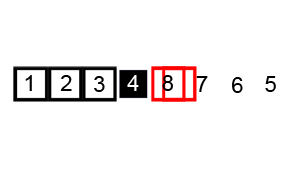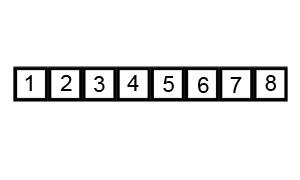
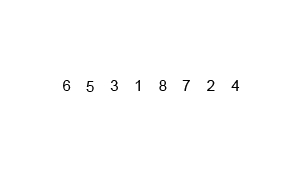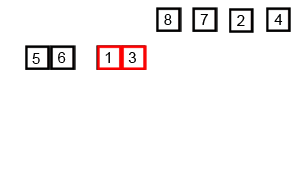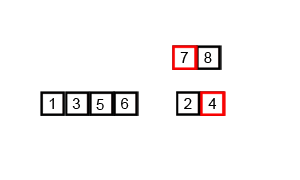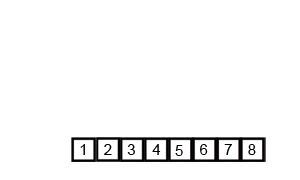


评论(0)