🌊 作者主页：海拥
🌊 简介：🏆CSDN全栈领域优质创作者、🥇HDZ核心组成员、🥈蝉联C站周榜前十
🌊 粉丝福利：粉丝群 每周送六本书，不定期送各种小礼品

@TOC

介绍

阅读本教程之前，建议您通读并理解我之前发的向量数学教程，因为本教程需要向量知识。

本教程介绍了转换以及如何使用矩阵在Godot中表示它们。它不是有关矩阵的完整深入指南。变换在大多数情况下都以平移，旋转和缩放的形式应用，因此我们将重点介绍如何用矩阵表示那些变换。

本指南大部分内容都使用Transform2D和 Vector2进行2D方面的研究，但是3D中的工作方式却非常相似。

==注意==

正如前面提到的教程，一定要记住，在陀，Y轴点是很重要的倒在2D。这与大多数学校教线性代数的方法相反，Y轴指向上方。

==注意==

约定是X轴为红色，Y轴为绿色，Z轴为蓝色。本教程使用颜色编码以匹配这些约定，但我们还将用蓝色表示原始矢量。

矩阵组件和恒等矩阵

单位矩阵表示没有平移，旋转和缩放的变换。让我们从身份矩阵及其组成与视觉外观的关系开始。

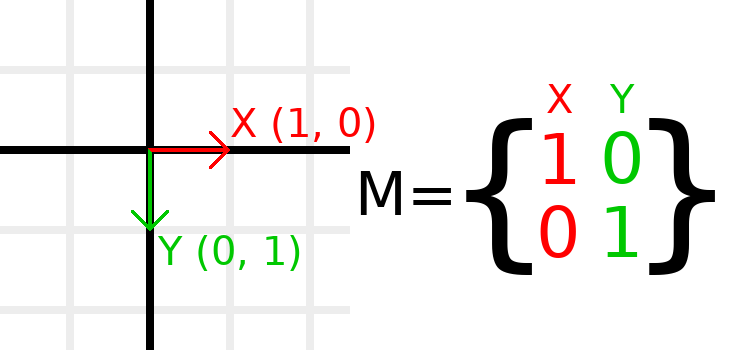
矩阵具有行和列，并且转换矩阵具有关于每个函数的特定约定。

在上图中，我们可以看到红色的X向量由矩阵的第一列表示，绿色的Y向量同样由第二列表示。更改列将更改这些向量。在接下来的几个示例中，我们将看到如何对其进行操作。

您不必担心直接操作行，因为我们通常使用列。但是，您可以将矩阵的行视为显示哪些向量有助于沿给定方向移动。

当我们引用诸如txy的值时，这就是X列向量的Y分量。换句话说，矩阵的左下角。同样，txx在左上方，tyx在右上方，tyy 在右下方，其中t是Transform2D。

缩放转换矩阵

应用比例尺是最容易理解的操作之一。首先，将Godot徽标放置在矢量下方，以便我们可以直观地看到对象上的效果：

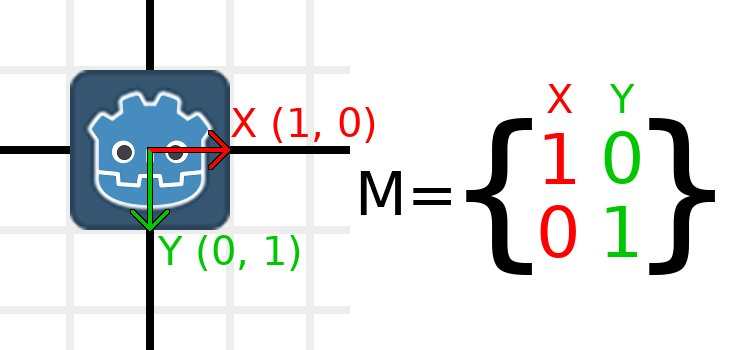
现在，要缩放矩阵，我们要做的就是将每个分量乘以所需的比例。让我们将其放大2。1乘2变为2，0乘2变为0，因此我们得出以下结论：

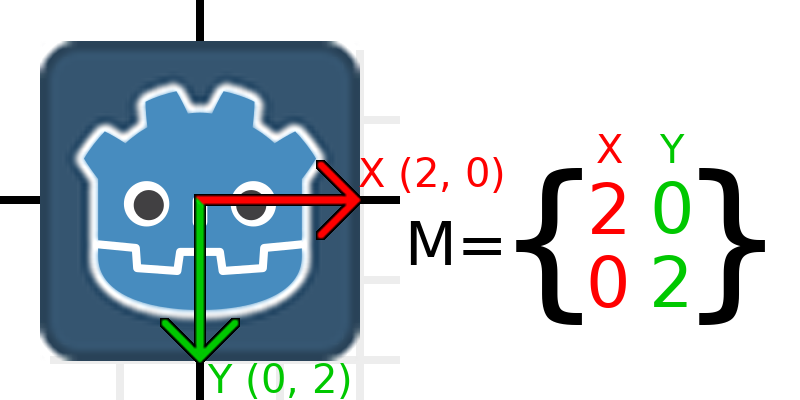
为此，我们可以简单地将每个向量相乘：

Transform2D t = Transform2D.Identity;
// Scale
t.x *= 2;
t.y *= 2;
Transform = t; //将节点的变换更改为我们刚刚计算的值。

如果我们想将其恢复为原始比例，可以将每个分量乘以0.5。缩放转换矩阵几乎就是所有这些。

要从现有的转换矩阵计算对象的比例，可以在每个列向量上使用length()。

==注意==

在实际的项目中，可以使用scaled()方法执行缩放。

旋转变换矩阵

我们将以与之前相同的方式开始，在身份矩阵下方添加Godot徽标：

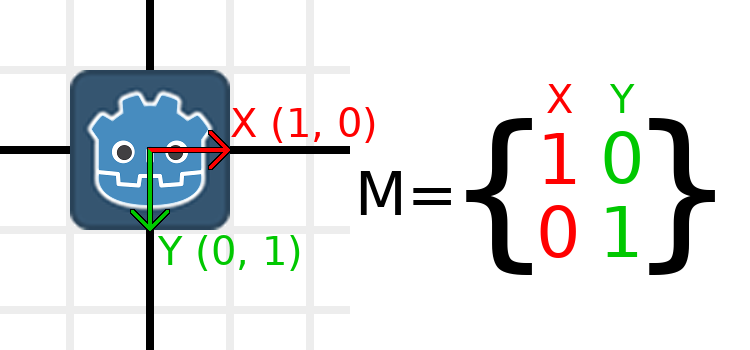
例如，假设我们要顺时针旋转Godot徽标90度。现在，X轴指向右侧，Y轴指向下方。如果我们在头部旋转这些按钮，则从逻辑上看，新的X轴应指向下方，新的Y轴应指向左侧。

您可以想象一下，您同时抓住了Godot徽标及其矢量，然后将其围绕中心旋转。无论您在哪里完成旋转，向量的方向都会确定矩阵是什么。

我们需要在法线坐标中表示“下”和“左”，所以这意味着我们将X设置为（0，1），将Y设置为（-1，0）。这些也是Vector2.DOWN和Vector2.LEFT的值。当我们这样做时，我们得到旋转对象的预期结果：

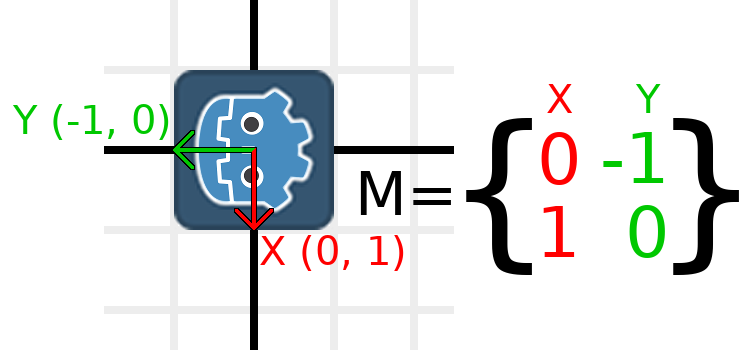
如果您在理解上述内容时遇到困难，请尝试以下练习：切一张纸，在其上方绘制X和Y向量，将其放在方格纸上，然后旋转并注意端点。

为了执行代码旋转，我们需要能够以编程方式计算值。此图显示了从旋转角度计算变换矩阵所需的公式。如果这部分看起来很复杂，请不要担心，我保证这是您需要了解的最难的事情。

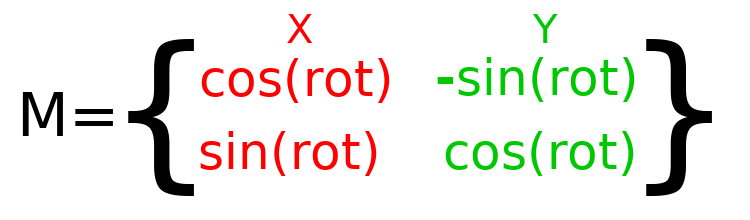
==注意==

Godot用弧度而不是度表示所有旋转。一整圈是TAU或PI * 2弧度，四分之一圈是TAU / 4或PI /
2弧度。使用TAU通常会使代码更具可读性。

==注意==

有趣的事实：除了Y在Godot中下降外，旋转还顺时针表示。这意味着所有数学和触发函数的行为都与Y-is-up
CCW系统相同，因为这些差异会“抵消”。您可以认为两个系统中的旋转都是“从X到Y”。

为了执行0.5弧度（约28.65度）的旋转，我们只需将0.5的值插入上面的公式并进行评估，以找出实际值应为：

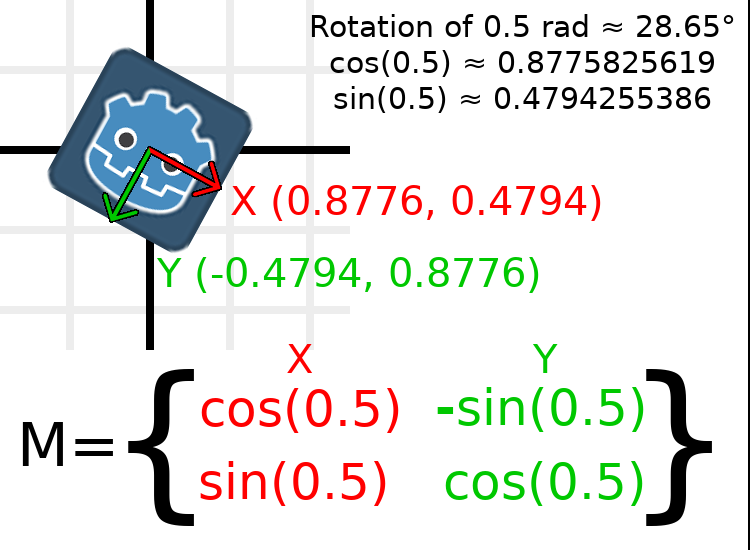
这是在代码中完成的方法（将脚本放置在Node2D上）：

float rot = 0.5f; // 要应用的旋转。
Transform2D t = Transform2D.Identity;
t.x.x = t.y.y = Mathf.Cos(rot);
t.x.y = t.y.x = Mathf.Sin(rot);
t.y.x *= -1;
Transform = t; // 将节点的变换更改为我们刚刚计算的值。

要从现有的变换矩阵计算对象的旋转，可以使用atan2（txy，txx），其中t是Transform2D。

==注意==

在实际项目中，可以使用 rotation （）方法执行旋转。

变换矩阵的基础

到目前为止，我们只使用了x和y向量，它们负责表示旋转，缩放和/或剪切（高级，最后进行了介绍）。X和Y向量一起称为变换矩阵的基础。术语“基础”和“基础向量”很重要。

您可能已经注意到，Transform2D实际上具有三个Vector2值：x，y和origin。该原点值不是基础的一部分，但它的变换一部分，我们需要它来表示位置。从现在开始，我们将在所有示例中跟踪原始向量。您可以将起源视为另一列，但通常最好将其完全分开。

请注意，在3D，陀有一个单独的基础保持三个结构的Vector3的基础值，因为代码可能会很复杂，它是有道理的把它从分离变换（这是由一个 基础和一个额外的Vector3的由来）。

翻译转换矩阵

更改原点向量称为转换变换矩阵。平移基本上是“移动”对象的技术术语，但是它显然不涉及任何旋转。

让我们通过一个示例来帮助理解这一点。我们将像上次一样从身份变换开始，不同的是这次我们将跟踪原始向量。

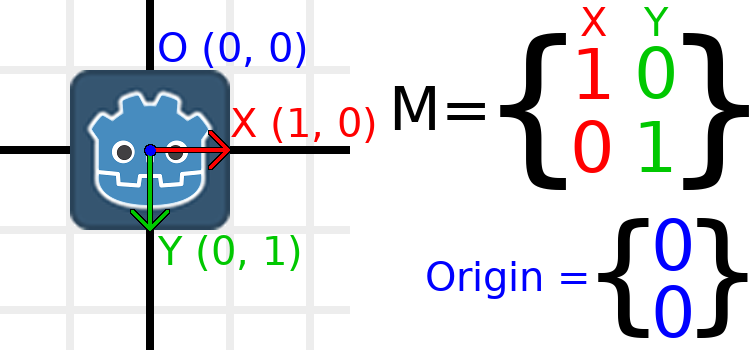
如果我们希望对象移动到（1，2）的位置，我们只需要将其原点矢量设置为（1，2）：

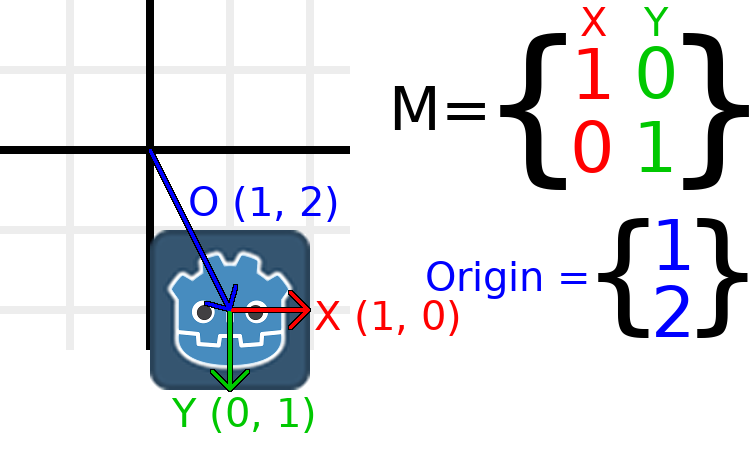
还有一个translation()方法，该方法执行与直接添加或更改原点不同的操作。该translation()方法将对象转换相对于其自身的旋转。例如，当使用Vector2.UP translation()时，顺时针旋转90度的对象将向右移动。

==注意==

Godot的2D使用基于像素的坐标，因此在实际项目中，您将需要以数百个单位进行平移。

全部放在一起

我们将把到目前为止提到的所有内容应用于一个转换。接下来，创建一个带有Sprite节点的简单项目，并使用Godot徽标作为纹理资源。

让我们将翻译设置为（350，150），旋转-0.5 rad，缩放3。我已经发布了屏幕截图，并提供了复制代码，但是我建议您尝试复制屏幕截图，而不用看码！

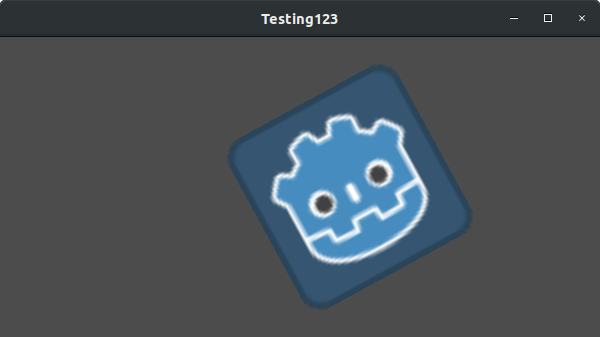
Transform2D t = Transform2D.Identity;
// Translation
t.origin = new Vector2(350, 150);
// Rotation
float rot = -0.5f; // 要应用的旋转。
t.x.x = t.y.y = Mathf.Cos(rot);
t.x.y = t.y.x = Mathf.Sin(rot);
t.y.x *= -1;
// Scale
t.x *= 3;
t.y *= 3;
Transform = t; // 将节点的变换更改为我们刚刚计算的值。

剪切变换矩阵（高级）

==注意==

如果您只是在寻找如何使用转换矩阵，请随时跳过本节。本节探讨了转换矩阵的一个不常用的方面，以建立对它们的理解。

您可能已经注意到，变换比上述动作的组合具有更大的自由度。2D变换矩阵的基础在两个Vector2值中具有四个总数，而旋转值和比例尺Vector2仅具有3个数。缺少自由度的高级概念称为剪切。

通常，您将始终使基本向量彼此垂直。但是，剪切在某些情况下可能很有用，了解剪切可以帮助您了解变换的工作方式。

为了直观地显示外观，让我们在Godot徽标上覆盖一个网格：

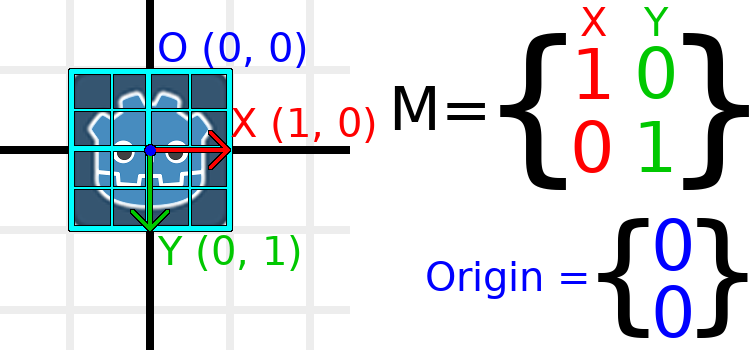
该网格上的每个点都是通过将基本向量相加而获得的。右下角是X + Y，而右上角是X-Y。如果更改基本矢量，则整个网格将随之移动，因为网格是由基本矢量组成的。无论我们对基本矢量进行什么更改，当前网格上所有平行的线都将保持平行。

例如，我们将Y设置为（1，1）：

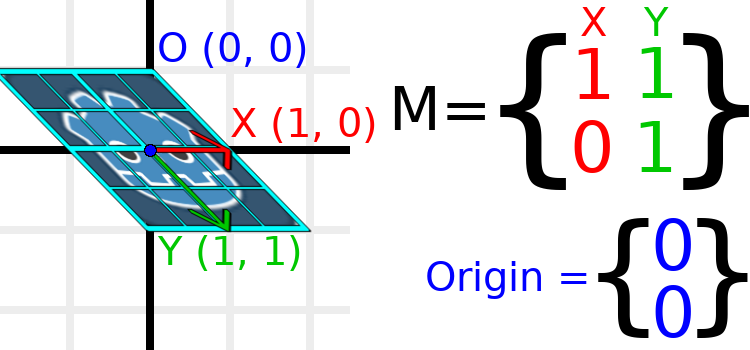
Transform2D t = Transform2D.Identity;
// 通过将 Y 设置为 (1, 1) 来剪切
t.y = Vector2.One;
Transform = t; //将节点的变换更改为我们刚刚的calculated.

==注意==

您无法在编辑器中设置Transform2D的原始值，因此，如果要剪切对象，则必须使用代码。

由于矢量不再垂直，因此已剪切了对象。网格的底部中心相对于其自身为（0，1），现在位于世界位置（1，1）。

对象内的坐标在纹理中称为UV坐标，因此在此我们借用该术语。为了从相对位置找到世界位置，公式为U * X + V * Y，其中U和V是数字，X和Y是基向量。

网格的右下角始终位于（1，1）的UV位置，位于（2，1）的世界位置，该位置由X * 1 + Y * 1计算得出，即（ 1，0）+（1，1）或（1 + 1，0 + 1）或（2，1）。这与我们对图像右下角位置的观察相符。

同样，网格的右上角始终位于（1，-1）的UV位置，位于（0，-1）的世界位置，该位置是根据X * 1 + Y *- 1，即（1，0）-（1，1）或（1-1，0-1）或（0，-1）。这与我们对图像右上角的位置的观察相符。

希望您现在完全理解了变换矩阵如何影响对象，以及基矢量之间的关系以及对象的“ UV”或“坐标内”如何改变其世界位置。

==注意==

在Godot中，所有变换数学都是相对于父节点完成的。当我们提到“世界位置”时，如果节点具有父级，则它将相对于节点的父级。

转换的实际应用

在实际项目中，通常将通过使多个Node2D或Spatial 节点彼此父代来处理转换中的转换。

但是，有时手动计算我们需要的值非常有用。我们将介绍如何使用Transform2D或 Transform手动计算节点的变换。

在转换之间转换位置

在许多情况下，您想在转换中进行位置转换。例如，如果您有一个相对于玩家的位置并想找到世界（父母相对）位置，或者您有一个世界位置并且想知道它相对于玩家的位置。

我们可以使用“ xform”方法找到相对于玩家的矢量在世界空间中的定义：

// 玩家下方 100 个单位的世界空间向量。
GD.Print(Transform.Xform(new Vector2(0, 100)));

我们可以使用“ xform_inv”方法来查找相对于玩家定义的世界空间位置：

// (0, 100) 相对于玩家在哪里？
GD.Print(Transform.XformInv(new Vector2(0, 100)));

==注意==

如果事先知道变换位于（0，0），则可以改用“ basis_xform”或“ basis_xform_inv”方法，这些方法将跳过翻译。

相对于自身移动对象

一种常见的操作（尤其是在3D游戏中）是相对于自身移动对象。例如，在第一人称射击游戏中，您希望当按时角色向前移动（-Z轴）W。

由于基本向量是相对于父对象的方向，而原点向量是相对于父对象的位置，因此我们可以简单地添加多个基本向量来相对于自身移动对象。

此代码将一个对象向右移动100个单位：

Transform2D t = Transform;
t.origin += t.x * 100;
Transform = t;

要在3D中移动，您需要将“ x”替换为“ basis.x”。

==注意==

在实际项目中，您可以在3D中使用translate_object_local或在2D中使用move_local_x和move_local_y。

将变换应用于变换

关于转换最重要的事情之一是如何一起使用其中的几个转换。父节点的变换会影响其所有子节点。让我们剖析一个例子。

在此图像中，子节点在组件名称之后带有“ 2”，以将其与父节点区分开。这么多的数字可能看起来有点让人不知所措，但是请记住，每个数字显示两次（在箭头旁边以及在矩阵中），并且几乎有一半的数字为零。

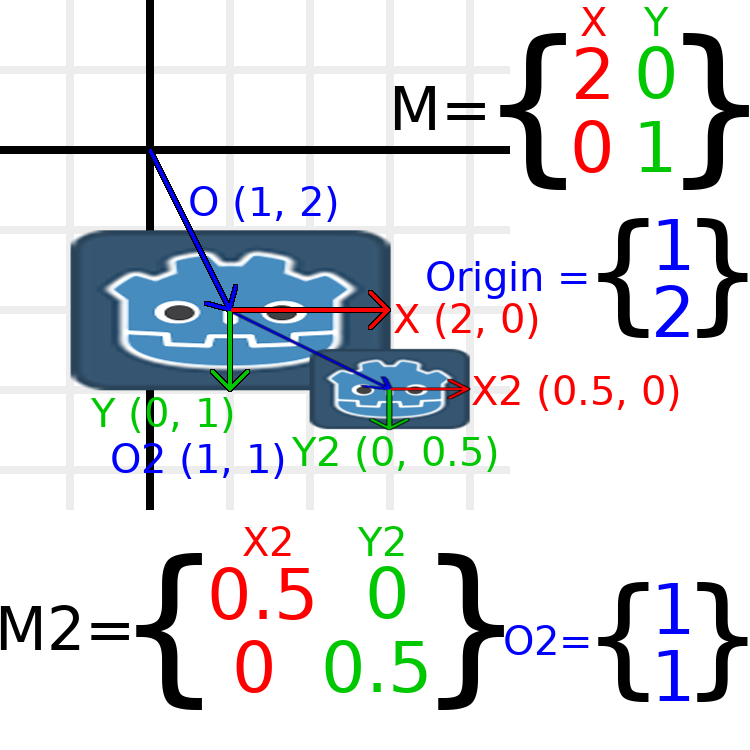
此处进行的唯一转换是父节点的比例为（2，1），子节点的比例为（0.5，0.5），两个节点的位置都被赋予了位置。

所有子转换都受父转换影响。子项的比例为（0.5，0.5），因此您希望它是一个1：1比例的正方形，并且它是（但仅相对于父项）。子项的X向量最终在世界空间中为（1、0），因为它由父项的基础向量缩放。同样，子节点的原点向量设置为（1，1），但是由于父节点的基础向量，实际上将其在世界空间中移动了（2，1）。

要手动计算子变换的世界空间变换，这是我们将使用的代码：

// 设置变换就像在图像中一样，除了使位置大 100 倍。
Transform2D parent = new Transform2D(2, 0, 0, 1, 100, 200);
Transform2D child = new Transform2D(0.5f, 0, 0, 0.5f, 100, 100);

//计算孩子的世界空间变换原点 = (2, 0) * 100 + (0, 1) * 100 + (100, 200)
Vector2 origin = parent.x * child.origin.x + parent.y * child.origin.y + parent.origin;
// basisX = (2, 0) * 0.5 + (0, 1) * 0 = (0.5, 0)
Vector2 basisX = parent.x * child.x.x + parent.y * child.x.y;
// basisY = (2, 0) * 0 + (0, 1) * 0.5 = (0.5, 0)
Vector2 basisY = parent.x * child.y.x + parent.y * child.y.y;

//将节点的变换更改为我们刚刚计算的值。
Transform = new Transform2D(basisX, basisY, origin);

在实际的项目中，我们可以使用*运算符将一个变换应用于另一个变换，从而找到孩子的世界变换：

// 设置变换就像在图像中一样，除了使位置大 100 倍。
Transform2D parent = new Transform2D(2, 0, 0, 1, 100, 200);
Transform2D child = new Transform2D(0.5f, 0, 0, 0.5f, 100, 100);

// 将节点的变换更改为孩子的世界变换。
Transform = parent * child;

==注意==

当矩阵相乘时，顺序很重要！不要把它们混在一起。

最后，应用身份转换将始终无济于事。

倒置转换矩阵

“ affine_inverse”函数返回一个“撤消”先前转换的转换。在某些情况下这可能很有用，但是仅提供一些示例会更容易。

将逆变换与法向变换相乘会撤消所有变换：

Transform2D ti = Transform.AffineInverse();
Transform2D t = ti * Transform;
// 变换是恒等变换。

通过变换及其逆变换来变换位置会导致相同位置（与“ xform_inv”相同）：

Transform2D ti = Transform.AffineInverse();
Position = Transform.Xform(Position);
Position = ti.Xform(Position);
//位置和以前一样。

这一切在3D中如何运作？

转换矩阵的一大优点是它们在2D和3D转换之间的工作原理非常相似。上面用于2D的所有代码和公式在3D中的工作方式相同，但有3个例外：添加了第三个轴，每个轴均为Vector3类型，并且Godot将基准与Transform分开存储，因为数学可以变得复杂，将其分开是有意义的。

与2D相比，有关3D中平移，旋转，缩放和剪切工作方式的所有概念都相同。要缩放，我们将每个分量乘以；要旋转，我们更改每个基本向量所指向的位置；翻译，我们操纵原点；为了剪切，我们将基本向量更改为非垂直。

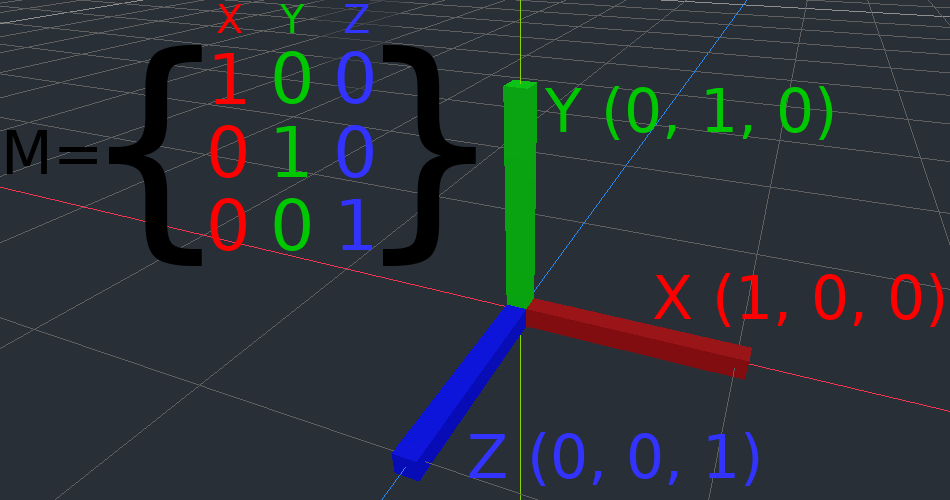
如果您愿意，最好尝试一下变换以了解它们的工作原理。Godot允许您直接从检查器编辑3D变换矩阵。您可以下载带有彩色线条和立方体的项目，以帮助可视化2D和3D中的 基础向量和原点：https://github.com/godotengine/godot-demo-projects/tree/master/misc/matrix_transform

==注意==

Godot
3.2的检查器中Spatial的“矩阵”部分将矩阵换位显示，列为水平，行为垂直。在将来的Godot版本中，可以对此进行更改以减少混乱。

==注意==

您不能直接在Godot 3.2的检查器中编辑Node2D的变换矩阵。这可能会在Godot的将来版本中更改。

表示3D旋转（高级）

2D和3D转换矩阵之间的最大区别在于，如何在没有基向量的情况下自己表示旋转。

使用2D，我们有一个简单的方法（atan2）在转换矩阵和角度之间切换。在3D中，我们不能简单地将旋转表示为一个数字。有一种称为欧拉角的东西，可以将旋转表示为一组3个数字，但是，它们是有限的，除了琐碎的情况外，它不是很有用。

在3D中，我们通常不使用角度，或者使用变换基础（在Godot中几乎所有地方都使用过），或者使用四元数。Godot可以使用Quat结构表示四元数。我建议您完全忽略它们在后台的工作方式，因为它们非常复杂且不直观。