【愚公系列】2021年11月 C#版 数据结构与算法解析(Trie树)

/// <summary>
/// trie中的键通常是字符串，但也可以是其它的结构。trie的算法可以很容易地修改为处理其它结构的有序序列，比如一串数字或者形状的排列。比如，bitwise trie中的键是一串比特，可以用于表示整数或者内存地址。
///使用Trie往往是为了实现单词查找或者统计频率.
/// </summary>
public class TNode
{
    public Dictionary<char, TNode> Childs { get; set; }
    public bool EndOfWrod { get; set; }
}

public class Trie
{
    private TNode _root = new TNode();

    public void Add(string word)
    {
        var currentNode = _root;
        for (int i = 0; i < word.Length; i++)
        {
            if (!currentNode.Childs.ContainsKey(word[i]))
            {
                currentNode.Childs.Add(word[i], new TNode());
            }
            currentNode = currentNode.Childs[word[i]];
        }
        currentNode.EndOfWrod = true;
    }

    public bool Contains(string word)
    {
        return GetLastNode(word).EndOfWrod;
    }

    public bool StartWith(string preFix)
    {
        return GetLastNode(preFix) != null;
    }

    private TNode GetLastNode(string word)
    {
        var currentNode = _root;
        for (int i = 0; i < word.Length; i++)
        {
            if (!currentNode.Childs.ContainsKey(word[i]))
            {
                return null;
            }
            currentNode = currentNode.Childs[word[i]];
        }
        return currentNode;
    }
}

Trie树又叫“字典树”，是一种在字符串计算中极为常见的数据结构。在介绍Trie树的具体结构之前，我们首先要搞明白的就是Trie树究竟是用来解决哪一类问题的，为什么这类问题可以用Trie树高效的解决。

我们为什么用Trie树

1. 节约字符串的存储空间

假设现在我们需要对海量字符串构建字典。所谓字典就是一个集合，这个集合包含了所有不重复的字符串，字典在对文本数据做信息检索系统时的作用我想毋庸赘述了。那么现在就出现了一个问题，那就是字典对存储空间的消耗过大。而当这些字符串中存在大量的串拥有重复的前缀时，这种消耗就显得过于浪费了。比如:“ababc”,“ababd”,“ababrf”,“abab…”,…，这些字符串几乎都拥有公共前缀”abab”。 我们直接的想法是，能不能通过一种存储结构节约存储成本，使得所有拥有重复前缀的串对于公共前缀只存储一遍。这种存储的应用场景如果是对DNA序列的存储，那么出现重复前缀的可能性更大，空间需求也就更为强烈。

2. 字符串检索

检索一个字符串是否属于某个词典时，我们当前一般有两种思路：

线性遍历词典，计算复杂度O(n)，n为词典长度；
利用hash表，预先处理字符串集合。这样再搜索运算时，计算复杂度O(1)。但是hash计算可能存在碰撞问题，一般的解决办法比如对某个hash值所代表的字符串实施二次检索，则计算时间也会上来。而且，hash虽说是一种高效算法，其计算效率比直接字符匹配还是要略高的。
所以，能不能设计一种高效的数据结构帮助解决字符串检索的问题？

3. 字符串公共前缀问题

这里有两个非常典型的例子：

求取已知的n个字符串的最长公共前缀，朴素方法的时间复杂度为O(nt)，t为最长公共前缀的长度；
给定字符串a，求取a在某n个字符串中和哪些串拥有公共前缀
对于问题(2)，除了朴素的比较法之外，我们还可以采取对每个字符串的所有前缀计算hash值的方法，这样一来，计算所有前缀hash值复杂度O(n∗len)，len为字符串的平均长度，查询的复杂度为O(n)。虽然降低了查询复杂度，但是计算hash值显然费时费力。

Trie树的构造

1. 结构

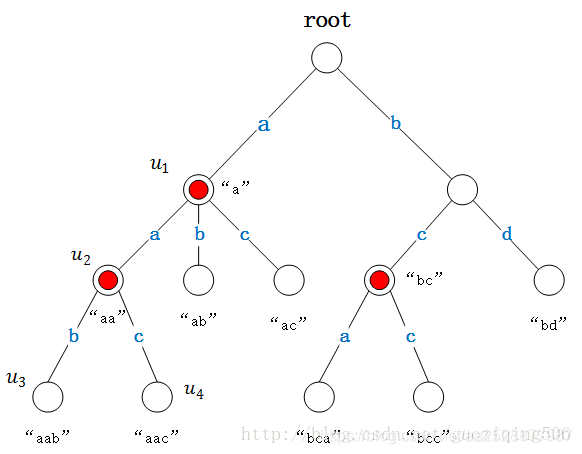
Trie树是如图所示的一棵多叉树。其中存储的字符串集合为:
{“a”,“aa”,“ab”,“ac”,“aab”,“aac”,“bc”,“bd”,“bca”,“bcc”}