【数据结构和算法】13张图解+实例+实战题目,二叉树存储结构详解
🎈 作者:Linux猿
🎈 简介:CSDN博客专家🏆,华为云享专家🏆,Linux、C/C++、面试、刷题、算法尽管咨询我,关注我,有问题私聊!
🎈 欢迎小伙伴们点赞👍、收藏⭐、留言💬
🎈 作者:Linux猿
🎈 简介:CSDN博客专家🏆,华为云享专家🏆,数据结构和算法、C/C++、面试、刷题、Linux尽管咨询我,关注我,有问题私聊!
🎈 欢迎小伙伴们点赞👍、收藏⭐、留言💬
学习二叉树之前,首先要知道二叉树如何存储,有哪些存储结构。本文就来讲解下二叉树的存储结构。
🍓一、顺序存储结构
✨1.1 存储方式
顺序存储通常与链式存储相对应,顺序存储指将二叉树结点存储到一段连续的存储空间内。
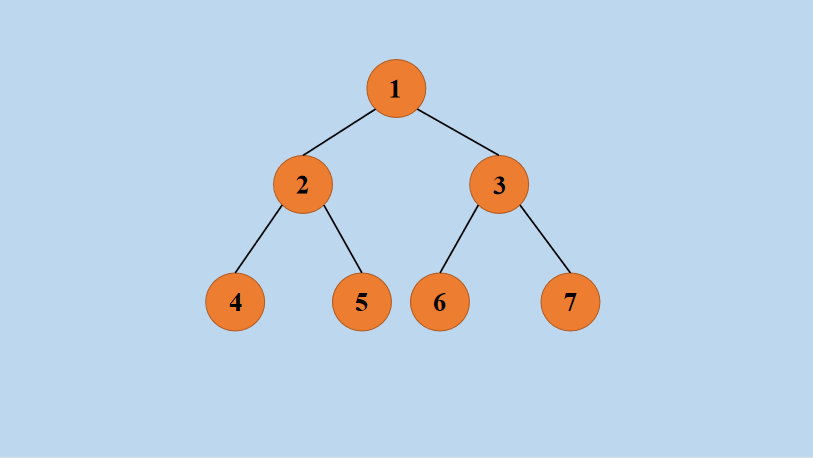
下面直接来看一个简单的例子,假设有如下二叉树:
在上图中,是一个具有 7 个结点的满二叉树,使用如下存储结构:
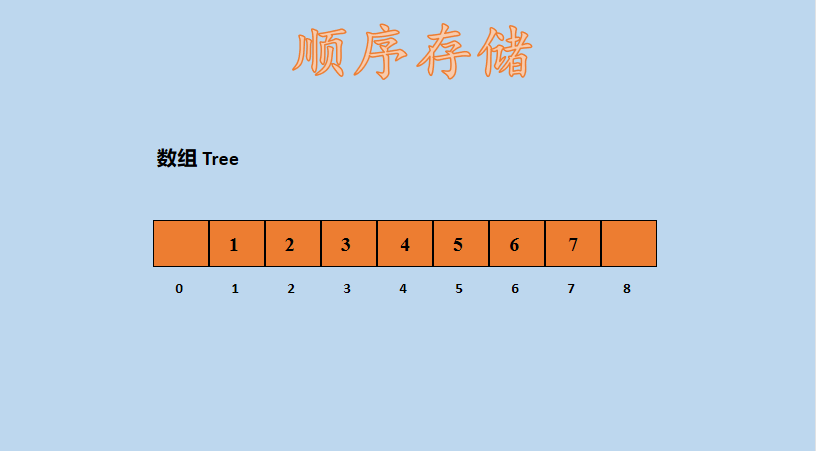
存储到数组 Tree 中后,数组中存储的值为:
在上图中,数组 Tree 中存储了二叉树结点的值,注意:这里是从下表 1 开始存储的,因为这样计算结点之间的关系更好计算,假设某一结点的下标为 i,则结点之间的关系为:
✨1.2 优缺点
🚩1.2.1 优点
使用顺序结构存储二叉树不用频繁分配空间,能够通过下标很方便的访问当前结点的左右孩子节点或者是父节点,直接通过下标来计算,看一下公式:
🚩1.2.2 缺点
从上面看,使用数组存储二叉树是很方便的,通过下标就可以直接访问对应结点的值,那么问题就来了,顺序存储结构可能会浪费存储空间,在最开始的例子中,我们是拿满二叉树(也是一棵完全二叉树)来举例的,这种情况下空间不会浪费。
那么,来看下面这种情况:
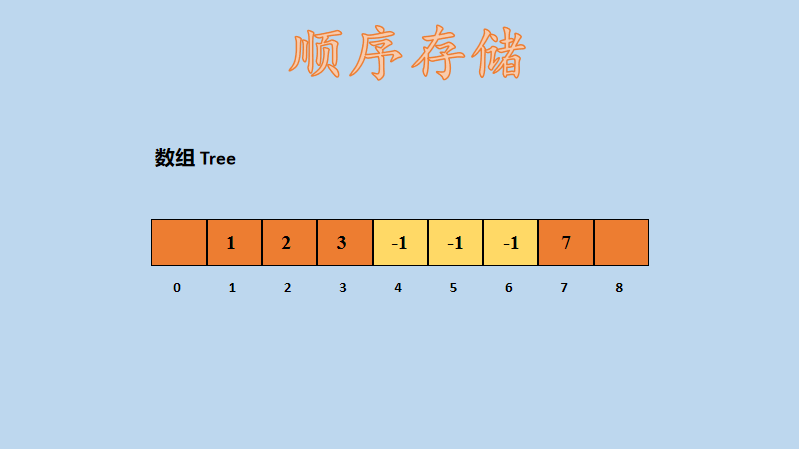
假设是上面一棵二叉树,同样是用数组进行存储,那么,存储形式如下所示:
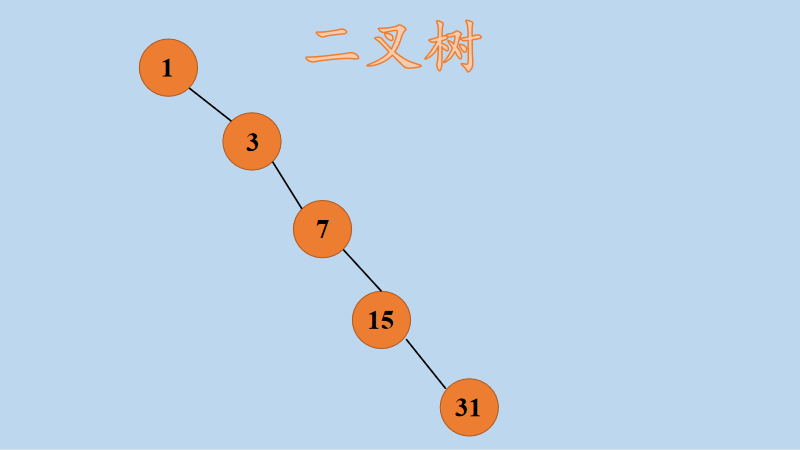
在上图中,-1 表示该结点为空(图中淡黄色部分),很明显,使用顺序存储结构后,有三个数组元素是空的,假设是一棵更大的单支二叉树,比如下面这种:
上图这种形式的二叉树就会浪费更多的空间。
🔶🔶🔶🔶🔶 我是华丽的分割线 🔶🔶🔶🔶🔶
🍓二、链式存储结构
链式存储结构能够大大节约存储空间。二叉树的链式存储结构一般有两种方法,分别是:左右孩子法和孩子兄弟法。
✨2.1 二叉链表—左右孩子法
左右孩子法是一种常见的二叉链表存储方式,即:每个结点有两个指针,左指针和右指针,分别指向左孩子和右孩子,如下所示:
单个结点的存储结构通常是如下形式:
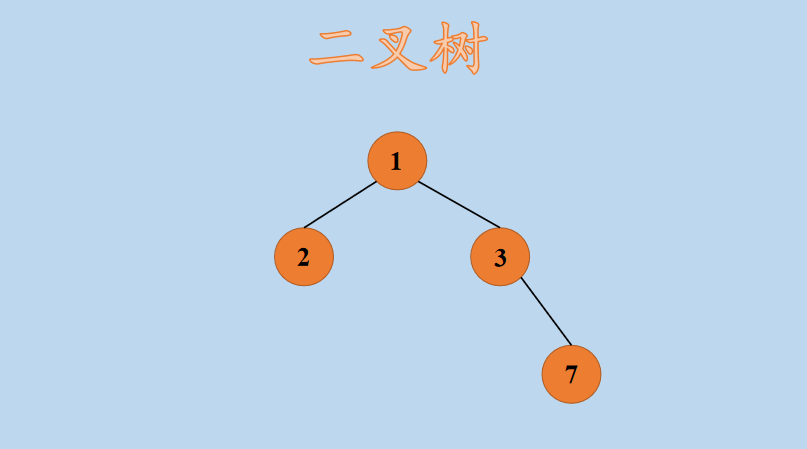
假设有如下形式的二叉树,如下所示:
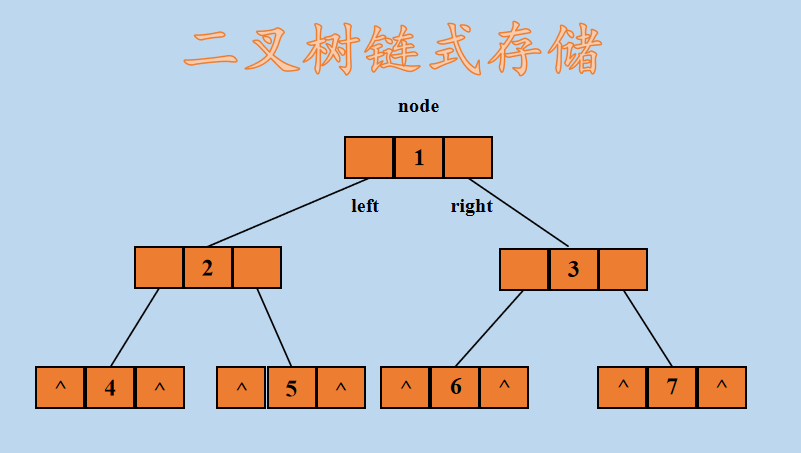
那么,使用二叉链表左右孩子法存储后,如下所示:
如果要访问结点 7,假设当前结点为 node,node->right->right 即为节点 7。
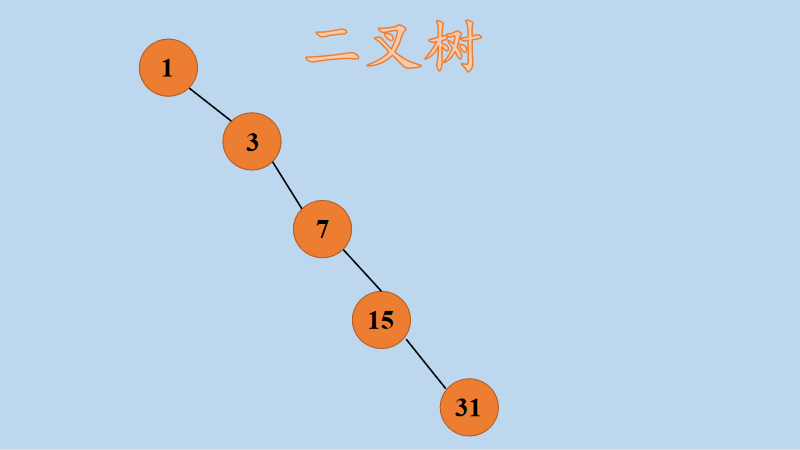
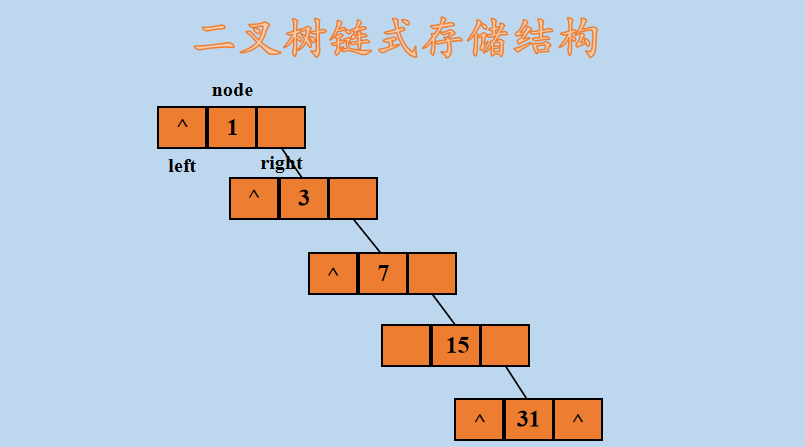
下面再来看一下比较稀疏的二叉树,二叉树如下所示:
那么,使用二叉链表左孩子右兄弟存储后,如下所示:
可以看到,与顺序存储结构相比,链式存储结构节约了很多的空间。
✨2.2 二叉链表—孩子兄弟法
二叉链表的孩子兄弟法是指结点的左指针指向第一个孩子(二叉树即为左孩子),右指针指向当前结点的下一个兄弟结点,如下所示:
单个结点的存储结构通常是如下形式:
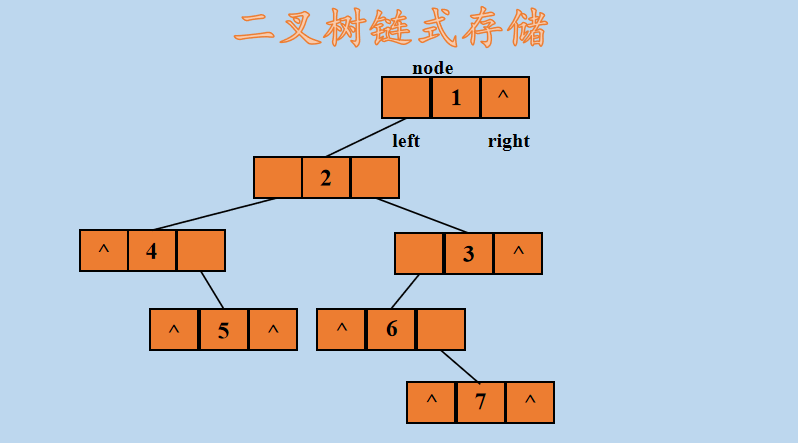
假设有如下形式的二叉树,如下所示:
那么,使用二叉链表孩子兄弟法存储后,如下所示:
✨2.3 三叉链表
三叉链表是指比二叉链表左右孩子法多了一个指针,该指针指向其父节点。如下所示:
单个结点的存储结构通常是如下形式:
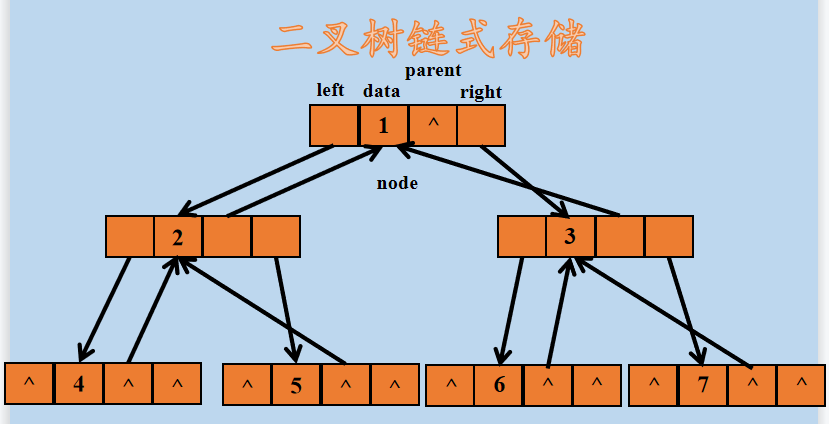
假设有如下形式的二叉树,如下所示:
那么,使用二叉链表孩子兄弟法存储后,如下所示:
在上图中,每个结点都多了一个指向父结点的指针,根结点(图中值为 1 的结点)指向父结点的指针为空,因为根结点没有父节点。
🔶🔶🔶🔶🔶 我是华丽的分割线 🔶🔶🔶🔶🔶
🍓三、LeetCode 二叉树题目
下面列出了 LeetCode 相关题目,赶紧来练习下吧!
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
🔶🔶🔶🔶🔶 我是华丽的分割线 🔶🔶🔶🔶🔶
🍓四、总结
LeetCode 对应题目的题解会更新在文章底部的公众号中,记得关注哦!
二叉链表的存储方式重点掌握二叉链表的左右孩子法和孩子兄弟法,其次要掌握三叉链表存储,最后记得做题巩固!
- 点赞
- 收藏
- 关注作者


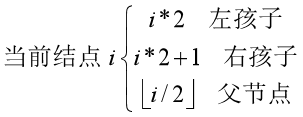



评论(0)