一看就懂 ! 图解归并排序
大家好,我是bigsai,我们今天来谈谈归并排序算法。
归并排序(Merge Sort)是建立在归并操作上的一种有效,稳定的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
一、算法思想
归并排序的主要思想是分治法。主要过程是:
1. 将n个元素从中间切开,分成两部分。
2. 将剩下的数组通过递归的方式一直分割,直到数组的大小为 1,此时只有一个元素,那么该数组就是有序的了。
3. 从最底层开始逐步合并两个排好序的数列。把两个数组大小为1的合并成一个大小为2的有序数列,再把两个大小为2有序数列的合并成4的有序数列 … 直到全部小的数组合并起来。
二、思考
那么如何将两个有序数列合成一个有序的数列呢?
我们举个栗子把,一看就懂啦

 。
。
三、举个栗子
例如有数组 arr [3,7,8,10,2,4,6,9]; 我们可以把这个数组分成两个有序的子序列。
分别为 [3, 7, 8, 10] 和 [2, 4, 6, 9],并将其合并为有序序列[2,3,4,6,7,8,9,10]。
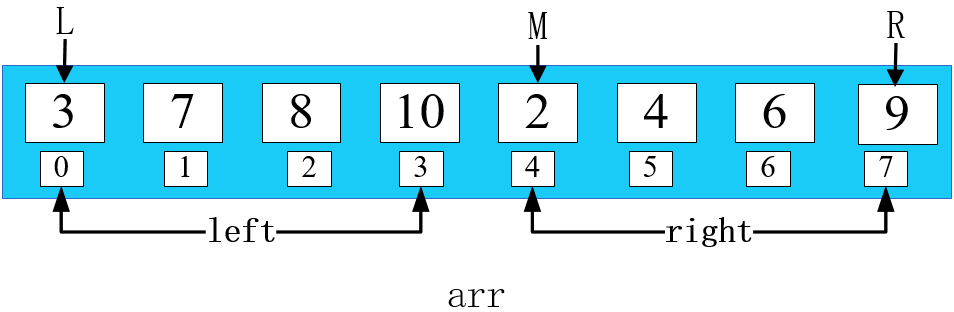
第一步:
把这两个小的数组拆分为 left 数组和 right 数组。如下图所示,使用 i 指向 left 的第一个元素, 使用 j 指向 right 的第一个元素。
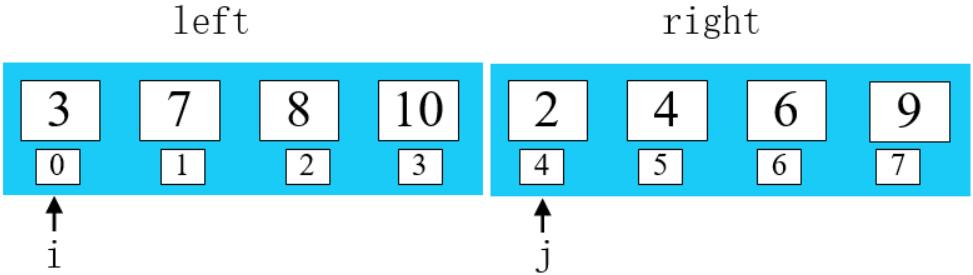
第二步:
建立一个空数组 arr ,使用 k 指向数组第一个元素。
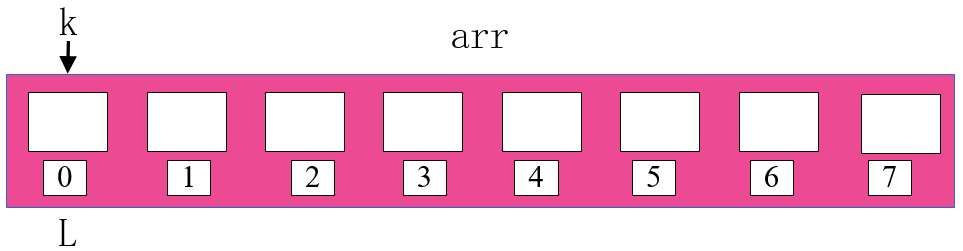
第三步:
比较 i 和 j 所指数字,将小的数字放在 k 所指位置。同时将小的数字所指位置和 k 所指位置向右移一位。
2 < 3 , 将 2 填入 arr 数组 ,同时右移 j 和 k。
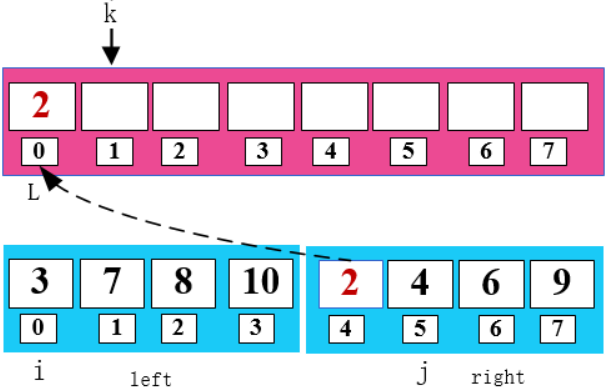
3 < 4 , 将 3 填入 arr 数组 ,同时右移 i 和 k。
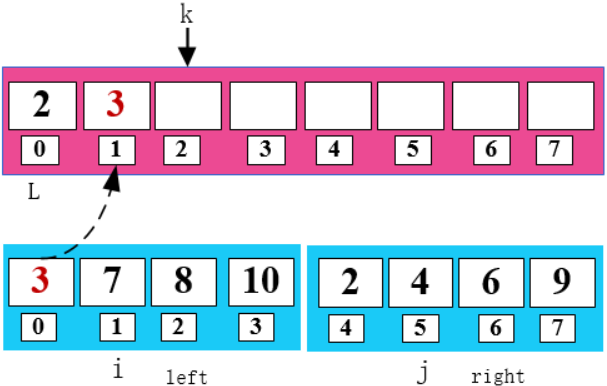
4 < 7,将 4 填入 arr 数组,同时右移 j 和 k。
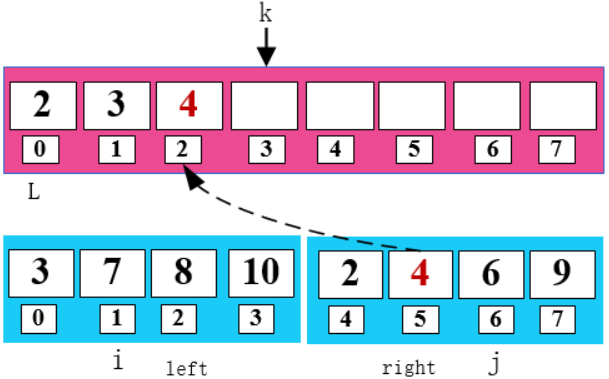
6 < 7,将 6 填入 arr 数组,同时右移 j 和 k。
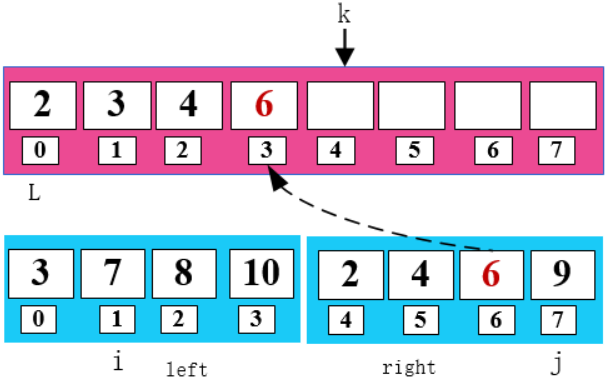
7 < 9,将 7 填入 arr 数组,同时右移 i 和 k。
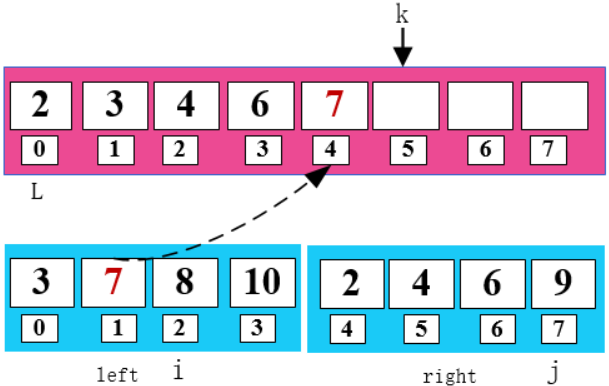
8 < 9,将 8 填入 arr 数组,同时右移 i 和 k。
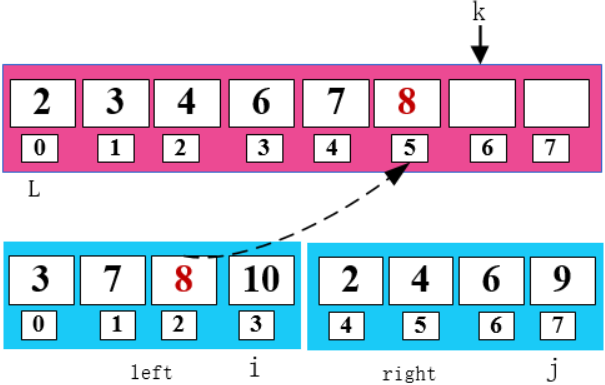
10 > 9,将 9 填入 arr 数组,同时右移 j 和 k。
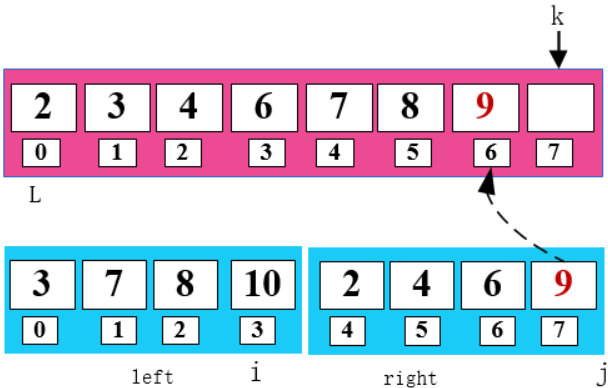
可以发现此时 right 数组已经填完了,所以此时只需要把 left 数组剩下的数字填入 arr 即可。
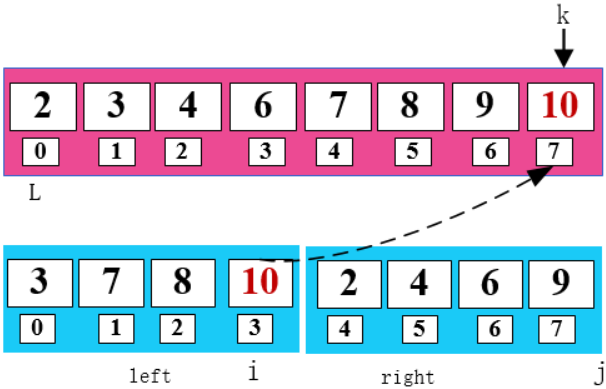
一顿操作猛如虎,这样就把两个有序的数组通过归并的方式排好顺序啦,是不是很赞。
那么问题来了,难道归并排序只能排这种有序的数组么?
那出现一个无序的数组该咋办呢?例如这个数组现在变为 arr [8,7,2,10,3,9,4,6];
四、问题解决
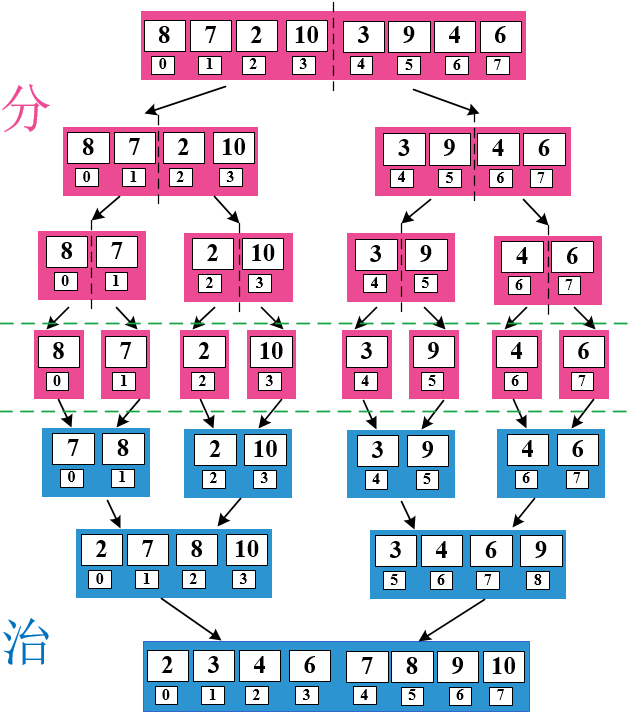
此刻需要运用分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
其实上面第三部分就是治(conquer)的过程,将两个有序的序列合成为一个有序的序列。
小栗子:图解无序序列进行希尔排序。
五、算法实现
-
#include <stdio.h>
-
-
void merge(int arr[], int L, int M, int R) {
-
int LEFT_SIZE = M - L;
-
int RIGHT_SIZE = R - M + 1;
-
int left[LEFT_SIZE];
-
int right[RIGHT_SIZE];
-
int i, j, k;
-
-
// 填充左边的数组
-
for (i=L; i<M; i++){
-
left[i-L] = arr[i];
-
}
-
-
// 填充右边的数组
-
for (i=M; i<=R; i++){
-
right[i-M] = arr[i];
-
}
-
-
// for (int i=0; i<LEFT_SIZE; i++){
-
// printf("%d\n",left[i]);
-
// }
-
//
-
// for (int i=0; i<RIGHT_SIZE; i++){
-
// printf("%d\n",right[i]);
-
// }
-
-
// 合并数组
-
i = 0; j = 0; k = L;
-
while (i < LEFT_SIZE && j < RIGHT_SIZE){
-
if (left[i] < right[j]){
-
arr[k] = left[i];
-
i++;
-
k++;
-
}else{
-
arr[k] = right[j];
-
j++;
-
k++;
-
}
-
}
-
-
while(i < LEFT_SIZE){
-
arr[k] = left[i];
-
i++;
-
k++;
-
}
-
while(j < RIGHT_SIZE){
-
arr[k] = right[j];
-
j++;
-
k++;
-
}
-
-
}
-
-
void mergeSort(int arr[], int L, int R){
-
if (L == R){
-
return;
-
}else{
-
int M = (L + R) / 2;
-
mergeSort(arr,L,M);
-
mergeSort(arr, M+1,R);
-
merge(arr, L, M+1,R);
-
}
-
}
-
-
int main(){
-
// int arr[] = {3,7,8,10,2,4,6,9};
-
int arr[] = {8,7,2,10,3,9,4,6};
-
int L = 0;
-
int M = 4;
-
int R = 7;
-
mergeSort(arr,L,R);
-
-
for (int i=0; i<=R; i++){
-
printf("%d\n",arr[i]);
-
}
-
}
输出:
六、算法分析
时间复杂度:O(nlogn)。
空间复杂度:O(N),归并排序需要一个与原数组相同长度的数组做辅助来排序。
稳定性:稳定,因为交换元素时,可以在相等的情况下做出不移动的限制,所以归并排序是可以稳定的。
七、适用场景
归并排序需要一个跟待排序数组同等空间的临时数组,因此,使用归并排序时需要考虑是否有空间上的限制。如果没有空间上的限制,归并排序是一个不错的选择。

关注下方公众号,分享硬核知识
文章来源: bigsai.blog.csdn.net,作者:Bigsai.,版权归原作者所有,如需转载,请联系作者。
原文链接:bigsai.blog.csdn.net/article/details/121413503
- 点赞
- 收藏
- 关注作者

评论(0)