R语言实战案例-蒙特卡罗方法（附实现代码）

前言

蒙特卡罗模拟已成为衍生证券定价和风险管理的重要工具，这些应用反过来刺激了对新的蒙特卡罗方法的研究，并重新引起了人们对某些旧有技术的兴趣。

Monte Carlo simulation has become an essential tool in the pricing of derivative securities and in risk management. These applications have, in turn, stimulated research into new Monte Carlo methods and renewed interest in some older techniques.

除此之外，蒙特卡罗模拟在宏观经济学、生物医学、计算物理学等众多领域应用广泛。

蒙特卡罗方法的思路可以追溯到蒲丰投针试验：

1777年，蒲丰伯爵乔治·路易斯·勒克莱尔（Georges-Louis Leclerc De Buffon，1707-1788）进行了投针试验：设平面上画有等距为a的一簇平行线，取一枚长度小于a的针随意扔到平面上，通过计算针与平行线相交的概率，可以得到圆周率π的估计值（2ln）/（ak），其中l为针的长度，n为随机投针的次数，k为针与线相交的次数。

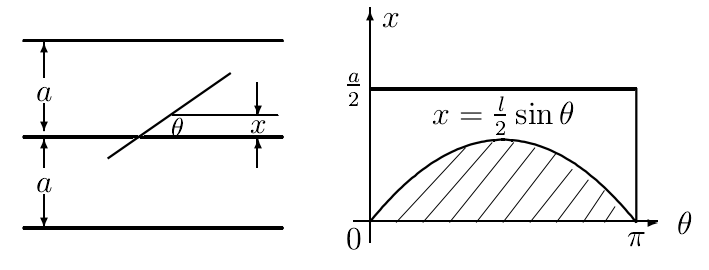
图：蒲丰投针的几何概率计

文章来源: wenyusuran.blog.csdn.net，作者：文宇肃然，版权归原作者所有，如需转载，请联系作者。

原文链接：wenyusuran.blog.csdn.net/article/details/120758491