Monge矩阵(算法导论)
Monge矩阵
对一个m*n的实数矩阵A,如果对所有i,j,k和l,1≤ i<k ≤ m和1≤ j<l ≤ n,有 A[i,j]+A[k,l] ≤ A[i,l]+A[k,j] 那么,此矩阵A为Monge矩阵。
换句话说,每当我们从矩阵中挑出两行与两列,并且考虑行列交叉处的4个元素,左上角与右下角的和小于或等于左下角与右上角元素的和。
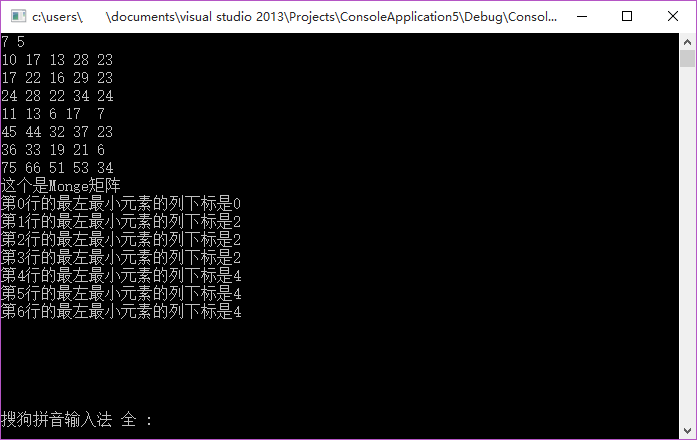
例如,下面这个就是一个Monge矩阵

(1)证明一个矩阵为Monge阵,当且仅当对所有i=1,2,...,m-1和j=1,2,...,n-1,有 A[i,j]+A[i+1,j+1] ≤ A[i,j+1]+A[i+1,j]
(提示:在当部分,对行、列分别使用归纳法。)

(2)下面的矩阵不是Monge阵。改变一个元素,把它变成Monge矩阵
37 23 22 32
21 6 27 10
53 34 30 31
32 13 9 6
43 21 15 8
很明显是要改27,27可以改成【2,5】内的任何一个实数
(3)假设f(i)是第i行包含最左端最小值的列的索引值。证明对任何的m x n Monge矩阵,有f(1) ≤ f(2) ≤...≤ f(m)。

(4)下面是一个用来计算m x n 的Monge矩阵A中每一行的最左最小值的分治算法的描述:
构造一个包含所有A的偶数行的子矩阵A'。递归地计算A'中每一行的最左端最小值。然后计算A中奇数行的最左端最小值。
解释如何能在O(m+n)时间内计算出A的奇数行的最左端最小值?(在偶数行最左最小值已知的情况下)
解释:看下面的代码就很明显了。
其实这个算法,我个人感觉,就结构而言比较像分治,但是就思想而言比较像动态规划。
(5)写出(4)所描述算法的运行时间的递归式,并证明其解为O(m+nlogm)
T(m)=T(m/2)+ O(m+n)(求解略)
我的代码:
-
#include<iostream>
-
using namespace std;
-
-
void calculate(double **A, int r1, int r2, int min, int max, int *f) //计算f(r1)到f(r2)
-
{
-
if (r1 > r2)return;
-
int r = (r1 + r2) / 2;
-
int result = min;
-
int flag = A[r][min];
-
for (int i = min + 1; i <= max; i++) //寻找最左最小元素flag,和它的的下标result
-
{
-
if (A[r][i] < flag)
-
{
-
flag = A[r][i];
-
result = i;
-
}
-
}
-
f[r] = result;
-
calculate(A, r1, r - 1, min, result, f);
-
calculate(A, r + 1, r2, result, max, f);
-
}
-
-
bool isMonge(double **A, int m, int n) //判断是否是Monge矩阵
-
{
-
for (int i = 0; i < m - 1; i++)for (int j = 0; j < n - 1; j++)if (A[i][j] + A[i + 1][j + 1]>A[i + 1][j] + A[i][j + 1])return false;
-
return true;
-
}
-
int main()
-
{
-
int m, n;
-
while (cin >> m >> n && m>1 && n > 1)
-
{
-
double **A = new double*[m]; //Monge矩阵
-
int *f = new int[m]; //不需要在主函数里面进行初始化,这个工作由calculate函数完成
-
for (int i = 0; i < m; i++)
-
{
-
A[i] = new double[n];
-
for (int j = 0; j < n; j++)cin >> A[i][j];
-
}
-
if (isMonge(A, m, n))
-
{
-
cout << "这个是Monge矩阵" << endl;
-
calculate(A, 0, m - 1, 0, n - 1, f);
-
for (int i = 0; i < m; i++)cout << "第" << i << "行的最左最小元素的列下标是" << f[i] << endl;
-
}
-
else cout << "这个不是Monge矩阵";
-
}
-
return 0;
-
}
-
文章来源: blog.csdn.net,作者:csuzhucong,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/nameofcsdn/article/details/52076228
- 点赞
- 收藏
- 关注作者


评论(0)