外固——求马的外固数和外固集

智力游戏

61象棋（5）

优秀书籍

对于8*8的棋盘，求马的外固数和外固集

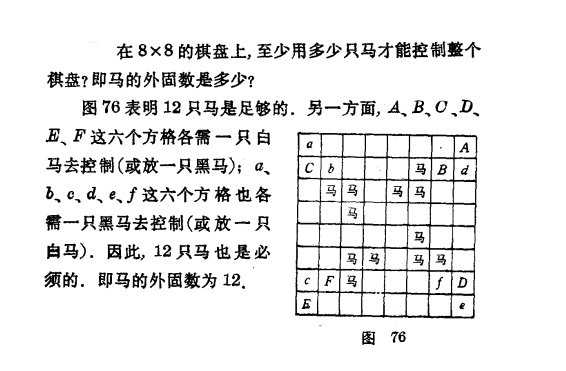
所以外固数自然是12了，那么外固集有哪些呢？

我的解法：（下面所有的内容都是自己想的，后来才看到书上这一页）

初始代码是用24层的循环进行找答案试试，虽然要运行结束不太现实，但是如果运气好，循环只进行了很少一部分，就得到了答案，也不是不可能

#include<iostream>
using namespace std;

void exist(int list[][8], int i, int j)		//将可以到达的8个（或少于8个）格子记录下“已经覆盖”
{
	if (i > -1 && i<8 && j>-1 && j < 8)list[i][j] = 1;
}

void place_a_horse(int list[][8], int i, int j)		//更新已经覆盖的格子的信息
{
	list[i][j] = 1;
	exist(list, i - 2, j - 1);
	exist(list, i - 2, j + 1);
	exist(list, i - 1, j - 2);
	exist(list, i - 1, j + 2);
	exist(list, i + 2, j + 1);
	exist(list, i + 2, j - 1);
	exist(list, i + 1, j + 2);
	exist(list, i + 1, j - 2);
}

void action(int list[][8], int i1, int j1, int i2, int j2, int i3, int j3, int i4, int j4, int i5, int j5, int i6, int j6, int i7, int j7, int i8, int j8, int i9, int j9, int ia, int ja, int ib, int jb, int ic, int jc)
{
	for (int i = 0; i < 8; i++)for (int j = 0; j < 8; j++)list[i][j] = 0;
	place_a_horse(list, i1, j1);		//放入12个棋子
	place_a_horse(list, i2, j2);
	place_a_horse(list, i3, j3);
	place_a_horse(list, i4, j4);
	place_a_horse(list, i5, j5);
	place_a_horse(list, i6, j6);
	place_a_horse(list, i7, j7);
	place_a_horse(list, i8, j8);
	place_a_horse(list, i9, j9);
	place_a_horse(list, ia, ja);
	place_a_horse(list, ib, jb);
	place_a_horse(list, ic, jc);

for (int i = 0; i < 8; i++)for (int j = 0; j < 8; j++)if (list[i][j] == 0)return;
cout << i1 << j1 << i2 << j2 << i3 << j3 << "  " << i4 << j4 << i5 << j5 << i6 << j6 << "  ";
cout << i7 << j7 << i8 << j8 << i9 << j9 << "  " << ia << ja << ib << jb << ic << jc << endl;
cout << list[2][0] << endl;
}

//12个棋子从上往下遍历循环
void visit12(int list[][8])
{
	for (int i1 =  0; i1 < 3; i1++) for (int j1 = 0; j1 < 8; j1++)
	for (int i2 = i1; i2 < 3; i2++)	for (int j2 = 0; j2 < 8; j2++)
	for (int i3 = i2; i3 < 3; i3++)	for (int j3 = 0; j3 < 8; j3++)
	for (int i4 = i3; i4 < 3; i4++)	for (int j4 = 0; j4 < 8; j4++)

	for (int i5 = i4; i5 < 8; i5++)	for (int j5 = 0; j5 < 8; j5++)
	for (int i6 = i5; i6 < 8; i6++)	for (int j6 = 0; j6 < 8; j6++)
	for (int i7 = i6; i7 < 8; i7++)	for (int j7 = 0; j7 < 8; j7++)
	for (int i8 = i7; i8 < 8; i8++)	for (int j8 = 0; j8 < 8; j8++)

	for (int i9 =  5; i9 < 8; i9++) for (int j9 = 0; j9 < 8; j9++)
	for (int ia =  5; ia < 8; ia++) for (int ja = 0; ja < 8; ja++)
	for (int ib =  5; ib < 8; ib++) for (int jb = 0; jb < 8; jb++)
	for (int ic =  5; ic < 8; ic++) for (int jc = 0; jc < 8; jc++)
		action(list, i1, j1, i2, j2, i3, j3, i4, j4, i5, j5, i6, j6, i7, j7, i8, j8, i9, j9, ia, ja, ib, jb, ic, jc);
}


int main()
{
	int list[8][8];
	visit12(list);
	cout << "end";
	system("pause>nul");
	return 0;
}

结果运气并不好，得不到答案。

于是我决定尝试先找找有没有非常规则的答案。

第一种，上下对称且左右对称

void visit3(int list[][8])		//只对左上角的3个进行遍历循环
{
	for (int i1 =  0; i1 < 3; i1++)	for (int j1 = 0; j1 < 4; j1++)
	for (int i2 = i1; i2 < 4; i2++)	for (int j2 = 0; j2 < 4; j2++)
	for (int i3 = i2; i3 < 4; i3++)	for (int j3 = 0; j3 < 4; j3++)
	action(list, i1, j1, i2, j2, i3, j3, 7 - i1, j1, 7 - i2, j2, 7 - i3, j3, i1, 7 - j1, i2, 7 - j2, i3, 7 - j3, 7 - i1, 7 - j1, 7 - i2, 7 - j2, 7 - i3, 7 - j3);//上下对称，左右对称
}

可惜，并没有这样的答案。

第二种，上下对称的

void visit6(int list[][8])
{
	for (int i1 =  0; i1 < 3; i1++) for (int j1 = 0; j1 < 8; j1++)
	for (int i2 = i1; i2 < 3; i2++)	for (int j2 = 0; j2 < 8; j2++)
	for (int i3 = i2; i3 < 3; i3++)	for (int j3 = 0; j3 < 8; j3++)
	for (int i4 = i3; i4 < 3; i4++)	for (int j4 = 0; j4 < 8; j4++)
	for (int i5 = i4; i5 < 8; i5++)	for (int j5 = 0; j5 < 8; j5++)
	for (int i6 = i5; i6 < 8; i6++)	for (int j6 = 0; j6 < 8; j6++)
	action(list, i1, j1, i2, j2, i3, j3, i4, j4, i5, j5, i6, j6,7-i1,j1,7-i2,j2,7-i3,j3,7-i4,j4,7-i5,j5,7-i6,j6);	//上下对称
}

可惜，并没有这样的答案。

接下来就是准备尝试最后一种了，不是轴对称，而是旋转对称。

但是这时我发现，2个马无法控制左上角的2*2的正方形，为了控制左上角的4个格子，左上角的16个格子里面一定至少有3个马。恰好一共12个马，所以每个4*4的角落必定是恰好3个马。

于是我考虑左上角的4*4=16个格子里面，怎么样放置3个马才能覆盖左上角的4个格子

将visit3里面改成如下代码

for (int i1 = 0; i1 < 3; i1++)	for (int j1 = 0; j1 < 4; j1++)
	for (int i2 = i1; i2 < 4; i2++)	for (int j2 = 0; j2 < 4; j2++)
	for (int i3 = i2; i3 < 4; i3++)	for (int j3 = 0; j3 < 4; j3++)
	{
		for (int i = 0; i < 8; i++)for (int j = 0; j < 8; j++)list[i][j] = 0;
		place_a_horse(list, i1, j1);	
		place_a_horse(list, i2, j2);
		place_a_horse(list, i3, j3);
		if (list[0][0] && list[0][1] && list[1][0] && list[1][1])

			cout << i1 << j1 << i2 << j2 << i3 << j3 <<"   ";
	}

运行结果是

000322   001122   002223   002230   002232   002322   030022   031222   032122   032221   111222   112122   112221   121122   122223   122230   122232   122322   212223   212230   212232   212322   222123   222130   222132   222321   232122   232221   end

终于，这次运气还不错，一举发现了答案。

然后我根据上面的输出进行了排查，发现分4块循环对称的只有这1种方案（另外一种方案无非是翻转过来使得风车的方向反过来而已）。

至于有没有其他形式的答案就不清楚了。

文章来源: blog.csdn.net，作者：csuzhucong，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/nameofcsdn/article/details/52645182