2048格子位置判定

最近发现2048可以自定义：

只看下面的16个格子，不看上面的统计数据。

看到这么多格子，首先很明显，至少有1个是2，而且至少有1个是4

可能全部由2和4组成，也可能由2和4和8组成，等等。

总之，这样就有个问题，因为分不清楚不同的数字，所以很难玩下去。

下面考虑这个问题：

如果2、4、8、16等等，所有的格子都是一模一样的，那么2048会有多少种看起来不一样的局面？

根据时间，可以分为3类。

第一类：刚开始的时候，有2个格子。

第二类：某次滑动之后，系统暂时还没添加2

第三类：系统添加2之后，玩家还没滑动

这只是根据时间来分而已，它们所包含的局面互相都各有重合的，所以考虑重合的问题是本文的关键。

虽然第一类比较简单，但是第二类更规则，应该从第二类开始分析。

第二类满足一个重要的规则：所有的格子都靠着某条边。

比如说，如果最后一次滑动是向下滑，那么所有的格子都是靠着下面的。

这样，每一列都有5种情况，即这一列的格子数目是0、1、2、3、4

这样，一共是5*5*5*5=625种情况。

但是，第三类就非常复杂了。

一方面，最新添加的2的位置不好分析，另外一方面，存在既靠着下面又靠着左边的情况，这样讨论就十分复杂了。

解决这种讨论十分繁琐的问题的途径之一，自然是编程了。

首先，信息的表示。

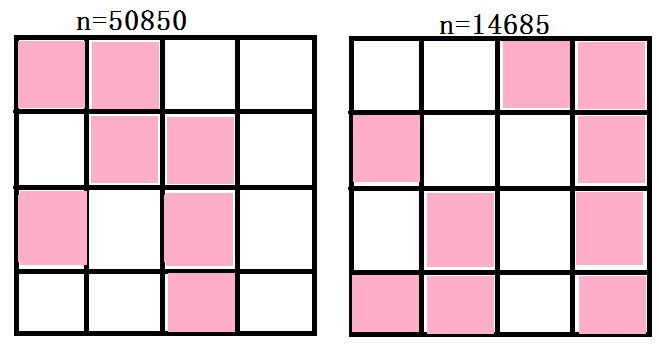
用1个16位二进制整数代表一个局面，从上到下，从左往右，比如上面的图片就是0000 0010 0011 1111

然后定义合法的局面。

合法的局面有2种，一种是刚开始的时候有2个格子，即第一类时间，

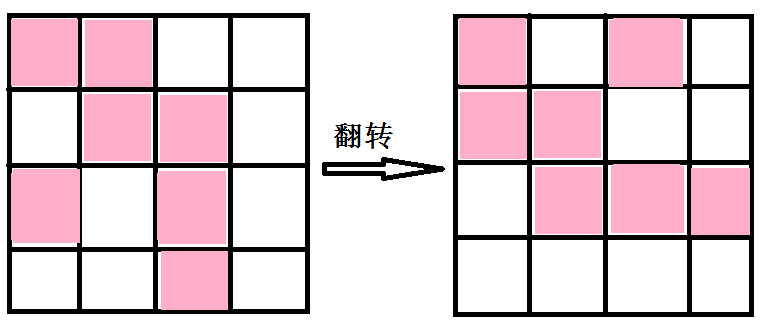
还有一种是第二类时间和第三类时间的合并，即要么全部靠着某条边，要么除了某个格子之外全部靠着某条边。

（没有格子是不算靠着边的）

除此之外的局面自然是非法的。

但是要说这些局面就一定都是合法的，还要看2048的规则。

实际上，只要是满足上述条件就一定是合法的，因为存在仅由2、4、8、16构成的对应的局面，详情略。

因为总局面只有2^16=65536种，所以直接枚举就可以了，不需要用计数的方法。

虽然4个方向是等价的，但是现在有了确定的编码方案，4个方向就不一样了，最容易判断的，是是否靠右边。

靠右边就是4行都靠右边，而一行里面，靠右边就只有5种情况：0000、0001、0011、0111、1111

判断一行的话，只需要一个简单的函数ok就行

bool ok(int n)
{
	if (n != 0 && n != 1 && n != 3 && n != 7 && n != 15)return false;
	return true;
}

bool right(int n)
{
return ok(n & 15) && ok((n >> 4) & 15) && ok((n >> 8) & 15) && ok((n >> 12) & 15);
}

bool left_or_right(int n)
{
	if (right(n))return true;
	return right(65535 - n);
}

bool all_direction(int n)
{
	if (n == 0)return false;
	if (left_or_right(n))return true;
	return left_or_right(n - (((n>>4)%2 - (n>>1)%2) * 14 + ((n>>8)%2 - (n>>2)%2) * 252 + ((n>>9)%2 - (n>>6)%2) * 448 + ((n>>12)%2 - (n>>3)%2) * 4088 + ((n>>13)%2 - (n>>7)%2) * 8064 + ((n>>14)%2 - (n>>11)%2) * 14336));
}

int main()
{	int r[65536];

	for (int i = 0; i < 65536; i++)
	{
		r[i] = 0;
		if (all_direction(i))r[i] = 1;
		for (int k = 0; k < 16; k++)if ((i&(1<<k))!=0)
		if (all_direction(i^(1<<k)))r[i] = 1;
	}
	int result = 0;
	for (int i = 0; i < 65536; i++)result += r[i];
	cout << result;
	return 0;
}

文章来源: blog.csdn.net，作者：csuzhucong，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/nameofcsdn/article/details/52961854