IQ使命2 Tikal 提卡尔(旋转的通道)攻略
目录:
本章规则:

把硬币移入洞内,如果移动到带有旋转箭头的格子,这个格子就会按照箭头的方向旋转90°
(1)

右上下右
(2)

红色的格子会全部一起旋转
左下上左上
(3)

左下右左上下右右右上左
(4)

左上下左下上右下
(5)

下左上左上左下下右下右右
(6)

上下上上下右右左右下右上左上
(7)

右上上左左下上左左下下上右
(8)

右上右下下上下下上左下左左
(9)

右上右右左右右下下左右左左下左下左上
(10)

左下右左右右左右下右
(11)

到这一关,我就编程解决了。
因为每一步移动的可选择项很少,所以直接用深度优先搜索就能得到答案
代码:
-
#include<iostream>
-
#include<stack>
-
#include<string>
-
using namespace std;
-
-
const int M = 25;//最多需要的步数
-
int l[6][6];//每个格子的旋转方向
-
bool red[6][6];//每个格子是否为红格子
-
bool con[6][6][4];//每个格子的每个方向是否有接口
-
int sr, sc, er, ec;//起点和终点的位置
-
int dr[4] = { -1, 0, 1, 0 };
-
int dc[4] = { 0, 1, 0, -1 };
-
stack<int>s, s2;
-
-
bool ok(int k)
-
{
-
int tr = sr + dr[k], tc = sc + dc[k];
-
if (tr<0 || tr>5 || tc<0 || tc>5||l[tr][tc]<0)return false;
-
return con[sr][sc][k] && con[tr][tc][(k+2)%4];
-
}
-
-
void turn(int i, int j, int times)
-
{
-
while (times--)
-
{
-
bool temp = con[i][j][3];
-
con[i][j][3] = con[i][j][2];
-
con[i][j][2] = con[i][j][1];
-
con[i][j][1] = con[i][j][0];
-
con[i][j][0] = temp;
-
}
-
}
-
-
void turn(int i, int j,bool flag)//flag=true表示正向,false表示回溯
-
{
-
if (flag)
-
{
-
if (red[i][j])
-
{
-
for (int i = 0; i < 6; i++)for (int j = 0; j < 6; j++)if (red[i][j])turn(i, j, l[i][j]);
-
}
-
else turn(i, j, l[i][j]);
-
}
-
else if (red[i][j])
-
{
-
for (int i = 0; i < 6; i++)for (int j = 0; j < 6; j++)if (red[i][j])turn(i, j, 4 - l[i][j]);
-
}
-
else turn(i, j, 4-l[i][j]);
-
}
-
-
bool trys(int deep)
-
{
-
if (deep > M)return false;
-
if (sr == er && sc == ec)return true;
-
for (int i = 0; i < 4; i++)if (ok(i))
-
{
-
sr += dr[i], sc += dc[i];
-
turn(sr, sc, true);
-
s.push(i);
-
if (trys(deep + 1))return true; //深度优先搜索
-
s.pop();
-
turn(sr, sc, false); //这里的顺序尤其哟注意
-
sr -= dr[i], sc -= dc[i];
-
}
-
return false;
-
}
-
-
int main()
-
{
-
int r, c, a;
-
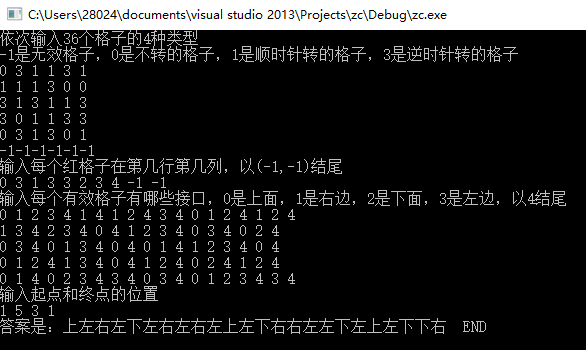
cout << "依次输入36个格子的4种类型\n-1是无效格子,0是不转的格子,1是顺时针转的格子,3是逆时针转的格子\n";
-
for (int i = 0; i < 6; i++)for (int j = 0; j < 6; j++)
-
{
-
cin >> l[i][j];
-
red[i][j] = false;
-
for (int k = 0; k < 4; k++)con[i][j][k] = false;
-
}
-
cout << "输入每个红格子在第几行第几列,以(-1,-1)结尾\n";
-
while (cin >> r >> c && r >= 0)red[r][c] = true;
-
cout << "输入每个有效格子有哪些接口,0是上面,1是右边,2是下面,3是左边,以4结尾\n";
-
for (int i = 0; i < 6; i++)for (int j = 0; j < 6; j++)
-
if(l[i][j]>=0)while (cin >> a && a != 4)con[i][j][a] = true;
-
cout << "输入起点和终点的位置\n";
-
cin >> sr >> sc >> er >> ec;
-
while (!s.empty())s.pop();
-
trys(0);
-
while (!s.empty())
-
{
-
s2.push(s.top());
-
s.pop();
-
}
-
cout << "答案是:";
-
string str[4] = { "上", "右", "下", "左" };
-
while (!s2.empty())
-
{
-
cout << str[s2.top()];
-
s2.pop();
-
}
-
cout << " END";
-
return 0;
-
}
其中M是需要的步数,通过不断调整M重新运行,还可以求出所需的最小步数
(12)

左上左左下上下下右下左右下右左右右右上左下上左
(13)

下右上右左右右下下左左左下下上下下右上右右右上右下上下下
(14)

左下上左下左上上左下下左上上下上上下上上上下右
(15)

下左左上上下上上右右右右左右右下上左右下左左右左右右上左左左右左左右左左下上右左下下下右右右下上右
这是我自己一步步尝试得到的答案,一共49步
用我的程序可以算出来,最少需要38步,38步的方案是:
下左左上上下上上右右右右左右右下左下右下下下上下左右左左左左右上左上右下上右
(16)

下下上右右下右上下右上左右上右下上下下上下下左下左左上下左右上右左上下下左左
(17)

左下右下右右左右上下左左上右
(18)

左右右左下左下下右上左左上下上上上下上上右
(19)

下右下右上下上上右右下右左左下右上上右
(20)

右下左左上右上上上右左上右左左下上左左下下下上下上上下上上左
(21)

上左上左上下右左下下上右左右右下上右右上右下下下下上左上左
(22)

左左下上上上上下上上右右左右左左下上左下上左左右左下
(23)

右左上右左左左下下上下下右右下上左右下下右右左右右上
(24)

左右左左上上左上右左左右左左上右右上左左
(25)

左下上左上下上下下上下下上右左右右下右下右左上下右左上上
(26)

下右下左右上上右左上右上上右右左右右下下
(27)

右上左右上下下左右下下上下下左左右左左左上左下上上右
(28)

右上左右上下下右上右左上
(29)

上右上左左下上左右右下上左下左下左右下下右下右上右左右右上上下上上下上上
(30)

下左右下上右左上下左下左右上下左左左右右左右右上下左右上左左下左上下上上上右
(31)

左左右左下右下下左下右上下右上右右上下右下上左下上左右上右上下下下下左左左
(32)

左上下右左上左上下下上下下右上右左下右下下左上下右右左右右右上下上上左上下左

这是一个彩蛋,其实就是猜数游戏,规则:猜数游戏

成就:

the grand champion of rotation 通关即可
the secret of 10 steps 在10步之内完成整个游戏(这到底是什么意思我也不知道,反正按照我这样完成每一关就能完成这个成就)
π of the mayan people 移动到所有固定的边界(还是不知道是什么意思,而且第6关的固定的边界明显无法达到)
文章来源: blog.csdn.net,作者:csuzhucong,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/nameofcsdn/article/details/72833992
- 点赞
- 收藏
- 关注作者


评论(0)