穿插纸条 （第73-90关）终点和连通性对于拐点的限制

目录：

穿插纸条 （第1-18关）交叉点计数 

穿插纸条 （第19-36关）双层覆盖的起点和终点 

穿插纸条 （第37-54关）解的不唯一性 

穿插纸条 （第55-72关）曼哈顿距离的奇偶性 

穿插纸条 （第73-90关）终点和连通性对于拐点的限制 

穿插纸条 （第91-108关）交叉点计数的极端情况

（74）

（75）

（76）

（77）

（78）

（79）

（80）

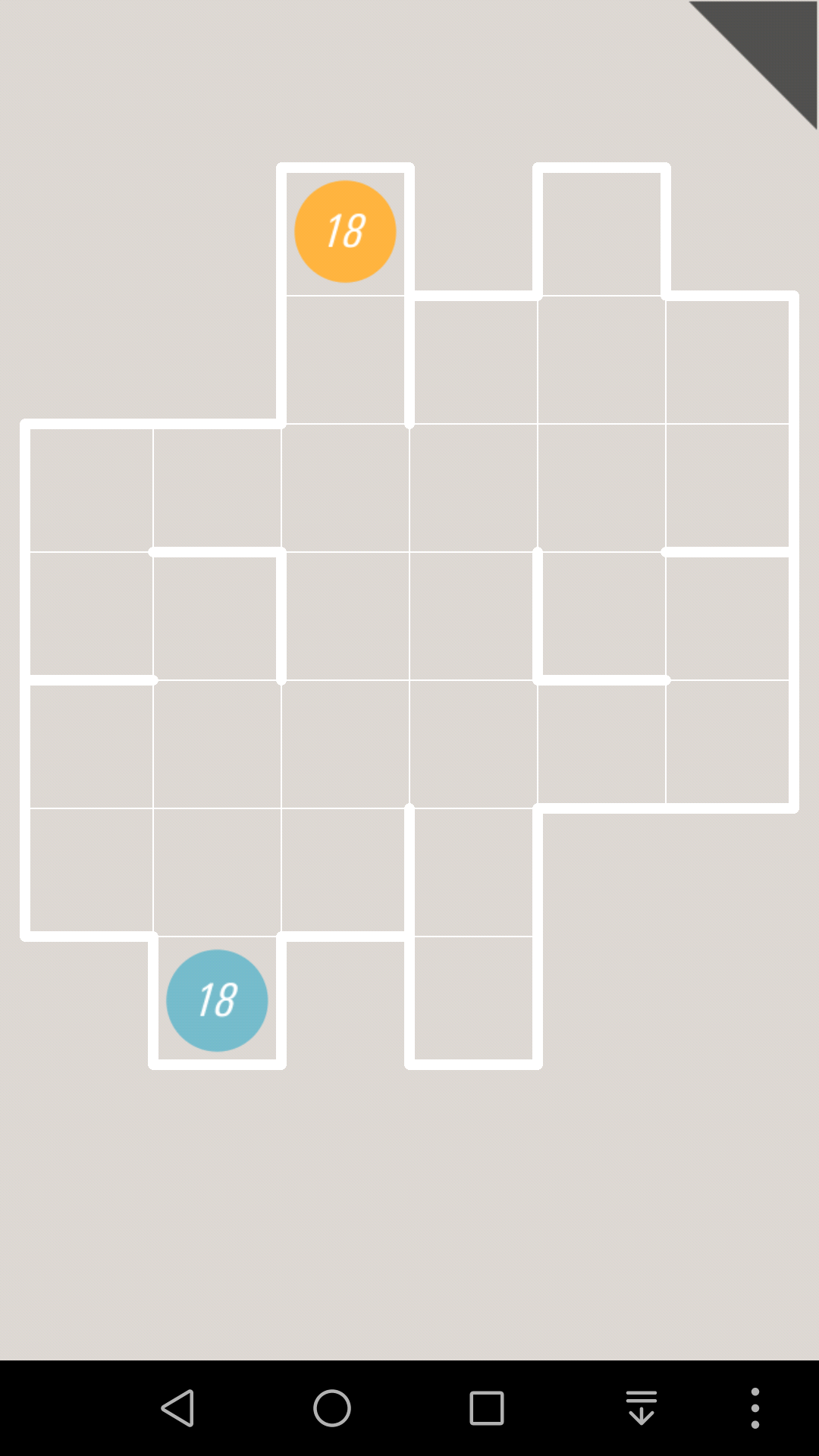
这里我引入终点对于拐点的限制

所谓拐点就是某根纸条在这个格子里面拐弯，拐点一定是单层覆盖。

在  穿插纸条 （第1-18关）交叉点计数 一文中我提到：

如果一个格子A只有一个相邻的格子，那么格子A就是某根纸条的终点。

实际上还可以拓展，因为拐点一定是单层覆盖，可以排出邻居的计算，所以不能随意产生拐点，否则会产生终点。

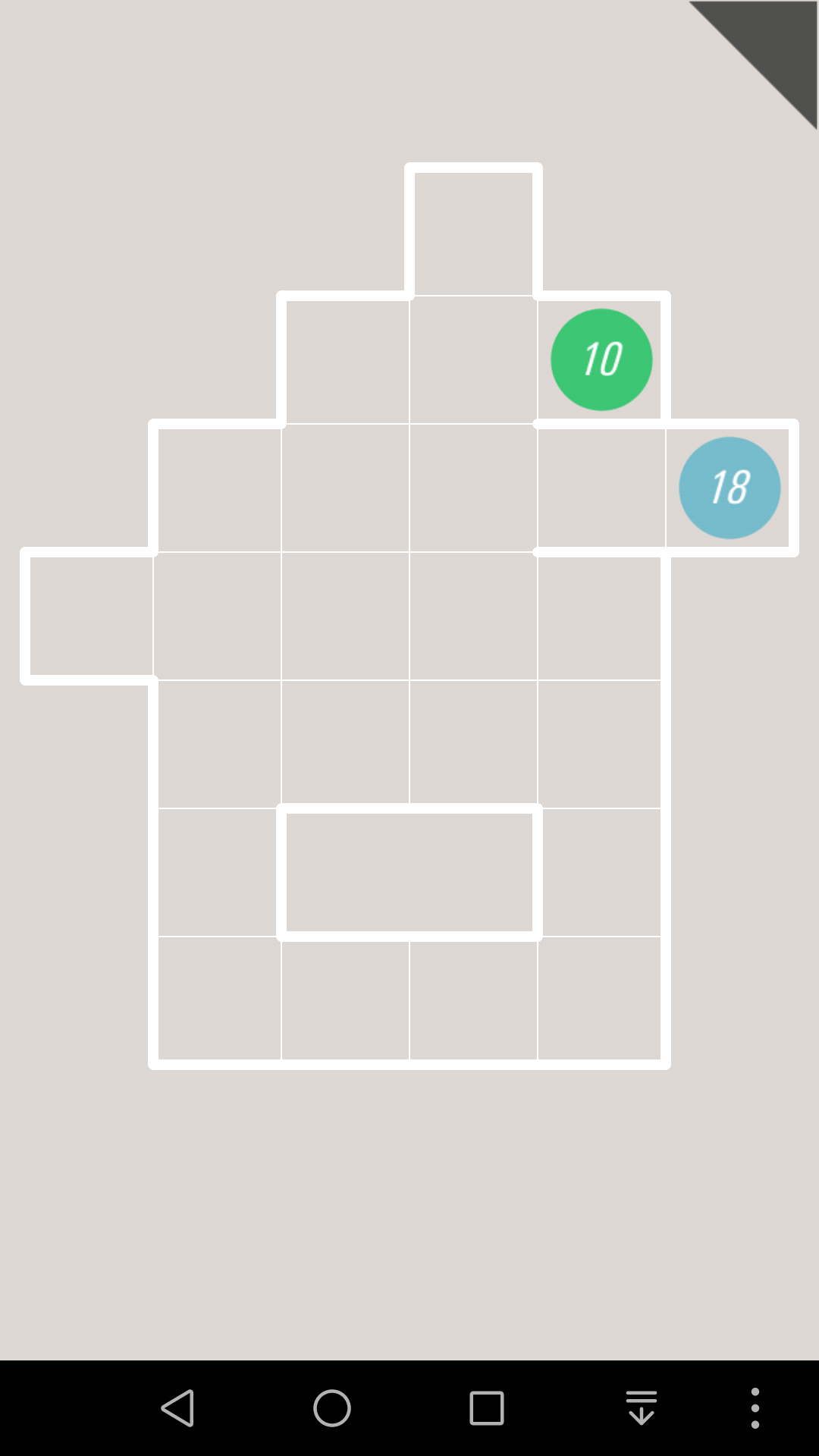
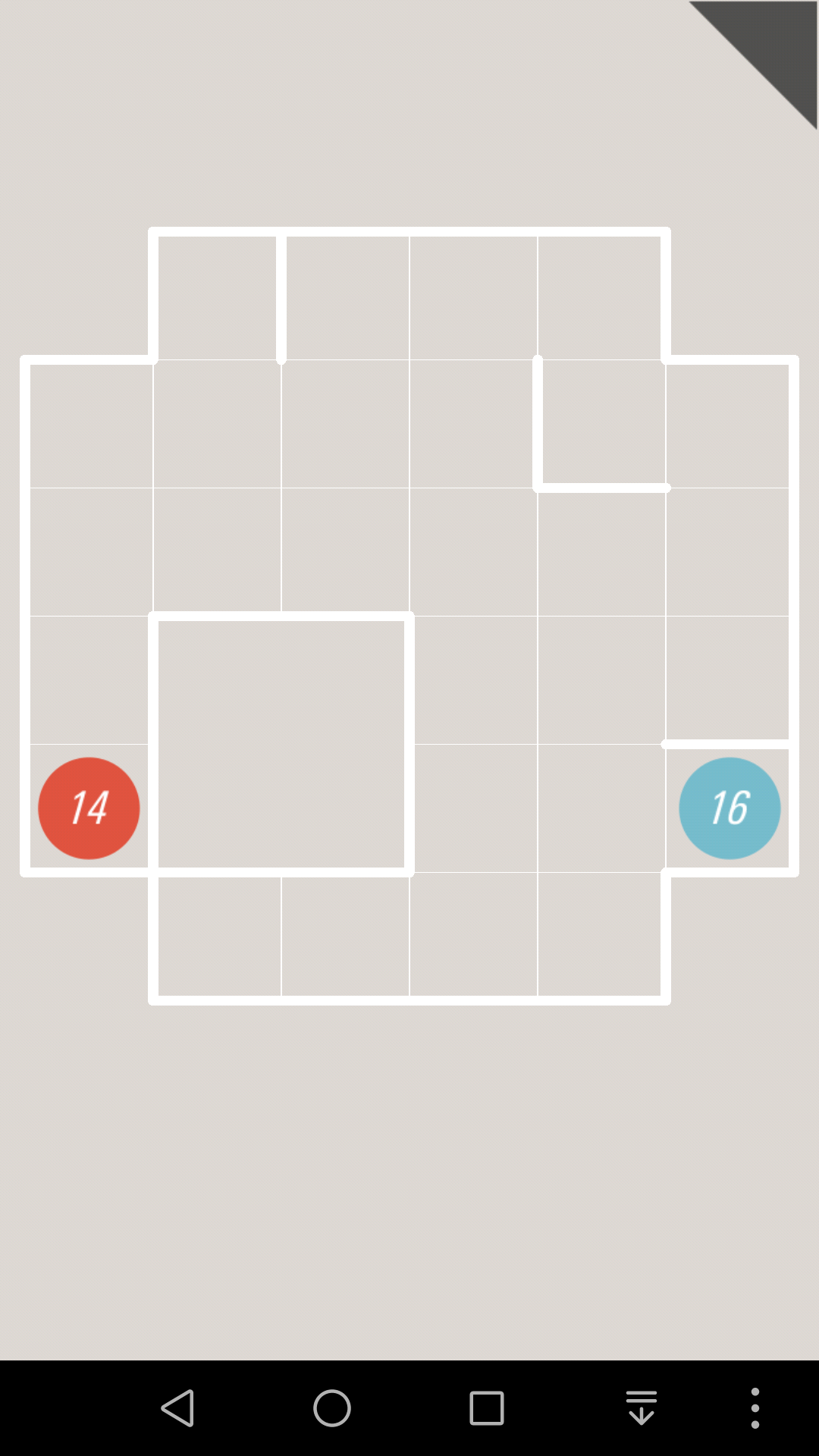
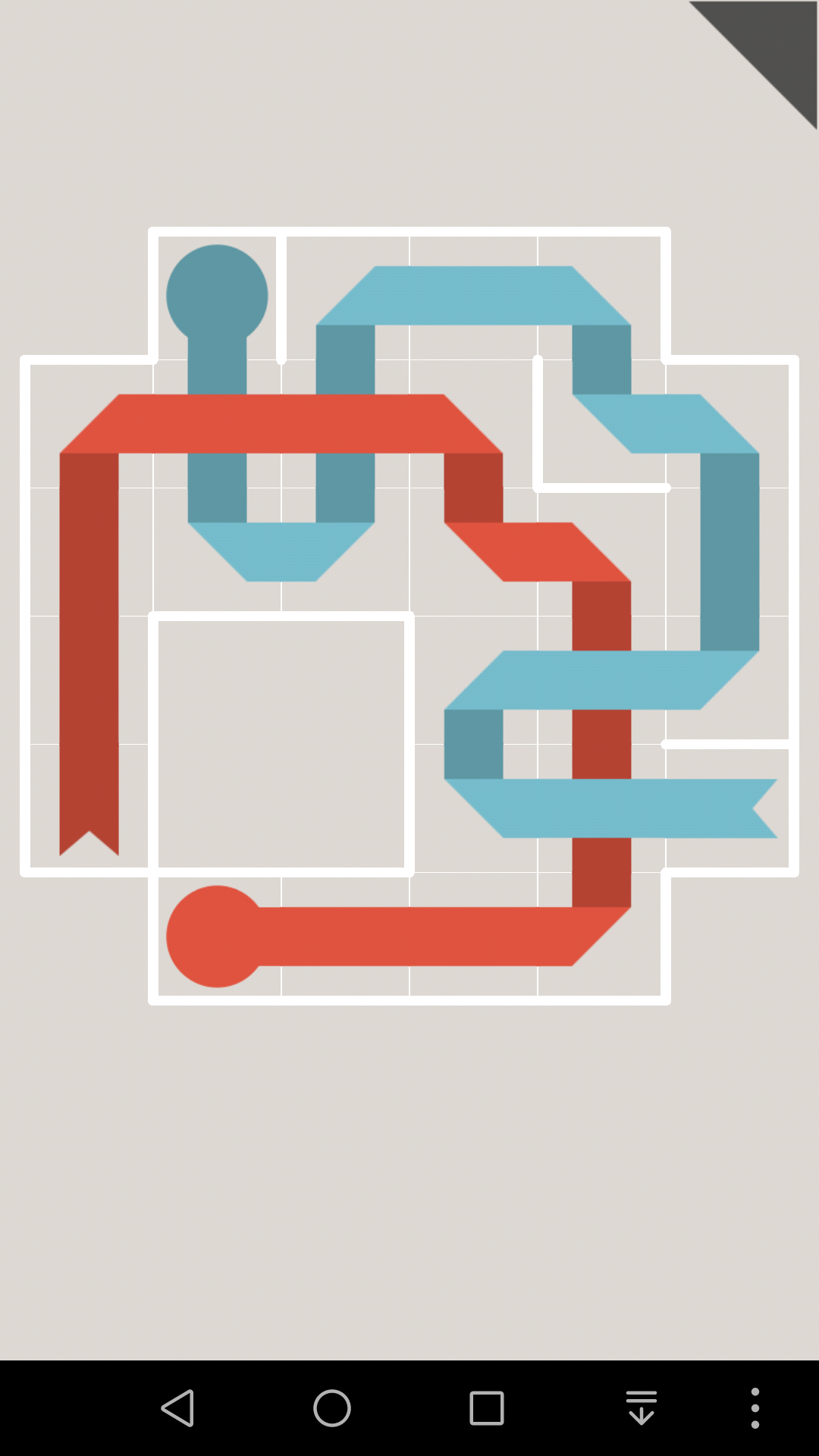
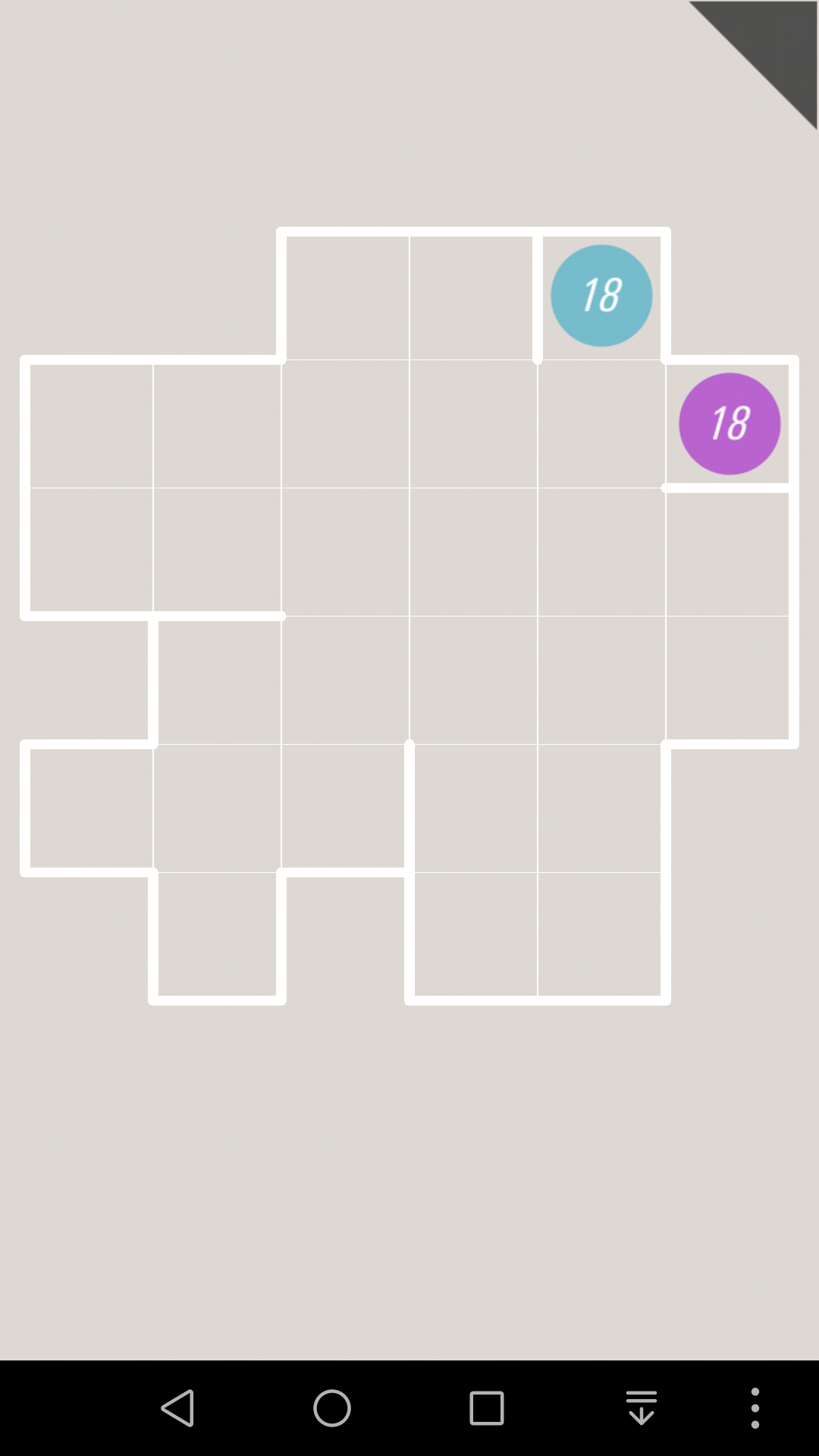
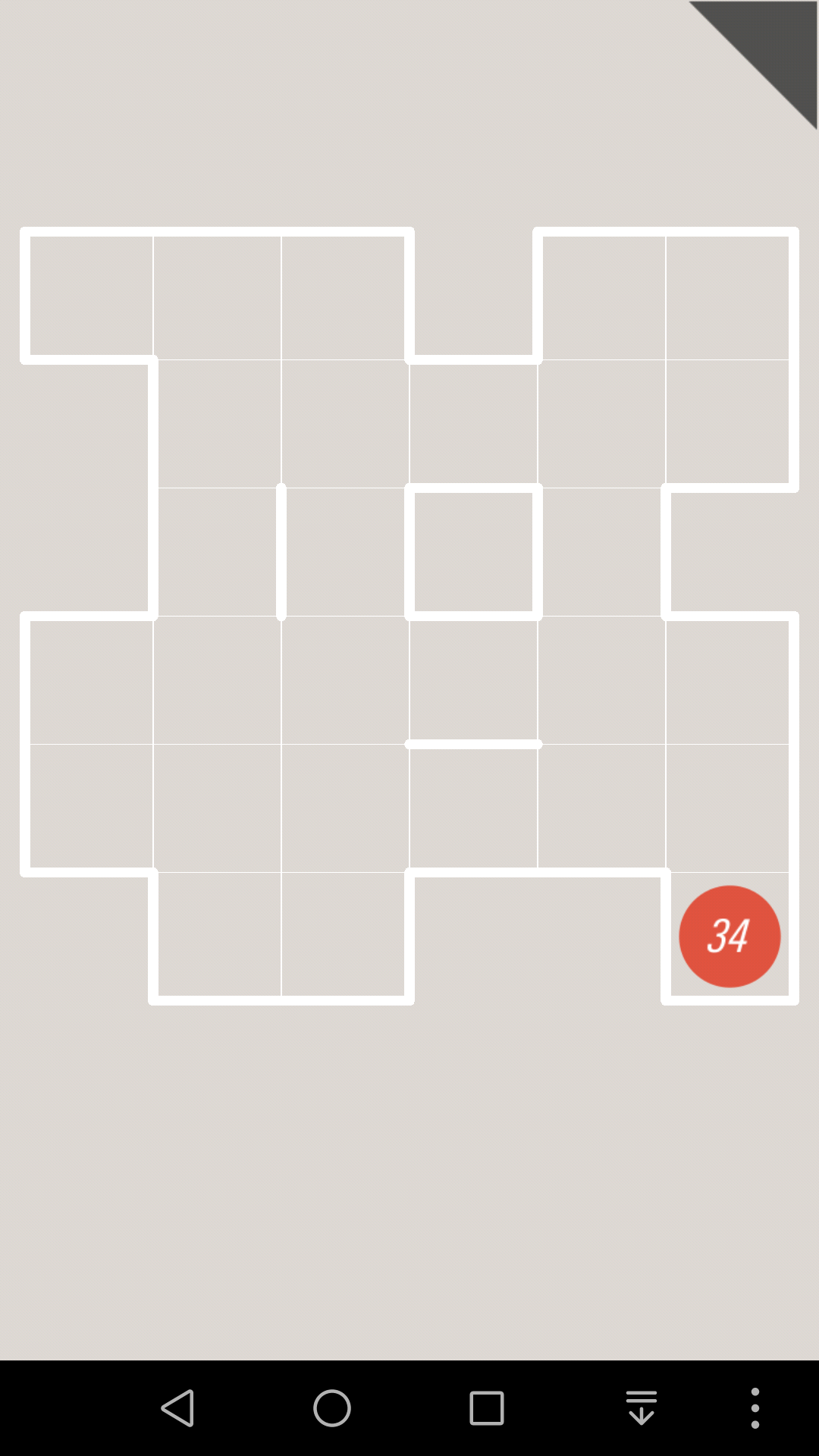
比如这一关，蓝色的18肯定首先是往上走

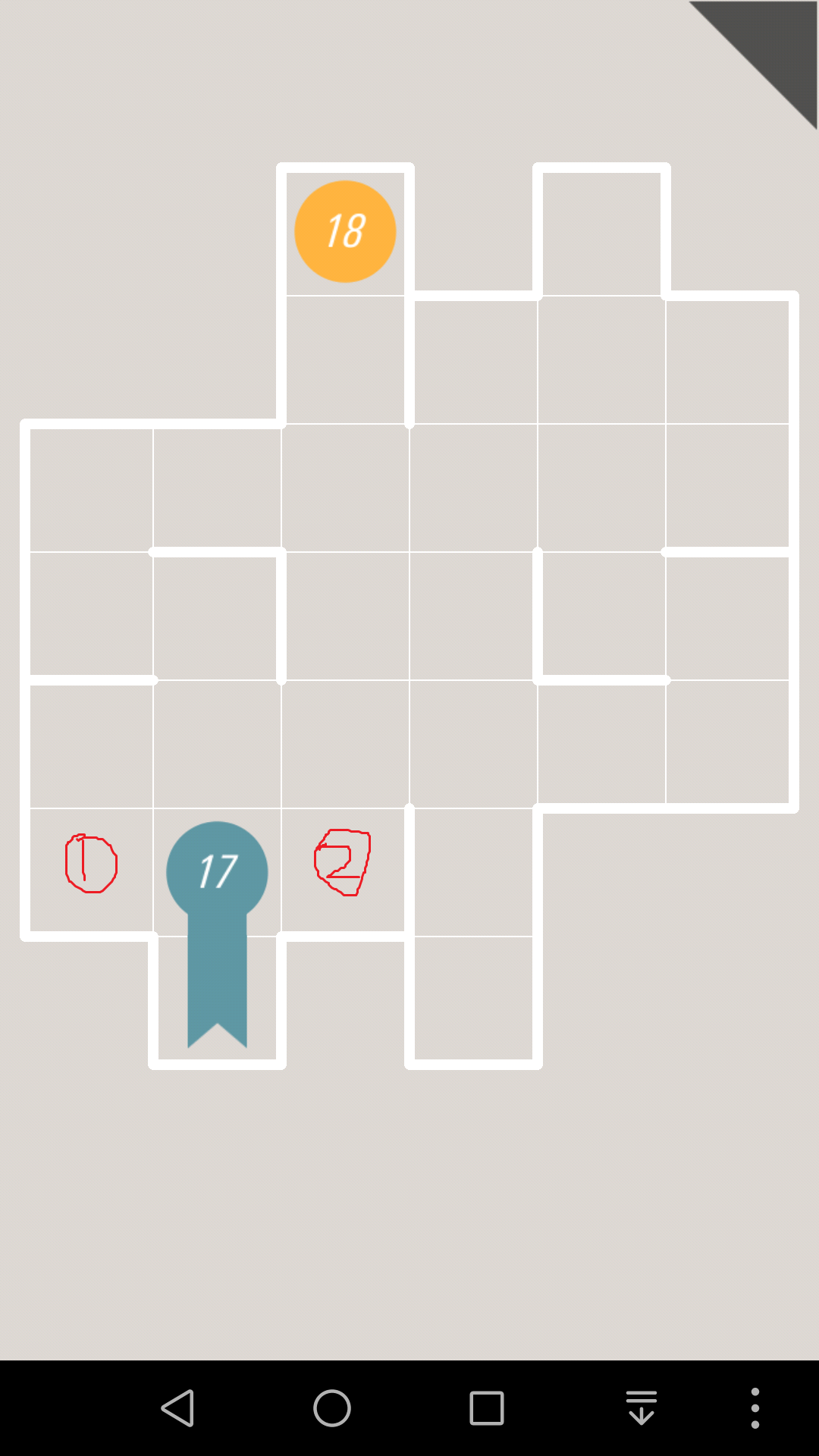
如果17往左走，2号格子就只有1个邻居了，所以就一定是终点，如果17往右走，1号格子就是终点。

然而2个终点的位置很明显，不是1号也不是2号，所以17接下来只能继续往上走

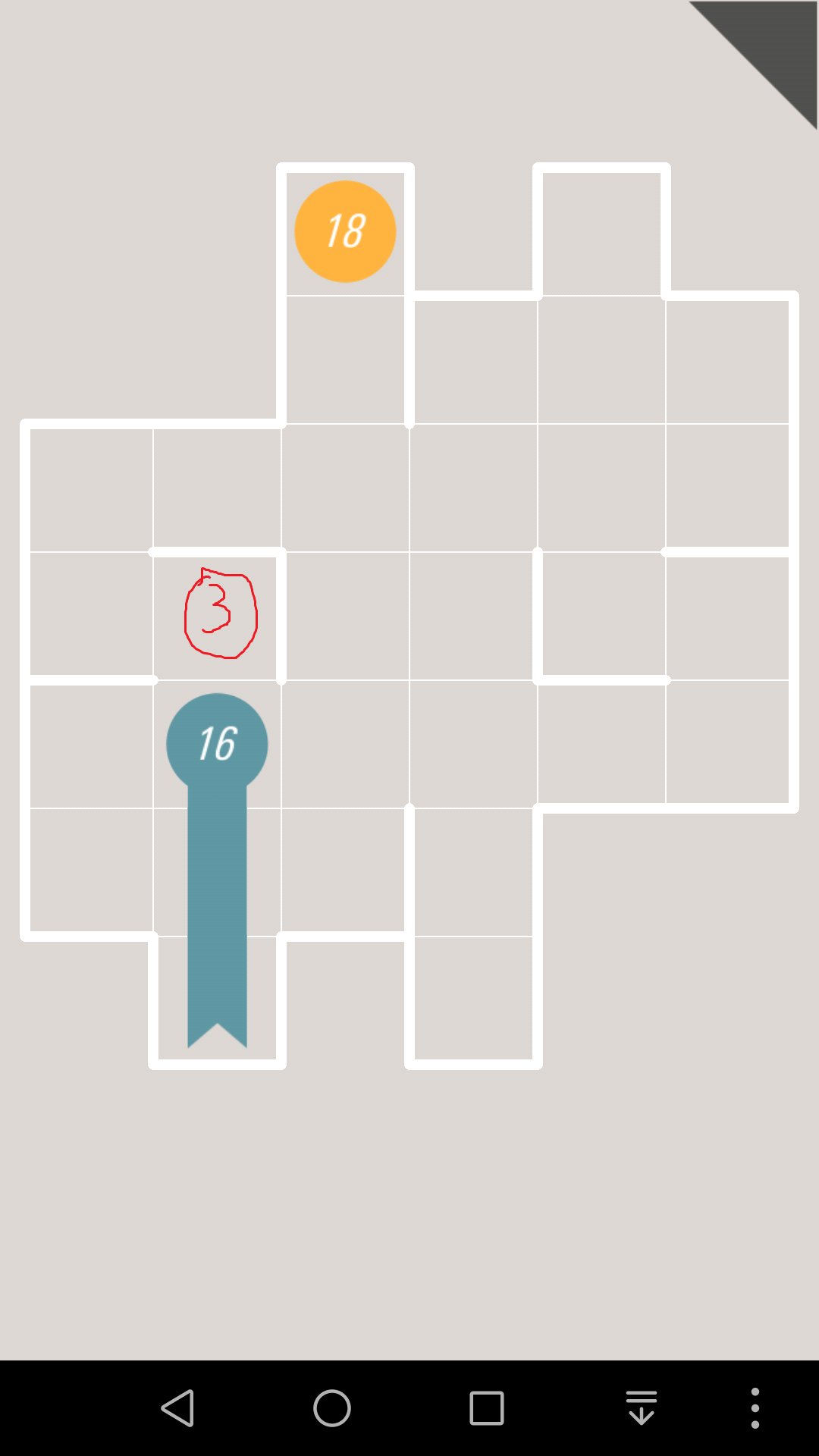
同理，3号格子不是终点，所以16在这里不能拐弯，也就是只能往上走

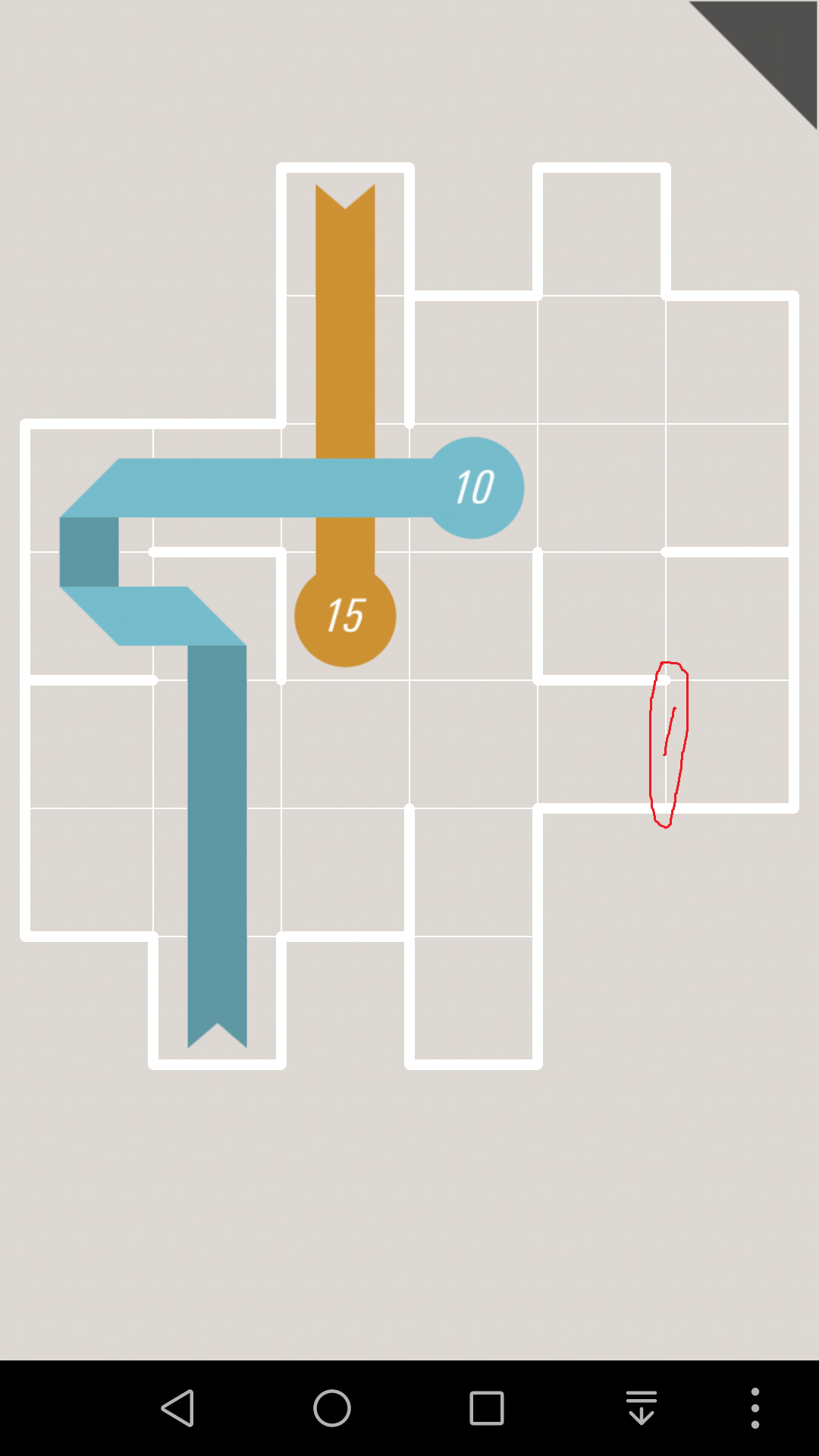
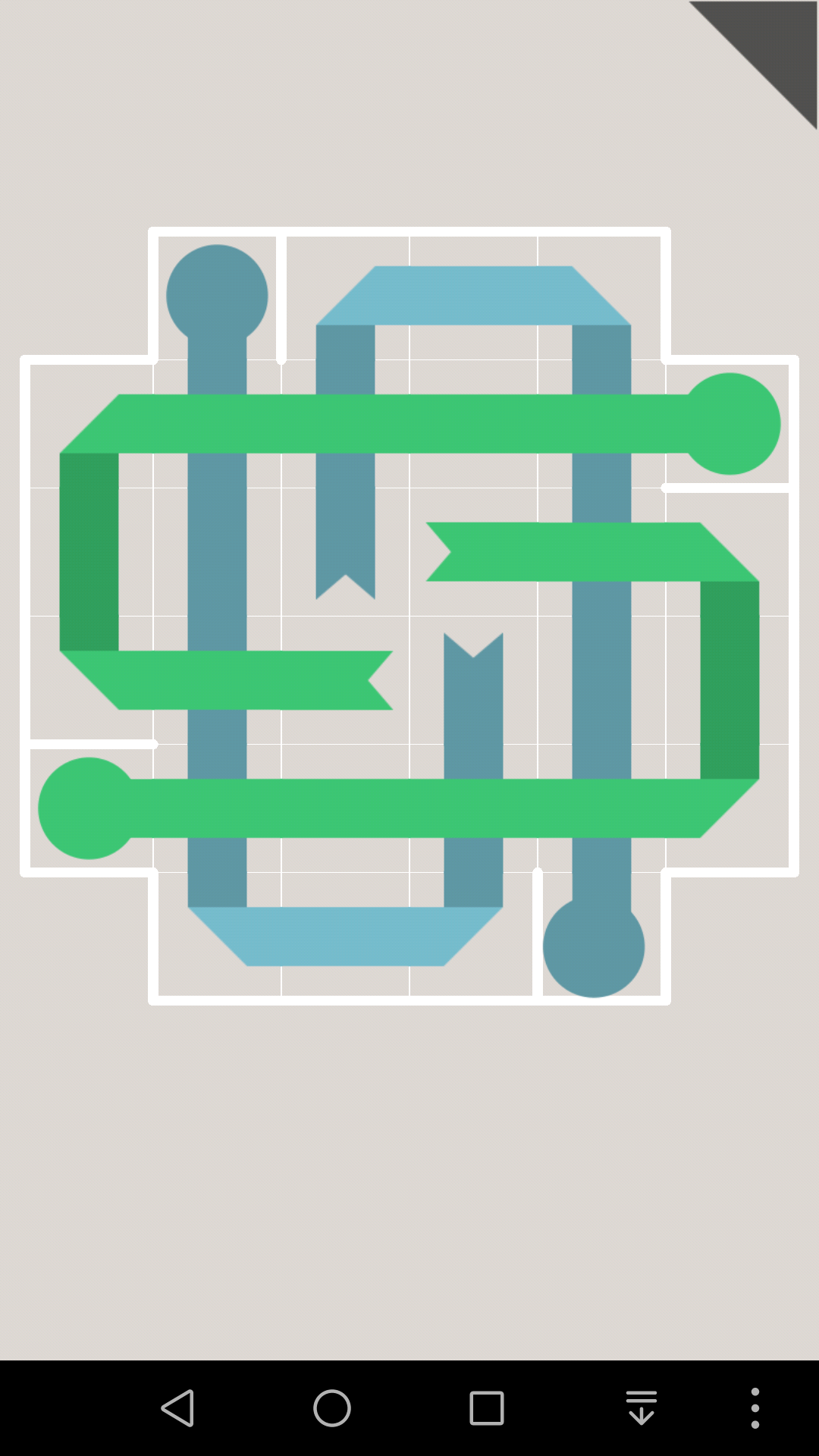
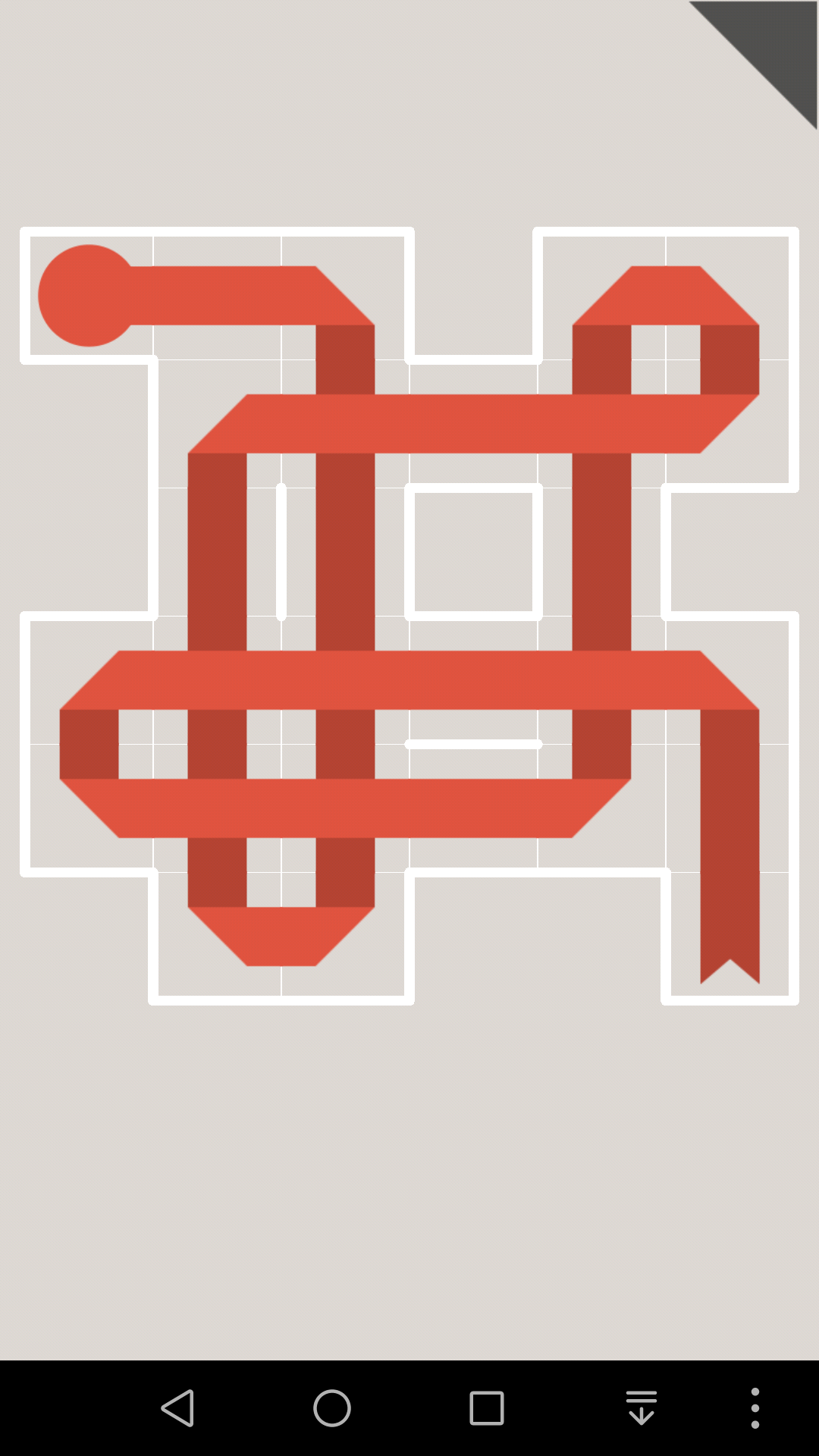
接着再引入连通性对于拐点的限制：

首先注意到，2个相邻格子的公共边，最多只会被1张纸条通过

其次，拐点一定是单层覆盖，这就会对连通性造成影响

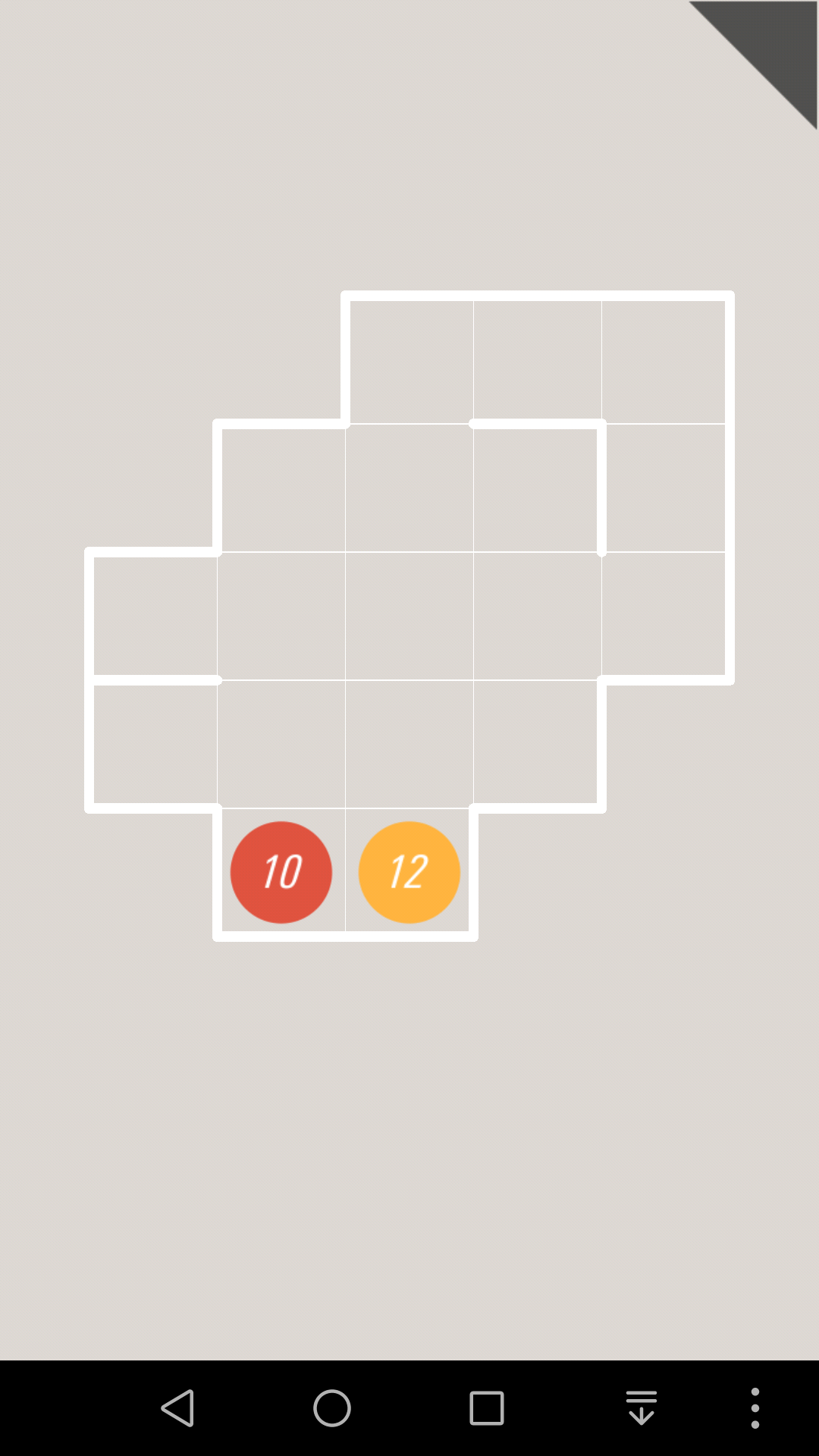
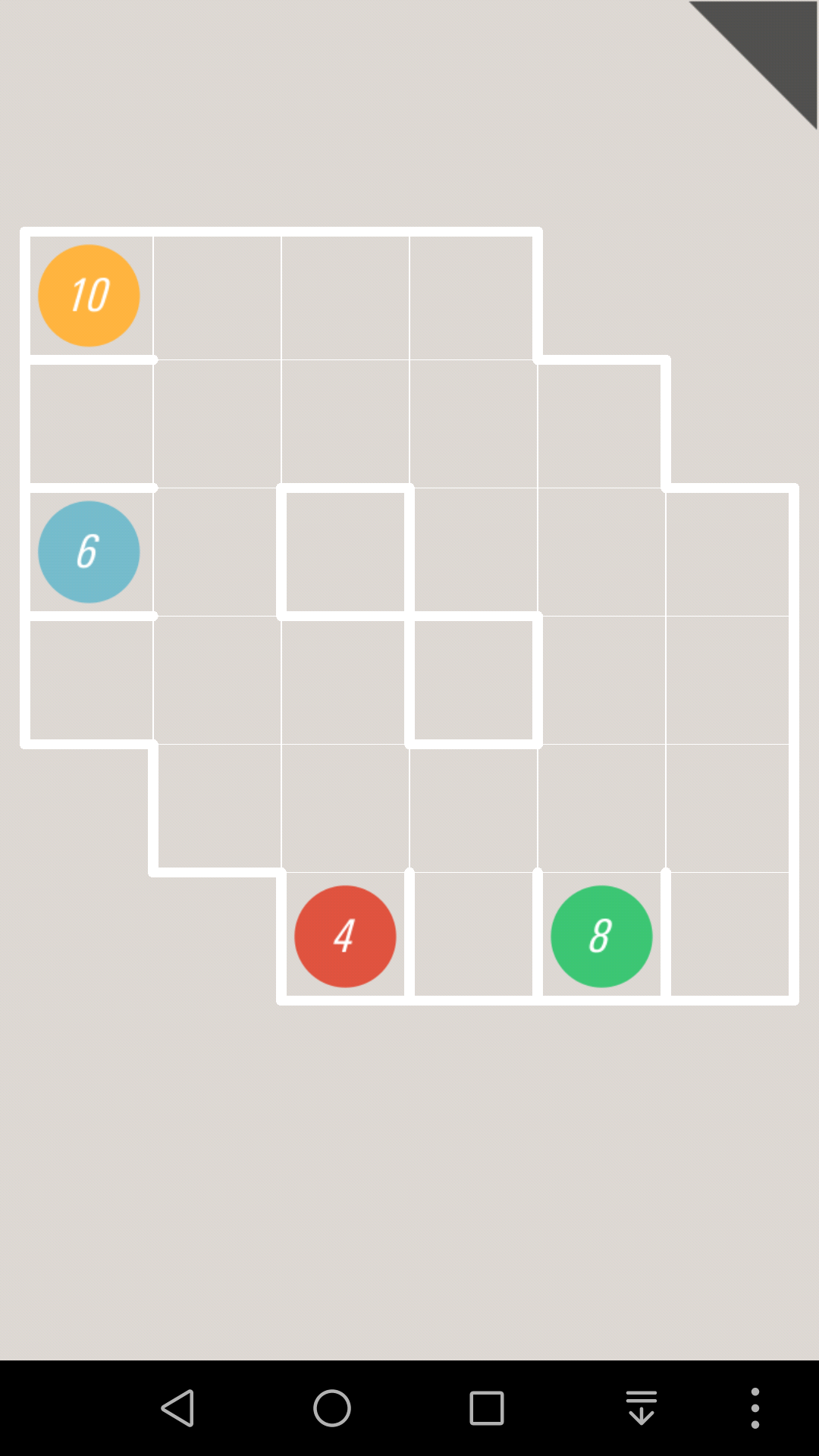
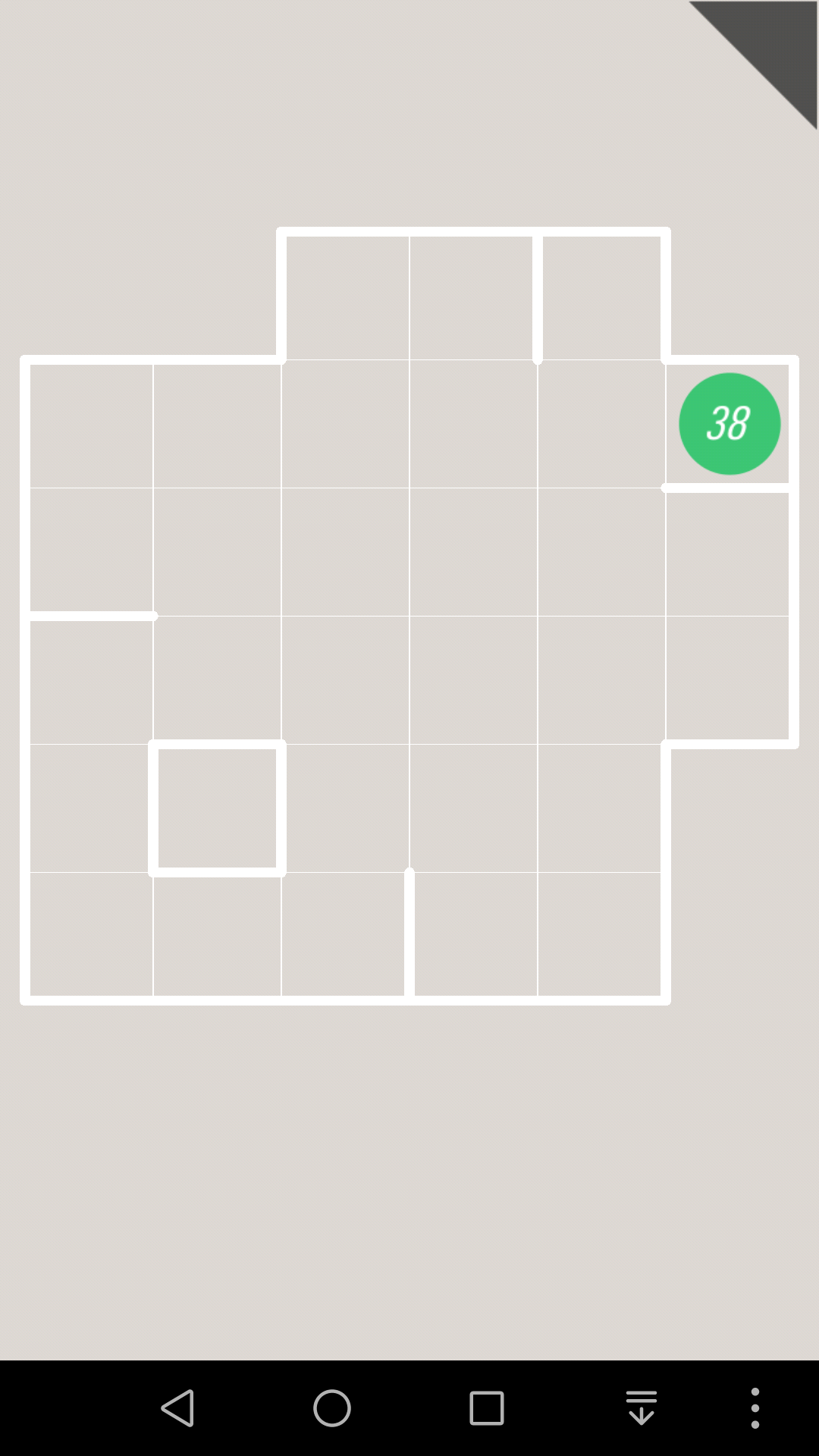
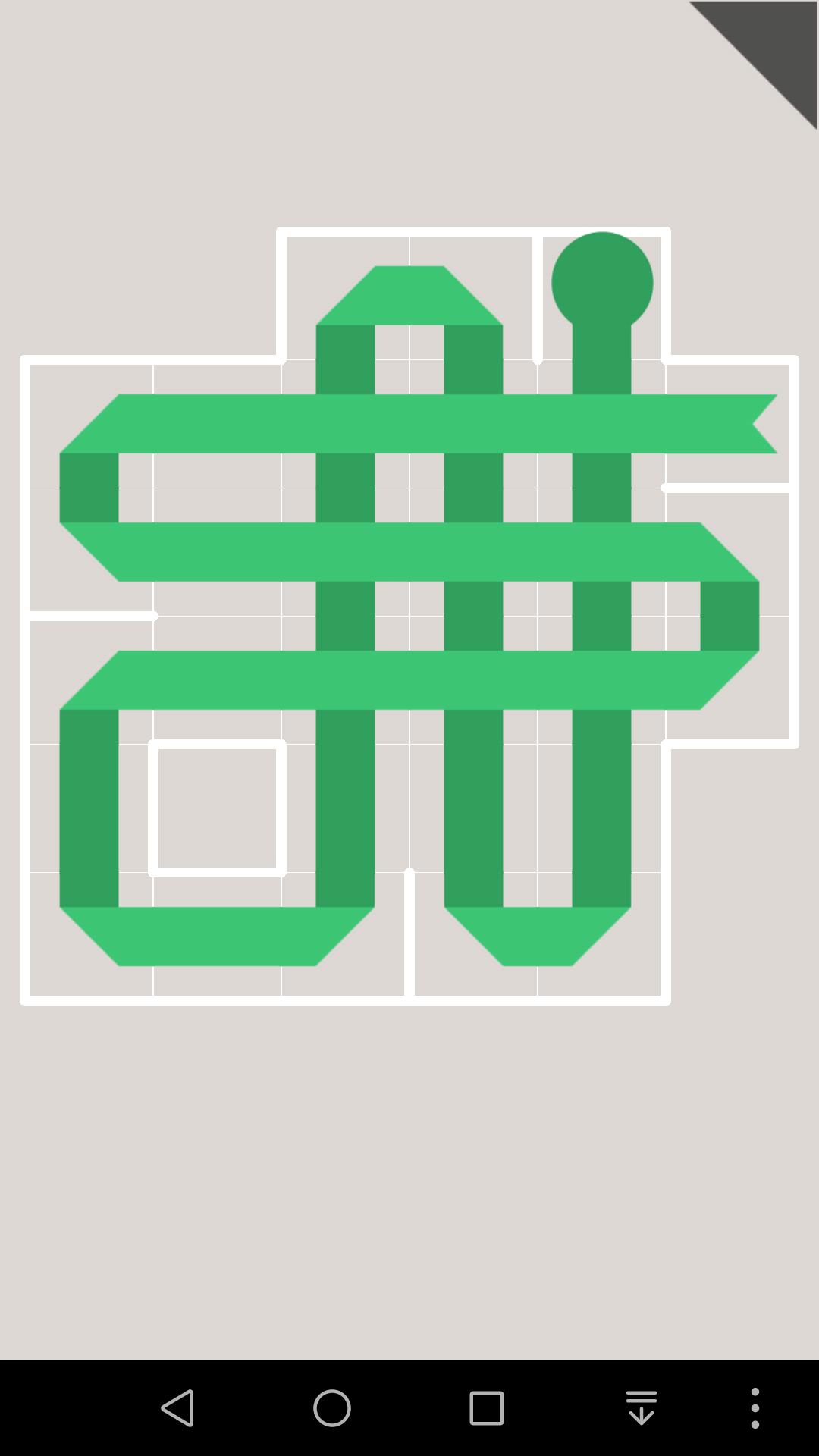
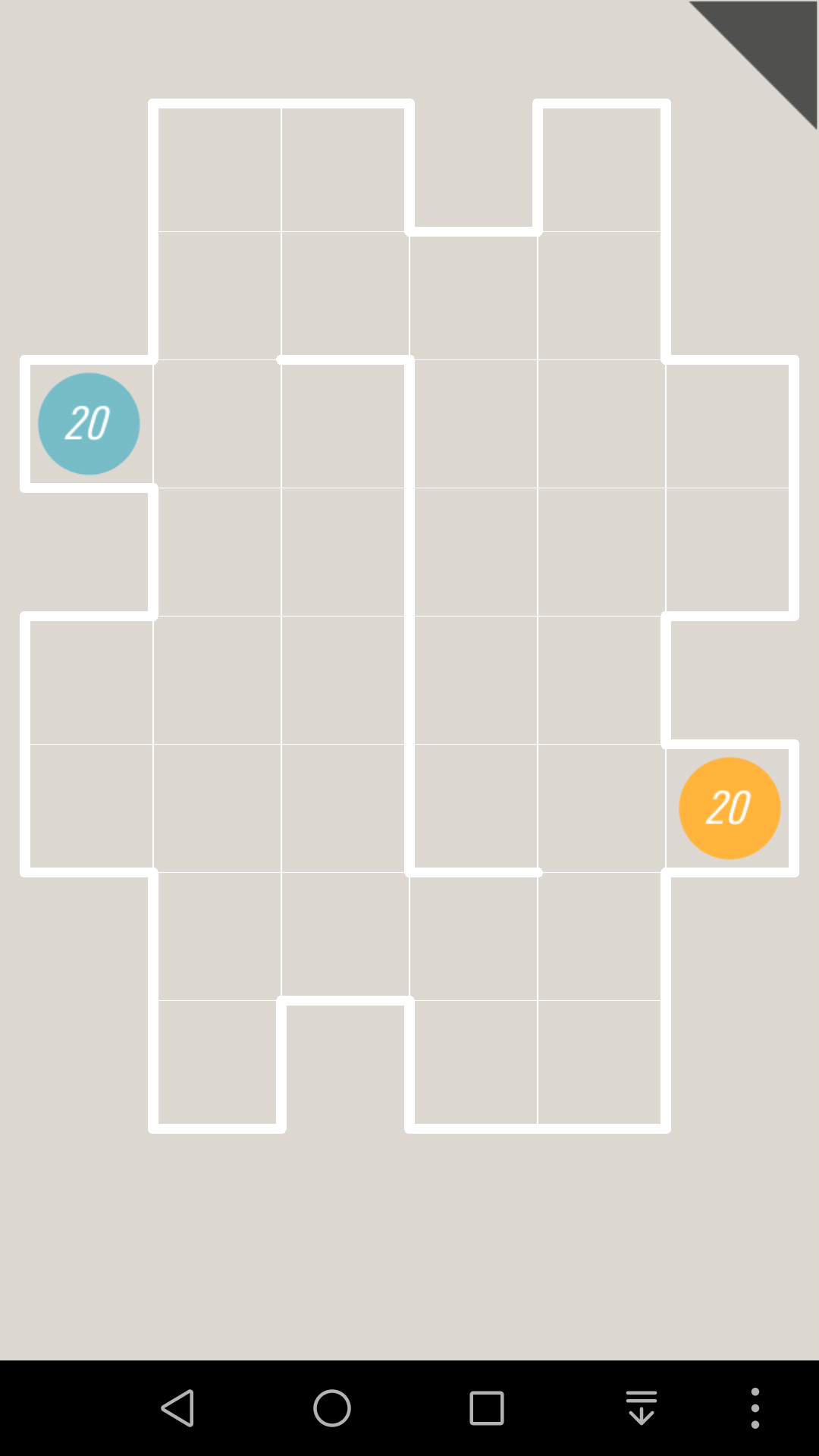
对于这一关，如果10往上走的话，那么10号格子就会堵死，那么1号边就会成为连通2个部分的唯一通道

因为黄色纸条的终点是右上那个，蓝色纸条的终点是下面那个，所以接下来黄色纸条和蓝色纸条都必须通过1号边，这是不可能的。

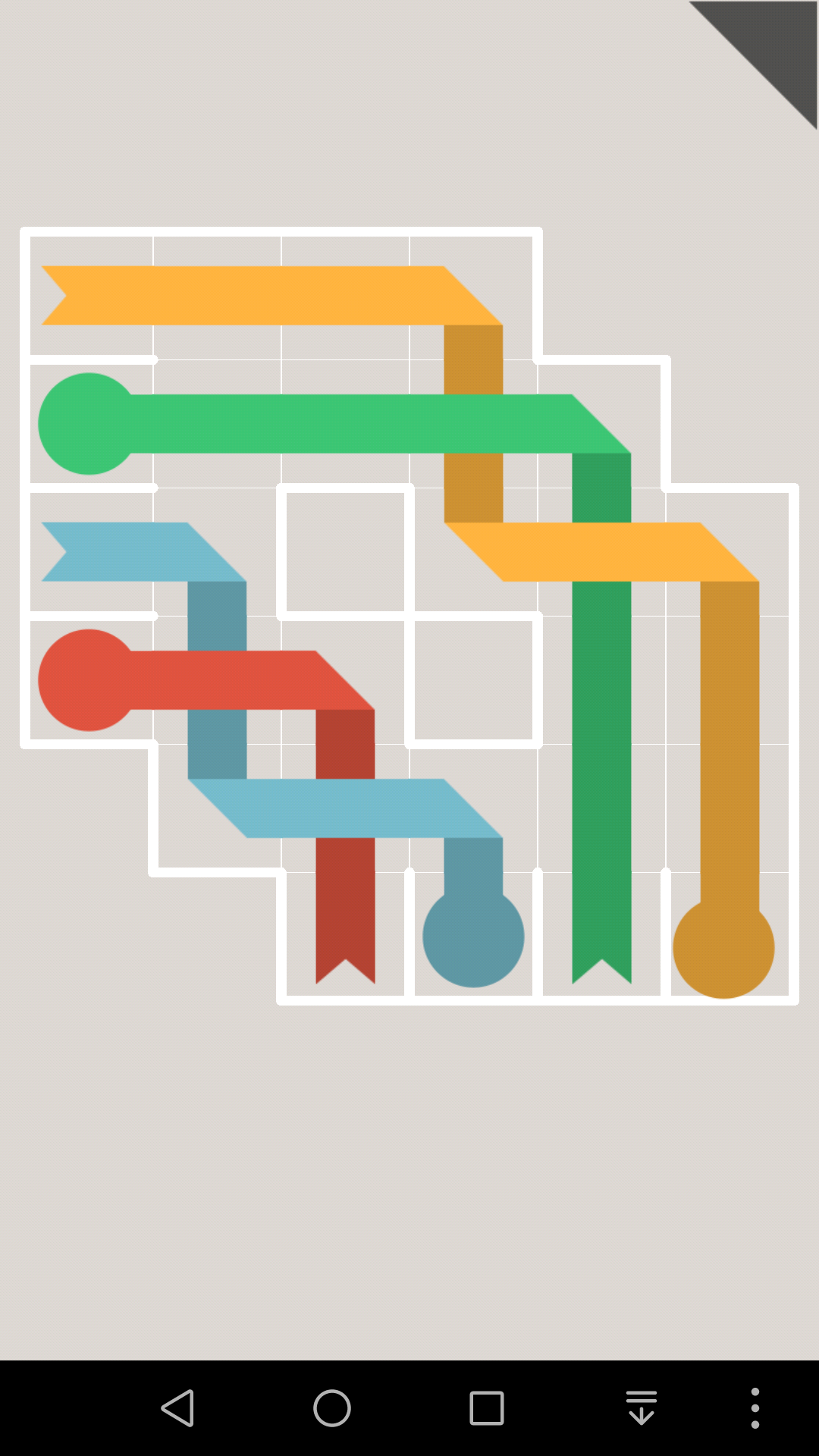
所以10只能往右走

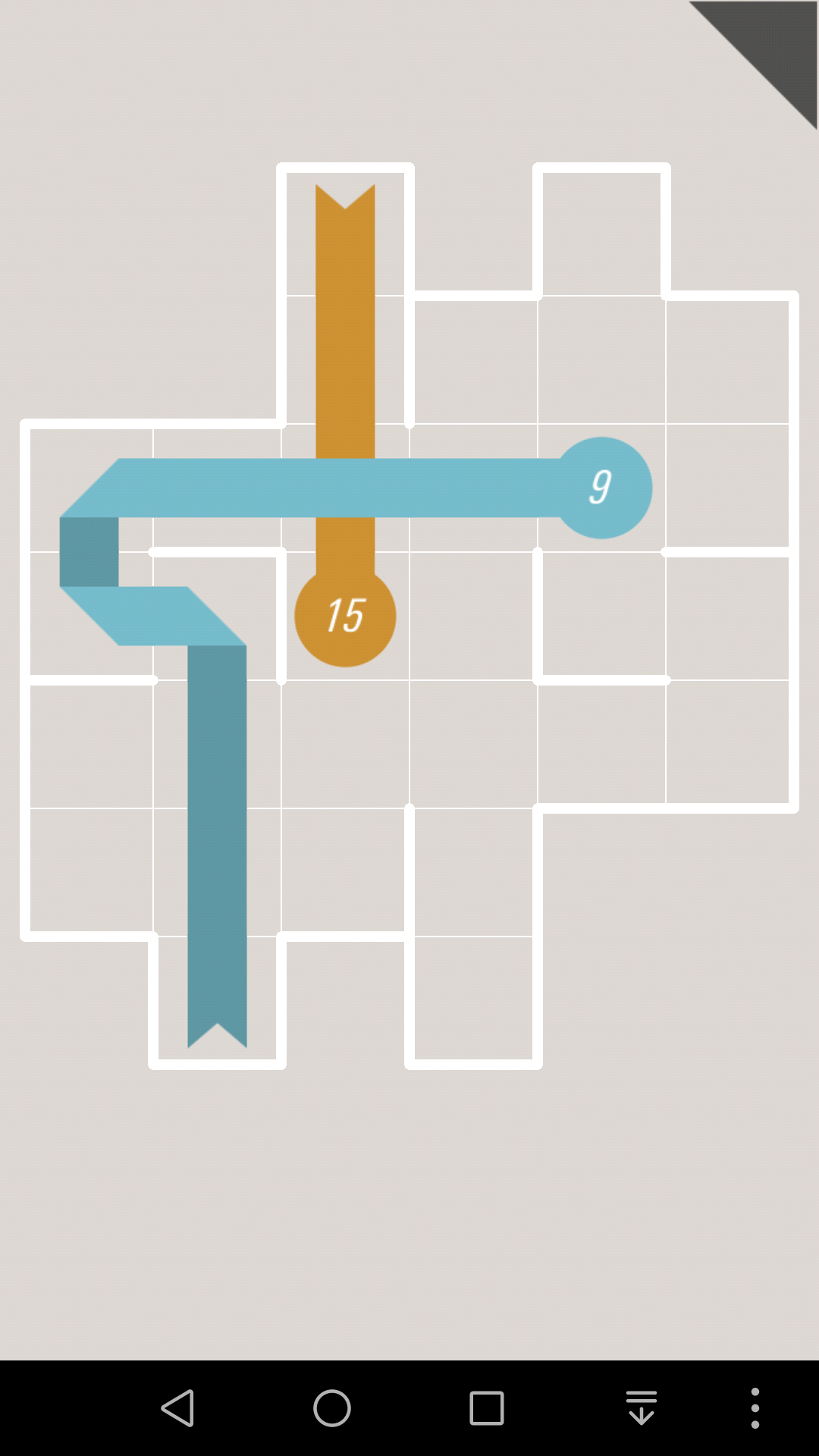
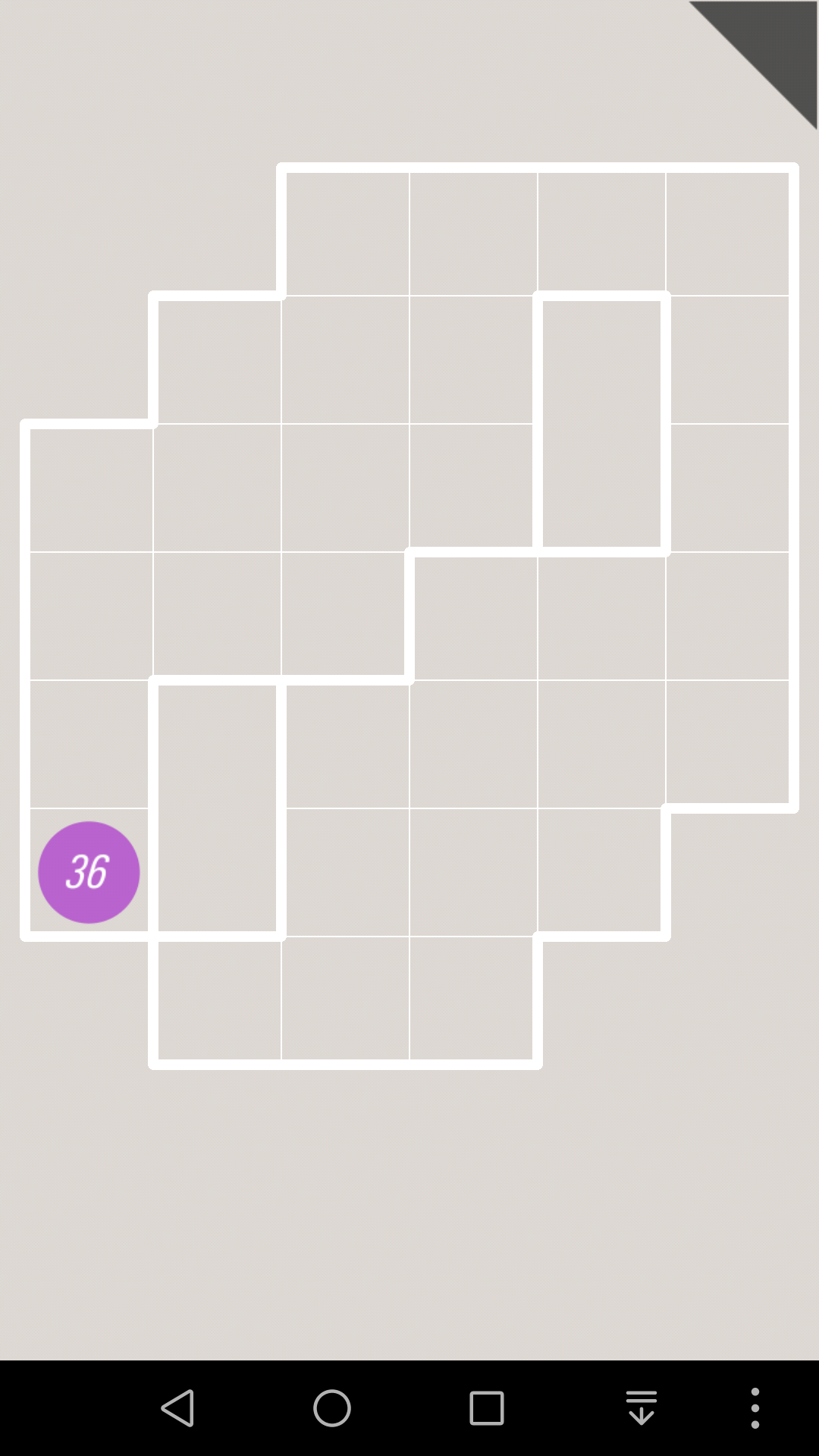
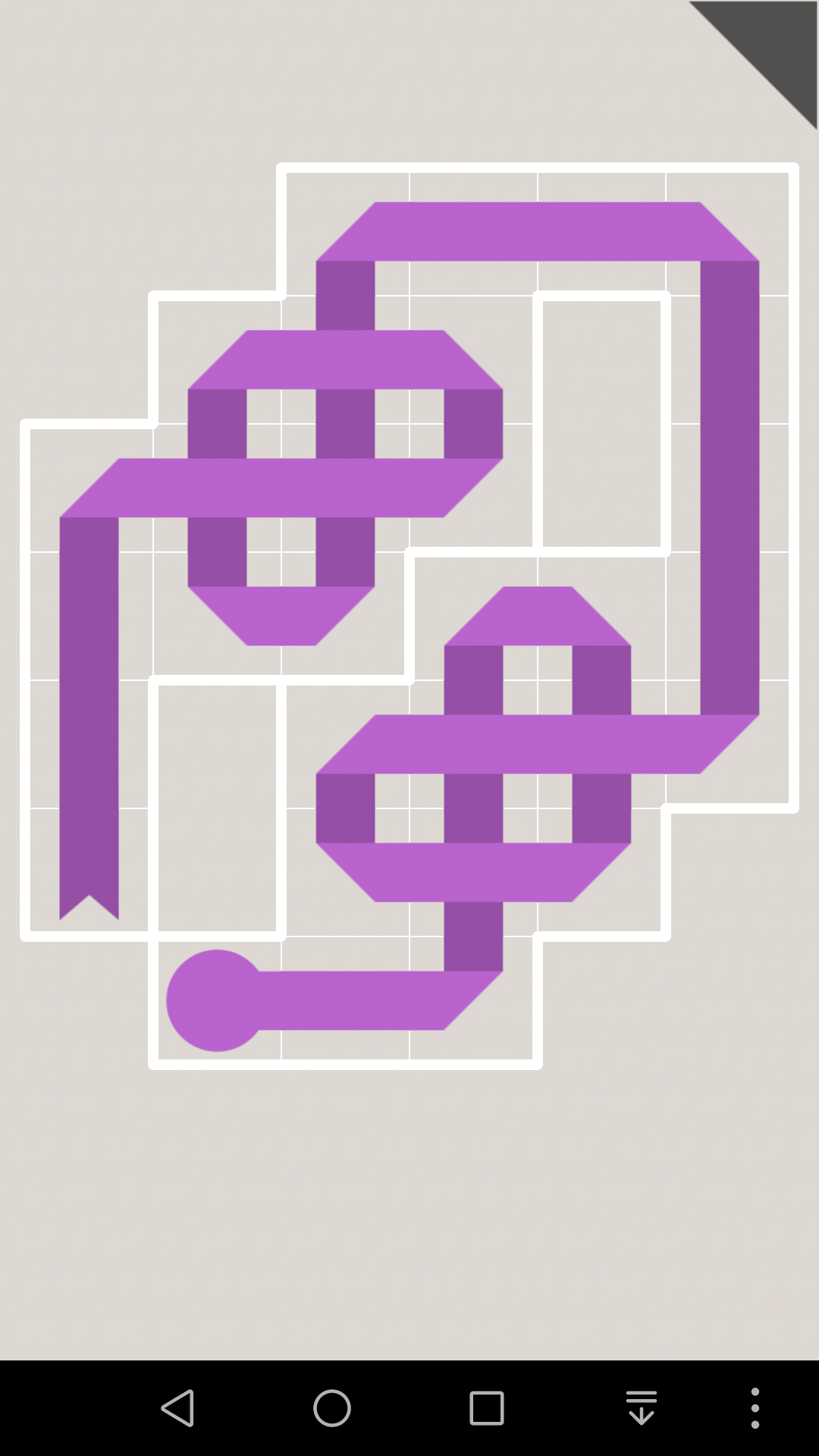
同理可以继续推出，这一关有唯一解

（81）

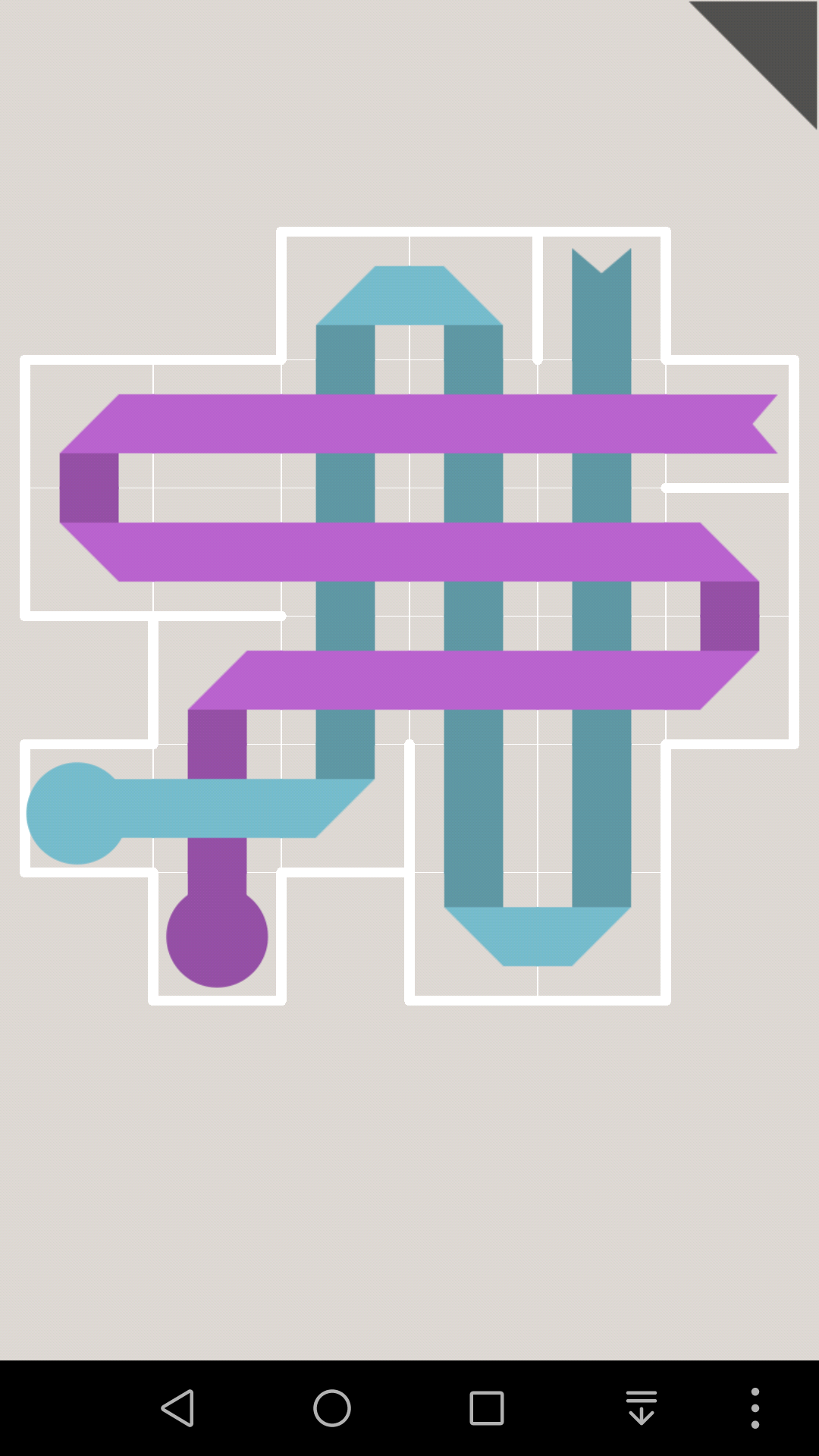
（82）

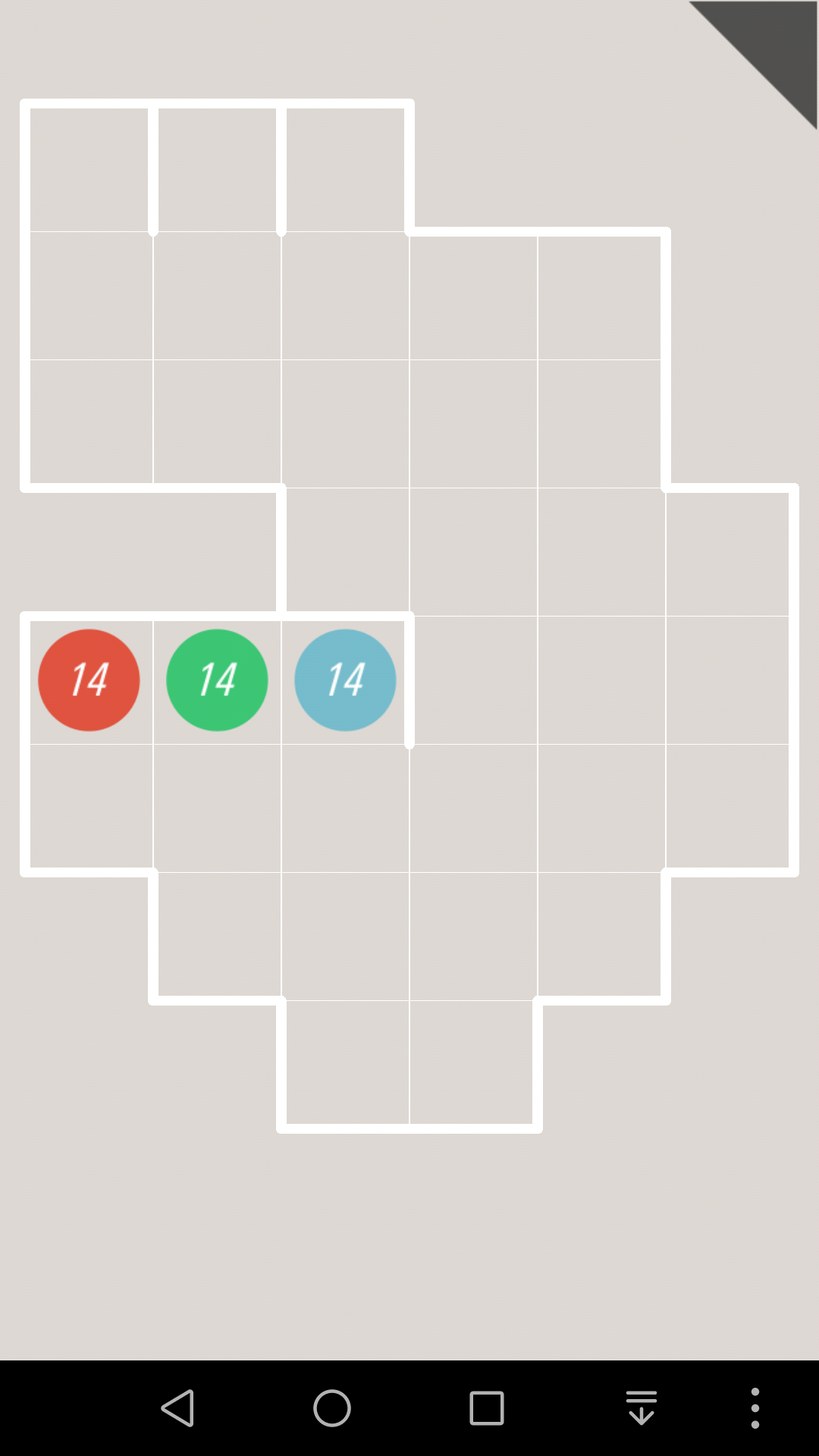
（83）

（84）

（85）

（86）

（87）

（88）

（89）

（90）

文章来源: blog.csdn.net，作者：csuzhucong，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/nameofcsdn/article/details/77969542