连续划分问题HDU - 1249 三角形
目录
一,连续划分问题
1,1维——线段 or 直线
n个点可以把线段或者直线分成多少段?
答案是 n+1
2,2维——圆形 or 整个平面
n个直线把圆或者平面分成多少块?
答案是(1+2+3+......+n)+1 = n(n+1)/2+1
3,2.5维——圆形
圆上的n个点,两两连接成的n(n-1)/2条弦最多可以把圆分成多少块?
思路:单点发出的n-1条弦被其他弦分割形成的分割点的个数是1*(n-3)+2*(n-4)+...+(n-4)*2+(n-3)*1=(n-1)(n-2)(n-3)/6
所以答案是 即n(n-1)(n-2)(n-3)/24+n(n-1)/2+1
即n(n-1)(n-2)(n-3)/24+n(n-1)/2+1
4,3维——球形 or 整个空间
n个平面把球形或者空间分成多少块?
答案是 
二,OJ实战
HDU - 1249 三角形
题目:
Description
用N个三角形最多可以把平面分成几个区域?
Input
输入数据的第一行是一个正整数T(1<=T<=10000),表示测试数据的数量.然后是T组测试数据,每组测试数据只包含一个正整数N(1<=N<=10000).
Output
对于每组测试数据,请输出题目中要求的结果.
Sample Input
2
1
2
Sample Output
2
8
解释一下网上到处飞的递推式f(n)=f(n-1)+(n-1)*6是怎么来的。
这个问题其实和n条直线可以把平面分成多少个部分是差不多一样的。
对于直线的问题,递推式是f(n)=f(n-1)+n
也就是说,从n-1条直线,变成n条直线,多了n块。
为什么就刚好是n呢?因为,一条直线可以被n-1条直线分成n段,而每一段,都恰好对应着从n-1条直线变成n条直线时会有1块变成2块,于是整体增加了n块。
对于三角形的问题,道理是一样的。
一个三角形(注意,这里指的是三条边构成的曲线)可以被n-1个三角形分成(n-1)*6段,于是便得到了递推式。
所以f(n)=3 * n*(n - 1) + 2
代码:
-
#include<iostream>
-
using namespace std;
-
-
int main()
-
{
-
int k, n;
-
cin >> k;
-
while (k--)
-
{
-
cin >> n;
-
cout << 3 * n*(n - 1) + 2 << endl;
-
}
-
return 0;
-
}
HDU - 2050 折线分割平面
题目:
我们看到过很多直线分割平面的题目,今天的这个题目稍微有些变化,我们要求的是n条折线分割平面的最大数目。比如,一条折线可以将平面分成两部分,两条折线最多可以将平面分成7部分,具体如下所示。
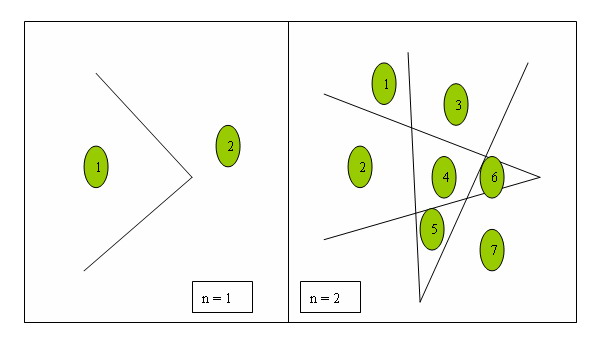
Input
输入数据的第一行是一个整数C,表示测试实例的个数,然后是C 行数据,每行包含一个整数n(0<n<=10000),表示折线的数量。
Output
对于每个测试实例,请输出平面的最大分割数,每个实例的输出占一行。
Sample Input
2
1
2
Sample Output
2
7
这个问题的本质,和直线分割平面问题是一样的。
每增加1个折线,增加的平面区域的数目等于增加的交点的数目加1
每2个折线都可以有4个交点,如此便得到公式
代码:
-
#include<iostream>
-
using namespace std;
-
-
int main()
-
{
-
int a;
-
cin >> a;
-
while (cin >> a)cout << a*a * 2 - a + 1 << endl;
-
return 0;
-
}
51Nod - 1104 直线分割圆
圆上有N个点,每个点和其他所有点之间都有直线相连。并且任意3线不共点。计算这些直线把圆分割所得的区域的数量K。
例如:N = 2,K = 2,N = 3,K = 4。由于结果可能会很大,输出K Mod (10^9 + 7)的结果。
Input
输入:1个数N。(2 <= N <= 10^9)
Output
输出数量 Mod 10^9 + 7
Sample Input
2
Sample Output
2
-
#include<iostream>
-
using namespace std;
-
-
int main()
-
{
-
long long n,p=1000000007;
-
cin>>n;
-
long long x=n*(n-1)/2%p,y=(n-2)*(n-3)/2%p;
-
long long z=x*y%p*(p+1)/6%p+x+1;
-
cout<<z%p;
-
return 0;
-
}
文章来源: blog.csdn.net,作者:csuzhucong,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/nameofcsdn/article/details/115914119
- 点赞
- 收藏
- 关注作者


评论(0)