- 微信
- 微博
  
  分享文章到微博
- 复制链接
  
  复制链接到剪贴板

生日问题

用户已注销发表于 2021/11/19 03:17:29 2021/11/19

【摘要】目录一，生日问题二，一般性生日问题三，相关问题四，函数值估算一，生日问题 In probability theory, the birthday problem or birthday paradox concerns the probability that, in a set of n randomly ch...

一，生日问题

In probability theory, the birthday problem or birthday paradox concerns the probability that, in a set of n randomly chosen people, some pair of them will have the same birthday. In a group of 23 people, the probability of a shared birthday exceeds 50%, while a group of 70 has a 99.9% chance of a shared birthday.

23个人的生日全都不同的概率是 $(1-frac{1}{366})(1-frac{2}{366})...(1-frac{22}{366})$ ，约等于50%

70个人的生日全都不同的概率是 $(1-frac{1}{366})(1-frac{2}{366})...(1-frac{69}{366})$ ，约等于0.1%

二，一般性生日问题

在一个有k个不同元素的集合中，不放回地取n个数，全都不同的概率是 $(1-frac{1}{k})(1-frac{2}{k})...(1-frac{n-1}{k})$

设 $p(n)=(1-frac{1}{k})(1-frac{2}{k})...(1-frac{n}{k})$ ，则全都不同的概率可以表示成p(n-1)

$p(0)=1, p(1)=1-frac{1}{k}, ...,, p(k-1)=(1-frac{1}{k})(1-frac{2}{k})...(1-frac{k-1}{k}),, p(k)=0$

分别求出3个求求和式：f、g、h

令 $f(n)=sum_{t=1}^np(t)=sum_{t=1}^n(1-frac{1}{k})(1-frac{2}{k})...(1-frac{t}{k})$ ,

$f(0)=1, f(1)=1-frac{1}{k}, , ...,,f(k-1)=sum _{t=1}^{k-1}p(t), ,, f(k)=f(k-1)$

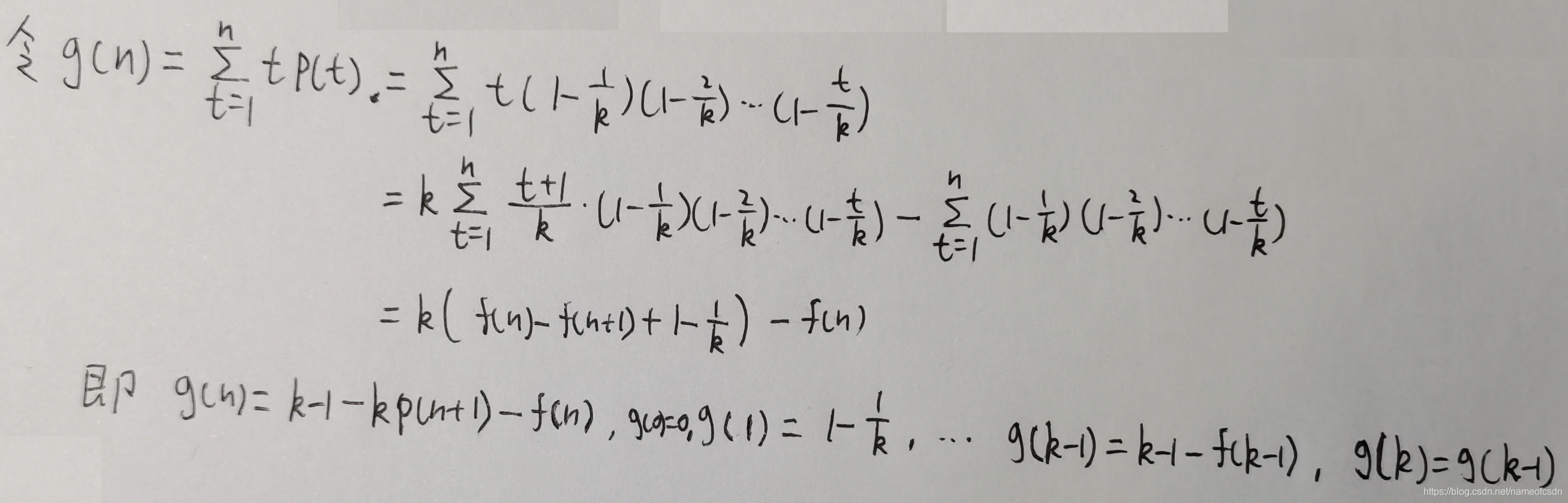
三，相关问题

在一个有k个不同元素的集合中，不放回地取数，一直到第一次出现重复的数为止，取数的数目（包括最后这个重复的数）的均值是多少呢？

$E=sum _{t=2}^{k+1}p(t-2)frac{t-1}{k}t=frac{h(k-1)+3g(k-1)+f(k-1)+2}{k}$

所以 $E=(1-frac{1}{k})f(k-1)+2$ ，其中 $f(k-1)=sum _{t=1}^{k-1}p(t)$

所以 $E=2+(1-frac{1}{k})sum _{t=1}^{k-1}(1-frac{1}{k})(1-frac{2}{k})...(1-frac{t}{k})$

四，函数值估算

$p(n)=(1-\frac{1}{k})(1-\frac{2}{k})...(1-\frac{n}{k})<e^{-\frac{1}{k}}e^{-\frac{2}{k}}...e^{-\frac{n}{k}}=e^{-\frac{n(n+1))}{2k}}$

$f(n)=sum_{t=1}^np(t)=sum_{t=1}^n(1-frac{1}{k})(1-frac{2}{k})...(1-frac{t}{k})$

令，

$f(k-1)< \sum _{t=1}^u 1+\sum _{t=u+1}^{k-1}(1-\frac{1}{k})(1-\frac{2}{k})...(1-\frac{t}{k})\\ <u+\sum _{t=u+1}^{k-1}(1-\frac{1}{k})(1-\frac{2}{k})...(1-\frac{u+1}{k})(1-\frac{u+1}{k})^{t-u-1}\\ <u+\frac{k}{u+1}(1-\frac{1}{k})(1-\frac{2}{k})...(1-\frac{u+1}{k})\\ <u+\frac{k}{u+1}e^{-\frac{(u+1)(u+2)}{2k}}$