一、函数概述

• 函数是学习C语言的重点。学习C语言有两个知识点是必须要学的，一个是函数，另一个是指针，这两个知识点是C语言的主体和核心，由此可见其重要性。虽然其它语言中也有函数，但是C语言中的函数更加重要。因为C语言中的函数与现在所有流行语言中的函数的用法都不太一样。学完C语言的函数有助于我们理解什么是面向过程。等将来学习面向对象语言，如 C++、Java 或者C#的时候就会发现，这些语言中函数的用法与C语言中的用法有很大的差别。因此，函数是理解面向过程和面向对象的切入点。通过 C 语言的函数可以直观地辨别出面向过程和面向对象的区别。C 语言的函数有一个特点，就是它有固定的格式和固定的模型。
• C语言是结构化程序设计语言，采用模块化的处理方式，每一个模块其实就是一个函数。对于比较复杂的问题，采用自顶向下，逐层分解，直到分解到最基本的模块，这就是结构化程序设计的基本方法。

二、函数的声明、定义与调用

（一）函数使用三步曲

1. 声明函数（只有函数头：函数名、形式参数、返回值）
2. 定义函数（包含函数头和函数体）
3. 调用函数（通过函数名加实际参数来调用）

• 其中，形式参数只能是变量（简单变量或数组变量），实际参数可以是常数、变量或者表达式。

（二）案例演示 - 编写函数求三个整数最大值

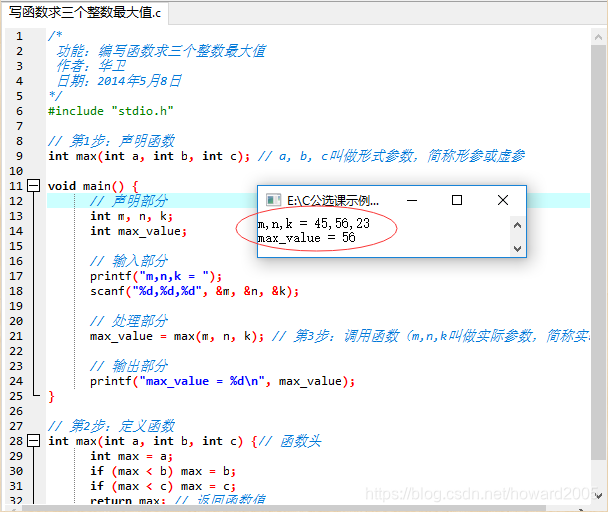
1、编写程序 - 编写函数求三个整数最大值.c

/* 
 功能：编写函数求三个整数最大值 
 作者：华卫
 日期：2014年5月8日
*/
#include "stdio.h"

// 第1步：声明函数
int max(int a, int b, int c); // a, b, c叫做形式参数，简称形参或虚参

void main() {
      // 声明部分
      int m, n, k;
      int max_value;
      
      // 输入部分
      printf("m,n,k = ");
      scanf("%d,%d,%d", &m, &n, &k);     
      
      // 处理部分
      max_value = max(m, n, k); // 第3步：调用函数（m,n,k叫做实际参数，简称实参）
      
      // 输出部分
      printf("max_value = %d\n", max_value);
}

// 第2步：定义函数
int max(int a, int b, int c) {// 函数头
      int max = a;      
      if (max < b) max = b;
      if (max < c) max = c;            
      return max; // 返回函数值
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
 

2、运行程序，查看结果

（三）课堂练习 - 计算阶乘之和

• 编写阶乘函数计算0! + 1! + 2! + …… + 10!。
  
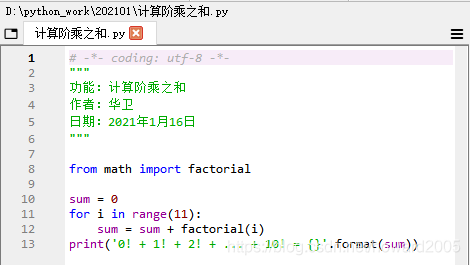
• 编写程序 - 计算阶乘之和.py
  
• 运行程序，查看结果
  

三、参数传递

（一）值传递

1、概述

当调用函数传入的实际参数是常量、简单变量或表达式，此时采用值传递的方式，也就是实际参数的值传给形式参数后，不会受形式参数变化的影响。值传递是一种单向的数据传递。

当实际参数是常量或表达式的时候，值传递很好理解，只是把数据传给形式参数就了事，不会接受形式参数变化的影响。因此，我们只演示实际参数是变量时的值传递。

2、案例演示

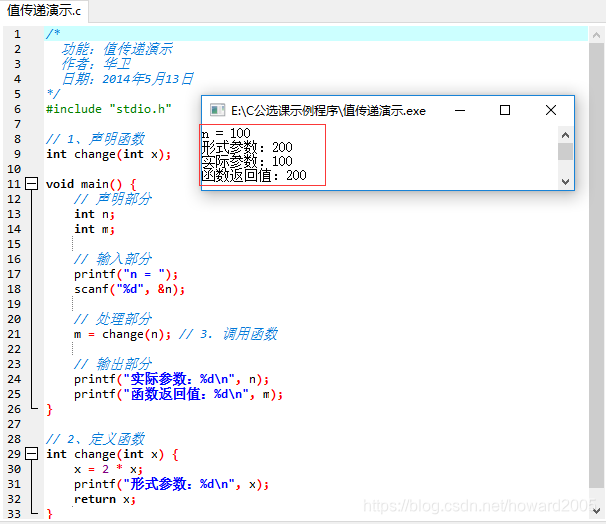
• 编写程序 - 值传递演示.c

/* 
  功能：值传递演示
  作者：华卫
  日期：2014年5月13日
*/
#include "stdio.h"

// 1、声明函数
int change(int x);

void main() {
      // 声明部分
      int n;        
      int m; 
      
      // 输入部分
      printf("n = ");
      scanf("%d", &n);
      
      // 处理部分
      m = change(n); // 3. 调用函数
      
      // 输出部分
      printf("实际参数：%d\n", n);
      printf("函数返回值：%d\n", m);
}

// 2、定义函数
int change(int x) {
      x = 2 * x;
      printf("形式参数：%d\n", x);
      return x;   
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
 

• 运行程序，查看结果
  

（二）地址传递

1、概述

当调用函数传入的实际参数是数组时，采用地址传递方式，也就是说形式参数（数组）值发生变化，会反过来影响实际参数（数组）。地址传递是一种双向传递。

2、案例演示

• 编写程序 - 地址传递演示.c

/* 
  功能：地址传递演示
  作者：华卫
  日期：2014年5月13日
*/
#include "stdio.h"

// 1、声明函数
void reverse(int a[], int n);

void main() {
      // 声明部分
      int i; // 循环变量        
      int b[10] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
      
      // 输出部分
      printf("原序：");
      for(i = 0; i < 10; i++) {
            printf("%d ", b[i]);
      }      
      printf("\n");
      
      // 处理部分
      reverse(b, 10); // 3、调用函数：实际参数是一个数组，采用地址传递方式
      
      // 输出部分
      printf("反序：");
      for(i = 0; i < 10; i++) {
            printf("%d ", b[i]);
      }           
}

// 2、定义函数（功能：数组反序）
void reverse(int a[], int n)
{
      int i; // 循环变量
      int temp; // 临时变量
      
      for(i = 0; i < n/2; i++) {
            temp = a[i];
            a[i] = a[n - 1 - i];
            a[n - 1 - i] = temp;
      }      
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
 

• 运行程序，查看结果
  

四、递推算法与递归算法

（一）递推算法

从已知向未知不断拓展的思想方式。

（二）递归算法

从未知向已知不断回归的思想方式。

（三）案例演示 - 计算阶乘

• 拿一个简单的数学问题——阶乘——来说明这两种不同的思想方式。

（1）采用递推方式来计算 n!
起点：1! = 1
2! = 1! * 2
3! =2! * 3
……
终点：n! = (n-1)! * n

（2）采用递归方式来计算 n!
起点：n! = (n-1)! * n
(n-1)! = (n-2)! * (n-1)
(n-2)! = (n-3)! * (n-2)
……
终点： 1! = 1

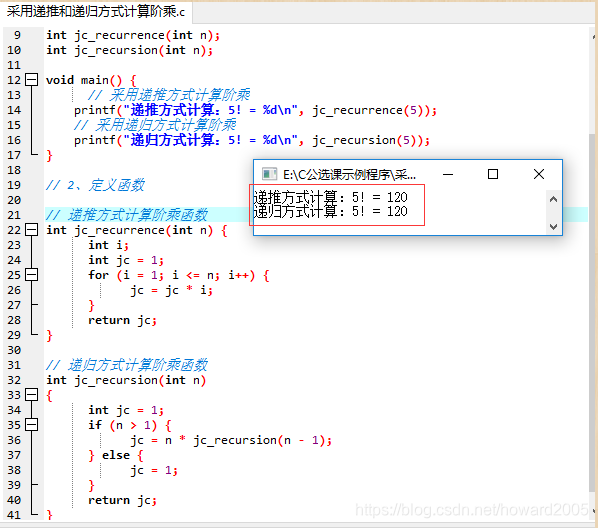
• 编写程序 - 采用递推和递归方式计算阶乘.c

/* 
  功能：采用递推和递归方式计算阶乘
  作者：华卫
  日期：2014年5月13日        
*/
#include "stdio.h"

// 1、声明函数
int jc_recurrence(int n); 
int jc_recursion(int n); 

void main() {
      // 采用递推方式计算阶乘
    printf("递推方式计算：5! = %d\n", jc_recurrence(5));
    // 采用递归方式计算阶乘
    printf("递归方式计算：5! = %d\n", jc_recursion(5));
}

// 2、定义函数

// 递推方式计算阶乘函数
int jc_recurrence(int n) {
      int i;
      int jc = 1;
      for (i = 1; i <= n; i++) {
            jc = jc * i;
      }
      return jc;
}

// 递归方式计算阶乘函数
int jc_recursion(int n)
{
      int jc = 1;
      if (n > 1) {
            jc = n * jc_recursion(n - 1);
      } else {
            jc = 1;
      }
      return jc;
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
 

• 运行程序，查看结果
  

文章来源: howard2005.blog.csdn.net，作者：howard2005，版权归原作者所有，如需转载，请联系作者。

原文链接：howard2005.blog.csdn.net/article/details/112576464