目录

一，幂和

二，多边形数

三，OJ实战

51Nod - 2172 ProjectEuler 6

一，幂和

幂和

其中最常见的是，   

那么，有没有求取高阶幂和的通用方法呢？

通用方法有很多，这里介绍高中数学常用的数列技巧的方法：

两边累积求和得到 

如k=3，

即

所以

二，多边形数

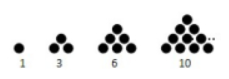
三角形数

四边形数

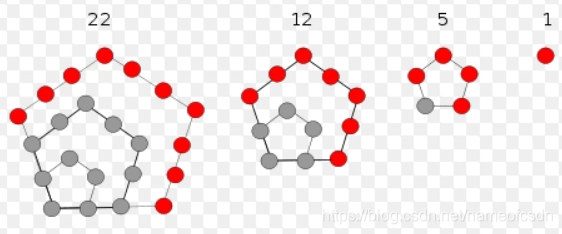
五边形数

六边形数

一般的，

不难发现， 即六边形数都是三角形数

三，OJ实战

51Nod - 2172 ProjectEuler 6

前10个正整数的平方和是
 1^2+2^2+⋯+10^2=385

前10个正整数和的平方是
 (1+2+⋯+10)^2=3025

和的平方减去平方和是3025 - 385 = 2640。

输入n，求前n个正整数和的平方 减去 平方和。

Input

输入第一行组数T， 接下来T行，每行一个整数n。 (1 <= T <= 100) (1 <= n <= 300)

Output

对于每组数据，输出一个数，表示和的平方减去平方和。

Sample Input

  

   

    

     

    
    

     

      3
     
    
   

    

     

    
    

     

      3
     
    
   

    

     

    
    

     

      10
     
    
   

    

     

    
    

     

      100
     
    
  
 

Sample Output

  

   

    

     

    
    

     

      22
     
    
   

    

     

    
    

     

      2640
     
    
   

    

     

    
    

     

      25164150
     
    
  
 

  

   

    

     

    
    

     

      #include<iostream>
     
    
   

    

     

    
    

     

      using namespace std;
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      int main()
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
    long long t,n;
     
    
   

    

     

    
    

     

          cin>>t;
     
    
   

    

     

    
    

     
    while(t--){
     
    
   

    

     

    
    

     

              cin>>n;
     
    
   

    

     

    
    

     

              cout<<n*(3*n+2)*(n*n-1)/12<<endl;
     
    
   

    

     

    
    

     

          }
     
    
   

    

     

    
    

     
    return 0;
     
    
   

    

     

    
    

     

      }
     
    
  
 

文章来源: blog.csdn.net，作者：csuzhucong，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/nameofcsdn/article/details/116992158