- 微信
- 微博
  
  分享文章到微博
- 复制链接
  
  复制链接到剪贴板

欧拉Gamma函数、Beta函数、余元公式

用户已注销发表于 2021/11/19 02:59:06 2021/11/19

【摘要】目录一，欧拉Gamma函数 1，Gamma函数 2，高斯形式 3，sin πx 4，其他形式二，余元公式 1，余元公式 2，应用三，欧拉Beta函数 1，Beta函数 2，和Gamma函数的关系 3，Beta函数的性质四，Gamma函数的导数 1，拆分 2，可导 3，Gamma函数的导数 4，G...

一，欧拉Gamma函数

1，Gamma函数

$Gamma(x)=int_{0}^{+infty} e^{-t} t^{x-1} d t$

2，高斯形式

$Gamma(x)=lim _{n rightarrow+infty} frac{n !}{x(x+1) cdots cdot(x+n)} cdot n^{x}$

证明：

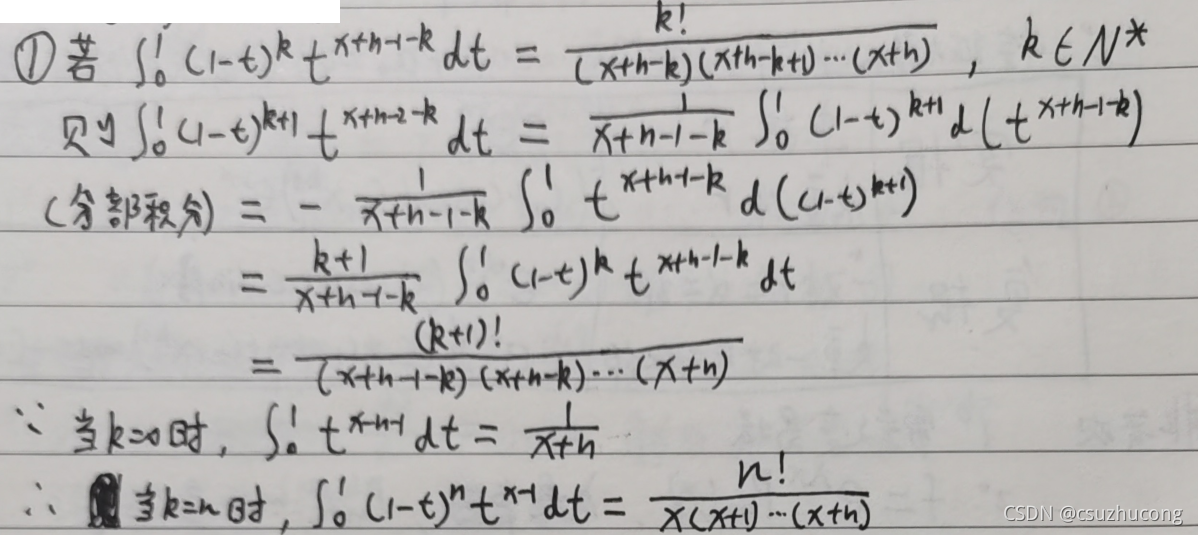
3，sin πx

$sin pi x=pi x lim _{n rightarrow+infty} prod ^n_{k=1}left(1-frac{x^{2}}{k^{2}}right)$

证明：

4，其他形式

（1）

$Gamma(x)=int_{0}^{+infty} e^{-t} t^{x-1} d t$

（2）

二，余元公式

1，余元公式

$Gamma(x) Gamma(1-x)=frac{pi}{sin pi x}$

证明：

$Gamma (x) Gamma (1-x) =lim_{n rightarrow+infty} frac{n ! cdot n^{x} cdot n ! cdot n^{1-x}}{x(x+1) cdots(x+n) (1-x)(2-x) cdots(n+1-x)}$

$=frac{1}{xlim _{nrightarrow+infty} left(frac{1-x^{2}}{1^{2}} cdot frac{2^2-x^{2}}{2^{2}} cdots ldots frac{n^{2}-x^{2}}{n^{2}}right)}=frac{pi}{sin pi x}$

2，应用

（1） $Gamma(frac{1}{2})=sqrt pi$

即 $int_{0}^{+infty} e^{-t} t^{-1/2} d t=sqrtpi$

（2）上式中，令，则

$int_0^{+infty}e^{-u^2}du=frac{sqrtpi}{2}$

（3） $Gamma(n+frac{1}{2})=frac{(2n-1)!!sqrtpi}{2^n}$

三，欧拉Beta函数

1，Beta函数

$B(x, y)=int_{0}^{1} t^{x-1}(1-t)^{y-1} d t, quad x>0, y>0$

2，和Gamma函数的关系

$B(x,y)=frac{Gamma (x)Gamma(y)}{Gamma(x+y)}$

证明：

（1）取，则

$B(x, y)=2 int_{0}^{frac{pi}{2}}(sin theta)^{2 x-1}(cos theta)^{2y-1} d theta$

（2） $Gamma(x) Gamma(y)=int_{0}^{+infty} e^{-u} u^{x- 1} d u int_{0}^{+infty} e^{-v} v^{y-1} d v$

设，则

$begin{aligned} Gamma(x) Gamma(y)&=int_{-infty}^{+infty} int_{-infty}^{+infty} e^{-left(alpha^{2}+b^{2}right)}|a|^{2 x-1}|b|^{2 y-1} d a d b, quad a=r cos theta, b=r sin theta\ &=int_{0}^{2 pi} int_{0}^{+infty} e^{-r^{2}}|r cos theta|^{2 x-1}|r sin theta|^{2y-1} r d r d theta\ &=int_{0}^{+infty} e^{-r^{2}} r^{2 x+2 y-1} d r int_{0}^{2 pi}|cos theta|^{2 x- 1}|sin theta|^{2 y-1} d theta\ &=frac{1}{2} Gamma(x+y) times 4 int_{0}^{frac{pi}{2}} cos ^{2 x-1} theta sin ^{2y-1} theta d theta\ &=Gamma(x+y) B(x, y) end{aligned}$

3，Beta函数的性质

四，Gamma函数的导数

1，拆分

$Gamma(x)=int_{0}^{+infty} e^{-t} t^{x-1} d t$ $=int_{0}^{1} e^{-t} t^{x-1} d t+int_{1}^{+infty} e^{-t} t^{x-1} d t$

其中 $int_{0}^{1} e^{-t} t^{x-1} d t$ 显然可导

2，可导

设 $f(x)=int_{1}^{+infty} e^{-t} t^{x-1} d t$ ，则f(x)严格递增

$begin{aligned} lim _{Delta x rightarrow 0} frac{f(x+Delta x)-f(x)}{Delta x}=&quad lim _{Delta x rightarrow 0} int_{1}^{+infty} e^{-t} t^{x-1} frac{t^{Delta x}-1}{Delta x} d t\ &=int_{1}^{+infty} e^{-t} t^{x-1} ln t d t end{aligned}$

$therefore f'(x)=int_{1}^{+infty} e^{-t} t^{x-1} ln t d t$

3，Gamma函数的导数

$Gamma'(x)=int_{0}^{+infty} e^{-t} t^{x-1} ln t d t$

$Gamma^{(n)}(x)=int_{0}^{+infty} e^{-t} t^{x-1} (ln t)^n d t$

4，Gamma函数在x=1处的导数

（1）

$Gamma'(1)=int_{0}^{+infty} e^{-t} ln t d t$

（2）

（3）

（4）

参考：欧拉常数

文章来源: blog.csdn.net，作者：csuzhucong，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/nameofcsdn/article/details/120597251

点赞
收藏
关注作者

0/1000

抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认取消

欧拉Gamma函数、Beta函数、余元公式

一，欧拉Gamma函数

1，Gamma函数

2，高斯形式

3，sin πx

4，其他形式

二，余元公式

1，余元公式

2，应用

三，欧拉Beta函数

1，Beta函数

2，和Gamma函数的关系

3，Beta函数的性质

四，Gamma函数的导数

1，拆分

2，可导

3，Gamma函数的导数

4，Gamma函数在x=1处的导数

全部回复

设置昵称

关于作者

目录

加入云驻计划，成为创作者

欧拉Gamma函数、Beta函数、余元公式

一，欧拉Gamma函数

1，Gamma函数

2，高斯形式

3，sin πx

4，其他形式

二，余元公式

1，余元公式

2，应用

三，欧拉Beta函数

1，Beta函数

2，和Gamma函数的关系

3，Beta函数的性质

四，Gamma函数的导数

1，拆分

2，可导

3，Gamma函数的导数

4，Gamma函数在x=1处的导数

全部回复

设置昵称

关于作者

目录

加入云驻计划，成为创作者

推荐阅读

相关产品