斯特林公式、沃利斯公式
【摘要】
目录
一,斯特林公式
1,公式
2,证明
3,更多项
4,变形
二,沃利斯公式
1,公式
2,变形
一,斯特林公式
1,公式
2,证明
3,更多项
用以上方法可以求出 的前任意多项。
4,变形
两边取对数
可用于计算机快速计算阶乘。 ...
目录
一,斯特林公式
1,公式

2,证明




3,更多项
用以上方法可以求出  的前任意多项。
的前任意多项。
4,变形

两边取对数

可用于计算机快速计算阶乘。
二,沃利斯公式
1,公式

证明:
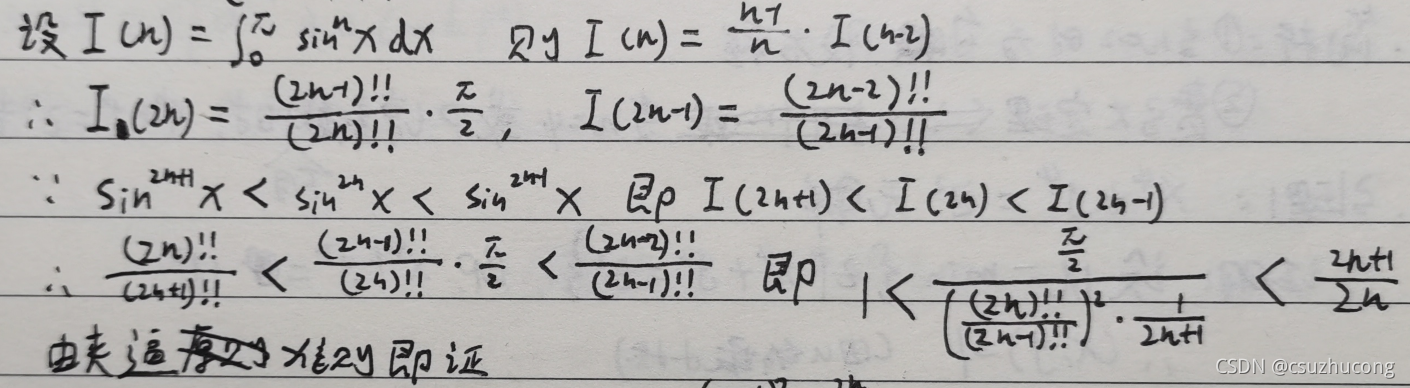
2,变形



参考 欧拉Gamma函数
文章来源: blog.csdn.net,作者:csuzhucong,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/nameofcsdn/article/details/120687924
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)