最小生成树
目录
一,Kruskal
算法思路:
开始把每个点当做一棵独立的树,每次选所有不在一棵树上的两点构成的边中的最短边,把这两点连起来,两棵树合并成一棵树,
每次连一条边,直到所有的点都连成一棵树。
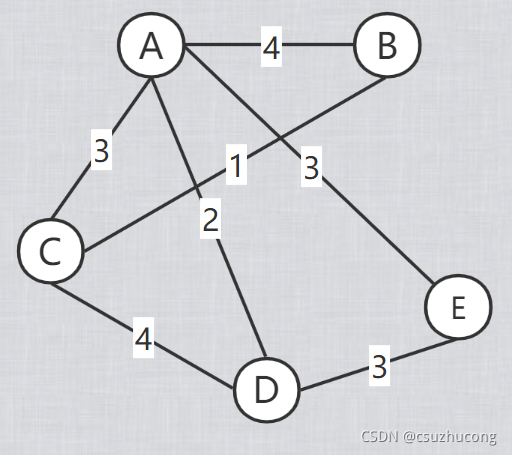
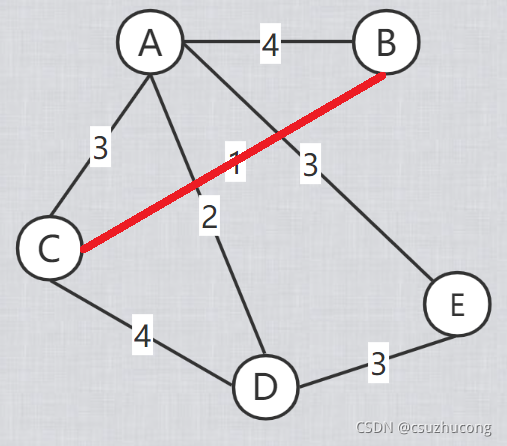
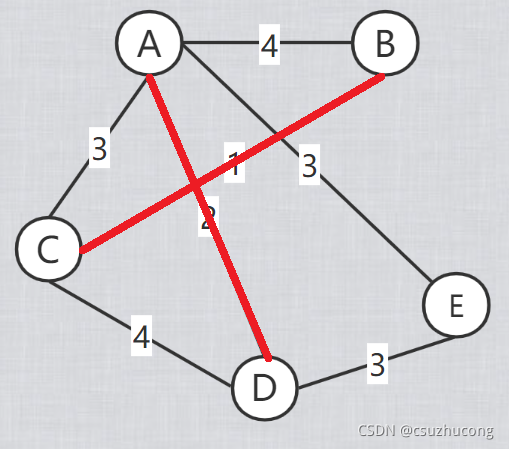
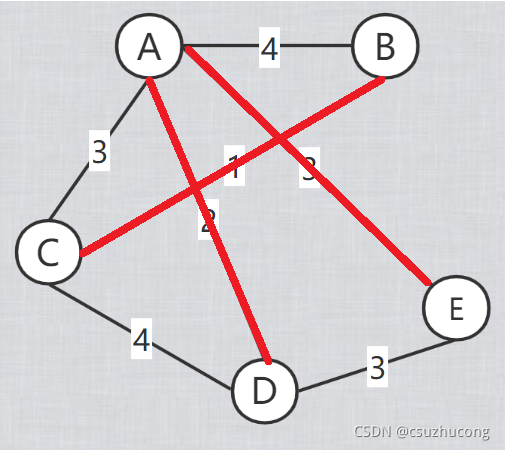

模板代码:
-
const int N = 1000; //点的最大数量
-
int en; //点的数量
-
// TODO 用数组或者vector记录点的信息,id要从0开始
-
-
int fa[N];
-
int find(int x) //找祖先
-
{
-
if (fa[x] == x)return x;
-
return fa[x] = find(fa[x]);
-
}
-
void merge(int i, int j)
-
{
-
fa[find(i)] = j;
-
}
-
bool inSameSet(int i, int j)
-
{
-
return find(i) == find(j);
-
}
-
-
struct Edge
-
{
-
int a;//端点id
-
int b;//端点id
-
int dist;
-
};
-
-
bool cmp(Edge a, Edge b)
-
{
-
return a.dist < b.dist;
-
}
-
-
int getLen(int i, int j) // 计算id为i和j的2个点的距离
-
{
-
return 0; // TODO 根据实际情况修改
-
}
-
vector<Edge> getEdge() // 获取所有的边
-
{
-
// TODO 根据实际情况修改
-
vector<Edge> v;
-
for (int i = 0; i < en; i++)for (int j = i + 1; j < en; j++) {
-
Edge e = { i,j,getLen(i,j) };
-
v.push_back(e);
-
}
-
return v;
-
}
-
-
//计算最小生成树,结果按照边从小到大排序
-
vector<pair<int, int>> minCostConnectPoints()
-
{
-
vector<Edge> v = getEdge();
-
sort(v.begin(), v.end(), cmp);
-
for (int i = 0; i < en; i++)fa[i] = i;
-
vector<pair<int, int>>ans;
-
for (int i = 0, j = 0; j < en - 1; i++)
-
{
-
if (inSameSet(v[i].a, v[i].b))continue;
-
merge(v[i].a, v[i].b);
-
ans.push_back(make_pair(v[i].a, v[i].b));
-
j++;
-
}
-
return ans;
-
}
时间复杂度:O(ElogE),其中E是边的数量。
二,Kruskal实战
POJ 2349 Arctic Network
题目:
Description
The Department of National Defence (DND) wishes to connect several northern outposts by a wireless network. Two different communication technologies are to be used in establishing the network: every outpost will have a radio transceiver and some outposts will in addition have a satellite channel.
Any two outposts with a satellite channel can communicate via the satellite, regardless of their location. Otherwise, two outposts can communicate by radio only if the distance between them does not exceed D, which depends of the power of the transceivers. Higher power yields higher D but costs more. Due to purchasing and maintenance considerations, the transceivers at the outposts must be identical; that is, the value of D is the same for every pair of outposts.
Your job is to determine the minimum D required for the transceivers. There must be at least one communication path (direct or indirect) between every pair of outposts.
Input
The first line of input contains N, the number of test cases. The first line of each test case contains 1 <= S <= 100, the number of satellite channels, and S < P <= 500, the number of outposts. P lines follow, giving the (x,y) coordinates of each outpost in km (coordinates are integers between 0 and 10,000).
Output
For each case, output should consist of a single line giving the minimum D required to connect the network. Output should be specified to 2 decimal points.
Sample Input
1
2 4
0 100
0 300
0 600
150 750
Sample Output
212.13
这个题目是说,有p个站点,其中有s个可以卫星相连。(卫星不是站点)
剩下还有p-s个站点,所以还需要用p-s条直线段把这p个站点全部连接起来。
求最长的直线段至少有多长。
比如本题,我们选0,300和0,600连接卫星,
0,100用200的线段可以连上0,300,150,750用150*sqrt(2)的线段可以连上0,600
所以答案是150*sqrt(2)=212.13
所以说,这个题目的意思就是,给你p个点的坐标,所有的点都是相连的,
选1个生成树,较大的s-1条边可以用卫星代替,较小的p-s条边中,最长的那个,至少有多长?
这个题目很明显就是克鲁斯卡尔(Kruskal)算法了。
代码:
-
#include<iostream>
-
#include<vector>
-
#include<stdio.h>
-
#include<algorithm>
-
#include<iomanip>
-
#include<cmath>
-
using namespace std;
-
-
const int N = 500; //点的最大数量
-
int en; //点的数量
-
// 用数组或者vector记录点的信息,id要从0开始
-
struct node
-
{
-
int x;
-
int y;
-
};
-
node nod[N];
-
-
int fa[N];
-
int find(int x) //找祖先
-
{
-
if (fa[x] == x)return x;
-
return fa[x] = find(fa[x]);
-
}
-
void merge(int i, int j)
-
{
-
fa[find(i)] = j;
-
}
-
bool inSameSet(int i, int j)
-
{
-
return find(i) == find(j);
-
}
-
-
struct Edge
-
{
-
int a;//端点id
-
int b;//端点id
-
int dist;
-
};
-
-
bool cmp(Edge a, Edge b)
-
{
-
return a.dist < b.dist;
-
}
-
-
int getLen(int i, int j) // 计算id为i和j的2个点的距离
-
{
-
return (nod[j].x - nod[i].x) * (nod[j].x - nod[i].x)
-
+ (nod[j].y - nod[i].y) * (nod[j].y - nod[i].y);
-
}
-
vector<Edge> getEdge() // 获取所有的边
-
{
-
// TODO 根据实际情况修改
-
vector<Edge> v;
-
for (int i = 0; i < en; i++)for (int j = i + 1; j < en; j++) {
-
Edge e = { i,j,getLen(i,j) };
-
v.push_back(e);
-
}
-
return v;
-
}
-
-
//计算最小生成树,结果按照边从小到大排序
-
vector<pair<int, int>> minCostConnectPoints()
-
{
-
vector<Edge> v = getEdge();
-
sort(v.begin(), v.end(), cmp);
-
for (int i = 0; i < en; i++)fa[i] = i;
-
vector<pair<int, int>>ans;
-
for (int i = 0, j = 0; j < en - 1; i++)
-
{
-
if (inSameSet(v[i].a, v[i].b))continue;
-
merge(v[i].a, v[i].b);
-
ans.push_back(make_pair(v[i].a, v[i].b));
-
j++;
-
}
-
return ans;
-
}
-
-
int main()
-
{
-
int t, s;
-
cin >> t;
-
for (int i = 0; i < t; i++)
-
{
-
cin >> s >> en;
-
for (int j = 0; j < en; j++)
-
{
-
cin >> nod[j].x >> nod[j].y;
-
}
-
vector<pair<int, int>> v = minCostConnectPoints();
-
pair<int, int> pa = v[en - s - 1];
-
double c = 1.0;
-
cout << fixed << setprecision(2) << sqrt(c * getLen(pa.first, pa.second)) << endl;
-
}
-
return 0;
-
}
力扣 1584. 连接所有点的最小费用
给你一个points 数组,表示 2D 平面上的一些点,其中 points[i] = [xi, yi] 。
连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 :|xi - xj| + |yi - yj| ,其中 |val| 表示 val 的绝对值。
请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时,才认为所有点都已连接。
示例 1:
输入:points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出:20
解释:
我们可以按照上图所示连接所有点得到最小总费用,总费用为 20 。
注意到任意两个点之间只有唯一一条路径互相到达。
示例 2:
输入:points = [[3,12],[-2,5],[-4,1]]
输出:18
示例 3:
输入:points = [[0,0],[1,1],[1,0],[-1,1]]
输出:4
示例 4:
输入:points = [[-1000000,-1000000],[1000000,1000000]]
输出:4000000
示例 5:
输入:points = [[0,0]]
输出:0
提示:
1 <= points.length <= 1000
-106 <= xi, yi <= 106
所有点 (xi, yi) 两两不同。
-
const int N = 1000; //点的最大数量
-
int en; //点的数量
-
// TODO 用数组或者vector记录点的信息,id要从0开始
-
vector<vector<int>>p;
-
-
int fa[N];
-
int find(int x) //找祖先
-
{
-
if (fa[x] == x)return x;
-
return fa[x] = find(fa[x]);
-
}
-
void merge(int i, int j)
-
{
-
fa[find(i)] = j;
-
}
-
bool inSameSet(int i, int j)
-
{
-
return find(i) == find(j);
-
}
-
-
struct Edge
-
{
-
int a;//端点id
-
int b;//端点id
-
int dist;
-
};
-
-
bool cmp(Edge a, Edge b)
-
{
-
return a.dist < b.dist;
-
}
-
-
int getLen(int i, int j) // 计算id为i和j的2个点的距离
-
{
-
return abs(p[i][0] - p[j][0]) + abs(p[i][1] - p[j][1]);
-
}
-
vector<Edge> getEdge() // 获取所有的边
-
{
-
// TODO 根据实际情况修改
-
vector<Edge> v;
-
for (int i = 0; i < en; i++)for (int j = i + 1; j < en; j++) {
-
Edge e = { i,j,getLen(i,j) };
-
v.push_back(e);
-
}
-
return v;
-
}
-
-
//计算最小生成树,结果按照边从小到大排序
-
vector<pair<int, int>> minCostConnectPoints2()
-
{
-
vector<Edge> v = getEdge();
-
sort(v.begin(), v.end(), cmp);
-
for (int i = 0; i < en; i++)fa[i] = i;
-
vector<pair<int, int>>ans;
-
for (int i = 0, j = 0; j < en - 1; i++)
-
{
-
if (inSameSet(v[i].a, v[i].b))continue;
-
merge(v[i].a, v[i].b);
-
ans.push_back(make_pair(v[i].a, v[i].b));
-
j++;
-
}
-
return ans;
-
}
-
-
class Solution {
-
public:
-
int minCostConnectPoints(vector<vector<int>>& points) {
-
p = points;
-
en = p.size();
-
vector<pair<int, int>> v = minCostConnectPoints2();
-
int ans = 0;
-
for (pair<int, int> vi : v) {
-
ans += getLen(vi.first, vi.second);
-
}
-
return ans;
-
}
-
};
三,Prim
Prim和Dijkstra几乎一样,区别只在于Dijkstra的距离的每个点到起点的路径总长,而Prim的距离就是每个点到最近一个点的距离。


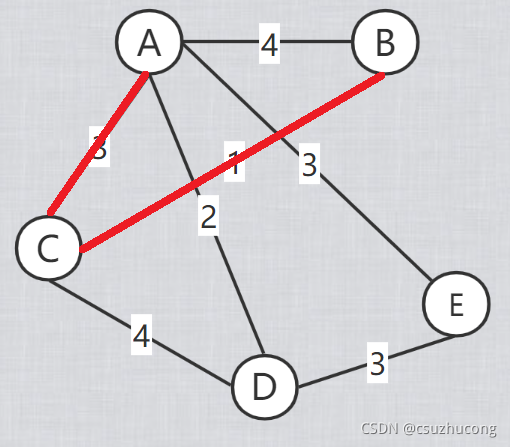
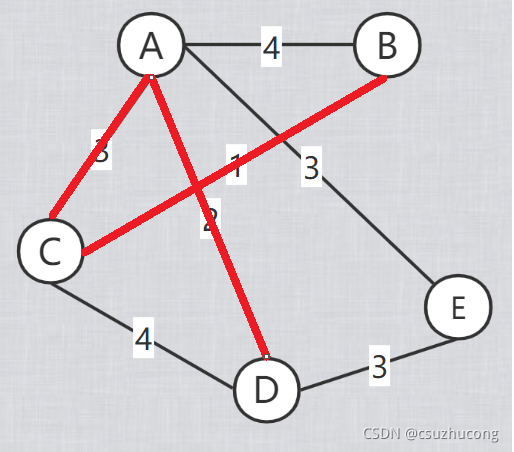
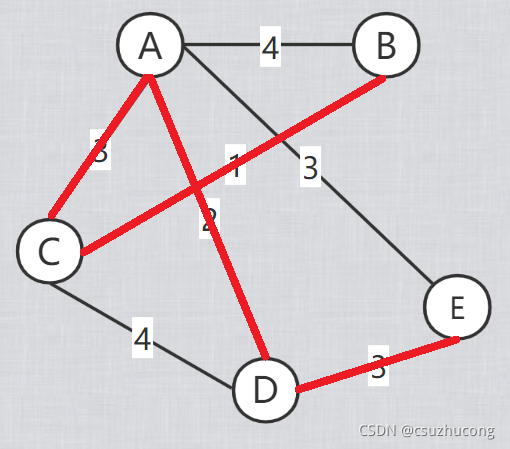
模板代码:
-
const int N = 1000; //点的最大数量
-
int en; //点的数量
-
// TODO 用数组或者vector记录点的信息,id要从0开始
-
vector<vector<int>>p;
-
bool visit_[N];
-
int minLen[N];
-
-
int getLen(int i, int j) // 计算id为i和j的2个点的距离
-
{
-
return 0; // TODO 根据实际情况修改
-
}
-
-
int getStartId()
-
{
-
int m = INT_MAX;
-
int ans = 0;
-
for (int i = 0; i < en; i++) {
-
for (int j = 0; j < en; j++) {
-
if (i != j && m > getLen(i, j)) {
-
m = getLen(i, j);
-
ans = i;
-
}
-
}
-
}
-
return ans;
-
}
-
void init()
-
{
-
for (int i = 0; i < en; i++) {
-
minLen[i] = INT_MAX;
-
visit_[i] = false;
-
}
-
minLen[getStartId()] = INT_MIN;
-
}
-
-
int getId()
-
{
-
int m= INT_MAX;
-
int ans = 0;
-
for (int i = 0; i < en; i++) {
-
if (!visit_[i] && m > minLen[i]) {
-
m = minLen[i];
-
ans = i;
-
}
-
}
-
return ans;
-
}
-
void fresh(int id)
-
{
-
for (int i = 0; i < en; i++) {
-
if (!visit_[i])minLen[i] = min(minLen[i], getLen(i, id));
-
}
-
}
-
-
//计算最小生成树,结果按照边从小到大排序
-
vector<pair<int, int>> minCostConnectPoints()
-
{
-
init();
-
vector<pair<int, int>>ans;
-
for (int i = 0; i < en; i++) {
-
int id = getId();
-
for (int j = 0; j < en; j++) {
-
if (visit_[j] && getLen(id, j) == minLen[id]) {
-
ans.push_back(make_pair(id, j));
-
break;
-
}
-
}
-
visit_[id] = true;
-
fresh(id);
-
}
-
return ans;
-
}
时间复杂度:O(V^2),其中V是点的数量。
四,Prim实战
力扣 1584. 连接所有点的最小费用
题目同上
-
const int N = 1000; //点的最大数量
-
int en; //点的数量
-
// TODO 用数组或者vector记录点的信息,id要从0开始
-
vector<vector<int>>p;
-
bool visit_[N];
-
int minLen[N];
-
-
int getLen(int i, int j) // 计算id为i和j的2个点的距离
-
{
-
return abs(p[i][0] - p[j][0]) + abs(p[i][1] - p[j][1]);
-
}
-
-
int getStartId()
-
{
-
int m = INT_MAX;
-
int ans = 0;
-
for (int i = 0; i < en; i++) {
-
for (int j = 0; j < en; j++) {
-
if (i != j && m > getLen(i, j)) {
-
m = getLen(i, j);
-
ans = i;
-
}
-
}
-
}
-
return ans;
-
}
-
void init()
-
{
-
for (int i = 0; i < en; i++) {
-
minLen[i] = INT_MAX;
-
visit_[i] = false;
-
}
-
minLen[getStartId()] = INT_MIN;
-
}
-
-
int getId()
-
{
-
int m= INT_MAX;
-
int ans = 0;
-
for (int i = 0; i < en; i++) {
-
if (!visit_[i] && m > minLen[i]) {
-
m = minLen[i];
-
ans = i;
-
}
-
}
-
return ans;
-
}
-
void fresh(int id)
-
{
-
for (int i = 0; i < en; i++) {
-
if (!visit_[i])minLen[i] = min(minLen[i], getLen(i, id));
-
}
-
}
-
-
//计算最小生成树,结果按照边从小到大排序
-
vector<pair<int, int>> minCostConnectPoints2()
-
{
-
init();
-
vector<pair<int, int>>ans;
-
for (int i = 0; i < en; i++) {
-
int id = getId();
-
for (int j = 0; j < en; j++) {
-
if (visit_[j] && getLen(id, j) == minLen[id]) {
-
ans.push_back(make_pair(id, j));
-
break;
-
}
-
}
-
visit_[id] = true;
-
fresh(id);
-
}
-
return ans;
-
}
-
-
class Solution {
-
public:
-
int minCostConnectPoints(vector<vector<int>>& points) {
-
p = points;
-
en = p.size();
-
vector<pair<int, int>> v = minCostConnectPoints2();
-
int ans = 0;
-
for (pair<int, int> vi : v) {
-
ans += getLen(vi.first, vi.second);
-
}
-
return ans;
-
}
-
};
文章来源: blog.csdn.net,作者:csuzhucong,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/nameofcsdn/article/details/121004649
- 点赞
- 收藏
- 关注作者


评论(0)