【C/C++练习题】斐波那契数列

《剑指Offer》面试题10

1 问题

题目：写一个函数，输入n，求斐波那契（Fibonacci）数列的第n项。

2 分析

对于斐波那契数列问题，至少有递归和循环两种算法。下面就解法的角度，分析一下两种方法的优劣

递归：优点是思路简单，代码也比较直观；缺点是效率低，调用栈区空间会对时间和空间造成消耗（严重的话会造成栈溢出），另外在递归的过程中还可能有很多计算是重复的。

循环：提高的算法在时间上的效率。相对于递归实现，是比较实用的方法。

3 代码

  

   

    

     

    
    

     

      #include "iostream"
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      using namespace std;
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      //方式一：使用递归实现
     
    
   

    

     

    
    

     

      //输入：n
     
    
   

    

     

    
    

     

      //返回：结果值
     
    
   

    

     

    
    

     

      long long Fibonacci_Solution1(unsigned int n)
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	if (n == 0)
     
    
   

    

     

    
    

     

      	{
     
    
   

    

     

    
    

     
		return 0;
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     
	if (n == 1)
     
    
   

    

     

    
    

     

      	{
     
    
   

    

     

    
    

     
		return 1;
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
	return Fibonacci_Solution1(n-1) + Fibonacci_Solution1(n-2);
     
    
   

    

     

    
    

     

      }
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      //方式二：使用循环实现
     
    
   

    

     

    
    

     

      //输入：n
     
    
   

    

     

    
    

     

      //返回：结果值
     
    
   

    

     

    
    

     

      long long Fibonacci_Solution2(unsigned n)
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	int res[] = {0, 1};
     
    
   

    

     

    
    

     
	if (n <= 1)
     
    
   

    

     

    
    

     

      	{
     
    
   

    

     

    
    

     
		return res[n];
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
	long long FibNMinusOne = 0;
     
    
   

    

     

    
    

     
	long long FibNMinusTwo = 1;
     
    
   

    

     

    
    

     
	long long FibN = 0;
     
    
   

    

     

    
    

     
	for (int i = 2; i <= n; i++)
     
    
   

    

     

    
    

     

      	{
     
    
   

    

     

    
    

     

      		FibN = FibNMinusOne + FibNMinusTwo;
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      		FibNMinusOne = FibNMinusTwo;
     
    
   

    

     

    
    

     

      		FibNMinusTwo = FibN;
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     
	return FibN;
     
    
   

    

     

    
    

     

      }
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      //测试1
     
    
   

    

     

    
    

     

      void test01()
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	long long res = Fibonacci_Solution1(100);
     
    
   

    

     

    
    

     

      	cout << "res:" << res << endl;
     
    
   

    

     

    
    

     

      }
     
    
   

    

     

    
    

     

      //测试2
     
    
   

    

     

    
    

     

      void test02()
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	long long res = Fibonacci_Solution2(100);
     
    
   

    

     

    
    

     

      	cout << "res:" << res << endl;
     
    
   

    

     

    
    

     

      }
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      int main(int argc, char const *argv[])
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	if (argc >= 2)
     
    
   

    

     

    
    

     

      	{
     
    
   

    

     

    
    

     
		if ('1' == argv[1][0]) test01();
     
    
   

    

     

    
    

     
		if ('2' == argv[1][0]) test02();
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     
	else
     
    
   

    

     

    
    

     

      	{
     
    
   

    

     

    
    

     

      		cout << "please input an arg" << endl;
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     
	
     
    
   

    

     

    
    

     
	return 0;
     
    
   

    

     

    
    

     

      }
     
    
  
 

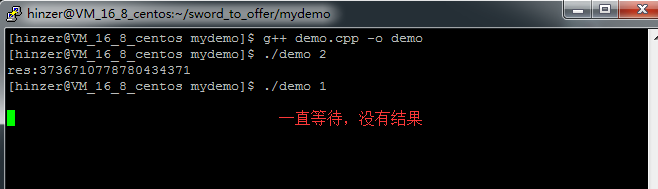
4 运行

使用递归方法，我等待了很长时间，也没等到一个结果（捂脸）。

5 同类型题

青蛙跳台阶问题

一只青蛙可以一次跳1层台阶，也可以一次跳2层台阶，问青蛙跳上n层台阶有多少种跳法？

• 当n等于0的时候，0层台阶，f(0)=0；
• 当n等于1的时候，1层台阶，也就1种跳法，f(1)=1;
• 当n等于2的时候，2层台阶，可以一次跳两层，也可以一层一层跳，两种跳法，f(2)=2；
• 当n层台阶时，如果第一次跳一层，那么剩下的n-1台阶就有f(n-1)种跳法；如果第一次跳两次层，剩下n-2的台阶有f(n-2)种跳法。显然，这是斐波那契数列的一个应用。

文章来源: blog.csdn.net，作者：hinzer，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/feit2417/article/details/96854187