目录

一，范数

1，广义范数

2，狭义范数

3，范数不等式

二，常见范数

一，范数

1，广义范数

广义范数是满足下列性质的任意函数：

2，狭义范数

狭义范数用来衡量向量的大小。

3，范数不等式

m>p>0, 则

当且仅当xi中至多有1个不为0时，不等式取等号。

也就是说，范数是递减的。

二，常见范数

（0）L0范数，表示非0分量的个数，其实这个是不规范的，严格来说并不是范数。

（1）p=1时，L1范数是向量中各个元素绝对值之和，即曼哈顿距离。

（2）p=2时，L2范数被称为欧几里得范数，即欧几里得距离，常简化表示为 ∥x∥，略去了下标 2。

（3）平方L2范数，即L2范数的平方，对 x 中每个元素的导数只取决于对应的元素。

（4）L∞范数，表示向量中具有最大幅值的元素的绝对值。

（5）F范数，即矩阵的Frobenius 范数，本质上和向量的L2范数是一样的。

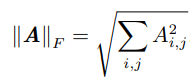
文章来源: blog.csdn.net，作者：csuzhucong，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/nameofcsdn/article/details/118499279