datawhale学习小组 Task4:方差分析
基本概念
方差分析(Analysis of variance, ANOVA) :——又称“变异数分析”
①用于两个及两个以上样本均数差别的显著性检验
②主要研究分类变量作为自变量时,对因变量的影响是否是显著
(1)组间因子 & 组内因子
组间因子:同一结果在同一变量的不同维度上单次试验
组内因子:同一结果在同一变量的不同维度上反复试验
(2)自变量 & 因变量
自变量:可以自由改变的量;因变量:随着自变量的改变而改变的量
简单点说,自变量是“原因”,而因变量就是“结果”
(3)均衡设计(balanced design) & 非均衡设计(unbalanced design)
研究组间变量时,设计的试验在每个组间因子下的观测数是否相等,相等就叫均衡设计(试验),否则,就叫非均衡设计(试验)
(4)主效应 & 交互效应
(5)单因素方差分析(one-way ANOVA)——单因素组间方差分析
(6)单因素组内方差分析——重复测量方差分析
(7)因素方差分析设计【双因素方差分析、三因素方差分析等】
(8)混合模型方差分析
(9)混淆因素(confounding factor)也被称作干扰变数(nuisance variable)
以焦虑症治疗为例,
现有两种治疗方案:认知行为疗法(CBT)和眼动脱敏再加工法(EMDR)。
招募10位焦虑症患者作为志愿者,
随机分配一半的人接受为期五周的CBT,另外一半接受为期五周的EMDR,
设计方案如表1-1所示。在治疗结束时,要求每位患者都填写状态特质焦虑问卷(STAI),也就是一份焦虑度测量的自我评测报告
表1-1 单因素组间方差分析
| CBT | EMDR |
|---|---|
| s1 | s6 |
| s2 | s7 |
| s3 | s8 |
| s4 | s9 |
| s5 | s10 |
治疗方案CBT和治疗方案EMDR是组间因子,因为每位患者都仅被分配到一个组别中,没有患者同时接受CBT和EMDR。表中字母s代表受试者(患者)。STAI是因变量,治疗方案是自变量(CBT、EMDR是治疗方案的不同维度)。由于在每种治疗方案下观测数相等,因此这种设计也称为均衡设计(balanced design);若观测数不同,则称作非均衡设计(unbalanced design)。
因为仅有一个类别型变量,表1的统计设计又称为单因素方差分析(one-way ANOVA),或进一步称为单因素组间方差分析。
方差分析主要通过F检验来进行效果评测,若治疗方案的F检验显著,则说明五周后两种疗法的STAI得分均值不同
方差分析基本步骤
研究分类型自变量对数值型因变量的影响
实际就是多个样本的均值比较
注意:数据必须是两列数值数据(分类型数值、度量值)
步骤:
F检验 原假设:三个品牌寿命方差没有显著差异
备择假设:三个品牌寿命方差有显著差异
注意:F检验结果中显著性>0.05才算方差齐
ANOVA检验结果
原假设:三个品牌电池寿命的均值相等(三个品牌电池寿命方差没有显著差异)
备择假设:三个品牌电池寿命的均值不全相等(三个品牌电池寿命方差有显著差异)
事后检验-----方差齐 LSD; 方差不齐 T2
事后多重比较是两两对比均值
4、 P<0.05,接受备择假设,两总体均值有显著性差异
P>0.05,接受原假设,两总体均值不存在显著性差异
案例—python实现
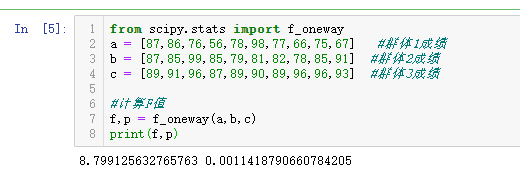
from scipy.stats import f_oneway
a = [87,86,76,56,78,98,77,66,75,67] #群体1成绩
b = [87,85,99,85,79,81,82,78,85,91] #群体2成绩
c = [89,91,96,87,89,90,89,96,96,93] #群体3成绩
#计算F值
f,p = f_oneway(a,b,c)
print(f,p)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
from scipy import stats
import pandas as pd
import numpy as np
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
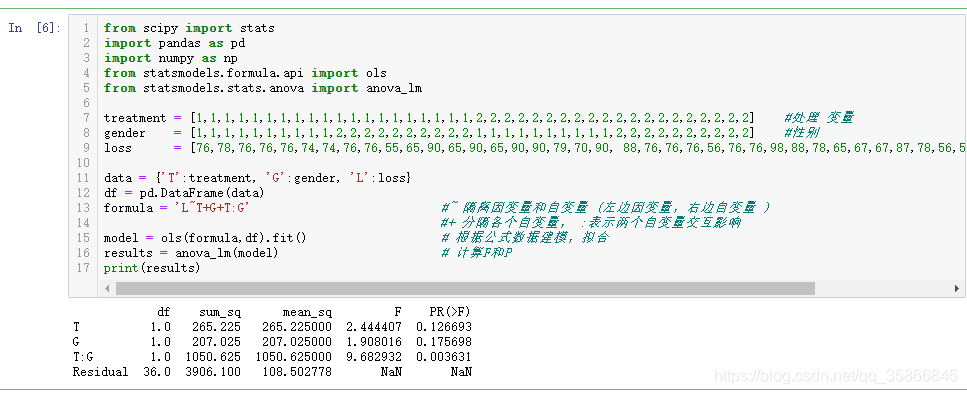
treatment = [1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2] #处理 变量
gender = [1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2] #性别
loss = [76,78,76,76,76,74,74,76,76,55,65,90,65,90,65,90,90,79,70,90, 88,76,76,76,56,76,76,98,88,78,65,67,67,87,78,56,54,56,54,56] #体重减少
data = {'T':treatment, 'G':gender, 'L':loss}
df = pd.DataFrame(data)
formula = 'L~T+G+T:G' #~ 隔离因变量和自变量 (左边因变量,右边自变量 )
#+ 分隔各个自变量, :表示两个自变量交互影响
model = ols(formula,df).fit() # 根据公式数据建模,拟合
results = anova_lm(model) # 计算F和P
print(results)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
import pandas as pd
import numpy as np
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
data = pd.DataFrame([[1, 1, 32],
[1, 2, 35],
[1, 3, 35.5],
[1, 4, 38.5],
[2, 1, 33.5],
[2, 2, 36.5],
[2, 3, 38],
[2, 4, 39.5],
[3, 1, 36],
[3, 2, 37.5],
[3, 3, 39.5],
[3, 4, 43]],
columns=['A', 'B', 'value'])
# 因素A的水平对结果的影响 'value ~ C(A)'
# 因素A和因素B的水平对结果的影响 'value ~ C(A) + C(B)'
# 因素A和因素B以及A和B的交互作用的水平对结果的影响 'value ~ C(A) + C(B) + C(A)*C(B)'
# 多因素无重复试验,不计算交互作用的影响
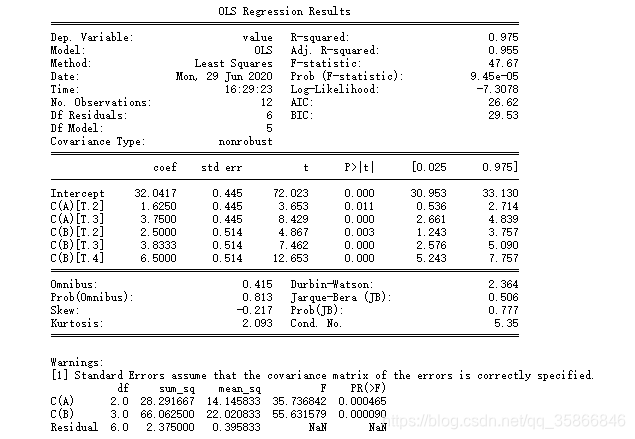
model = ols('value~C(A) + C(B)', data=data[['A', 'B', 'value']]).fit()
anovat = anova_lm(model)
print (model.summary())
print (anovat)
# #data为之前生成的DataFrame中选出的进行分析所需要的列,实际上ols是通过DataFrame的列名来获得试验结果和因素水平的数据的。最后用ols函数进行最小二乘线性拟合,用anova_lm函数进行方差分析并输出结果。
# # 如果是直接导入excel,通过pandas读取excel后,得到df,那么就不需要在ols()函数中data选择列,直接加入df
# model = ols('value~C(group) + C(time)',df).fit()
# anovat = anova_lm(model)
# print (model.summary())
# print (anovat)
# #进行单因素多方差分析,将formula中的C(B)去掉即可。
# #如果是对于有重复的多因素方差分析,将formula中加上C(A)*C(B)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
总结
方差分析的思想就是通过方差比较各族群之间有没有差异,
其中就是计算组内均方和和组间均方和,然后代入统计量做显著性检验
方差分析可以算是个线性模型,在统计学上面的检验原理和线性回归是差不多的
主要功能:
验证两组样本,或者两组以上的样本均值是否有显著性差异,即均值是否一样
注意:
①方差分析的原假设是:样本不存在显著性差异(即,均值完全相等);
②两样本数据无交互作用(即,样本数据独立)这一点在双因素方差分析中判断两因素是否独立时用。
原理:
SST=SS组间+SSR组内 (全部平方和=组间平方和+组内平方和)
说明:
方差分析本质上对总变异的解释。
组间平方和=每一组的均值减去样本均值
组内平方和=个体减去每组平方和
方差分析看的最终结果看的统计量是:F统计量、R2
参考资料:
datawhale组队学习——《率统计(四)-方差分析》
Task3:常见分布与假设检验
python中anova方差分析
文章来源: blog.csdn.net,作者:诡途,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/qq_35866846/article/details/107013315
- 点赞
- 收藏
- 关注作者


评论(0)