纯小白都能看懂的《单个神经元》、《随机梯度下降》、《逻辑与》
摘要
网上各种制造焦虑的软广《一文搞懂 / 学会 xxxx》
看的头大,但是这个专栏真的当的起一文搞懂神经网络
看完之后,就有种顿悟的感觉,我悟了
是我看过的把神经元讲的最清楚(没有之一)
虽然把链接放在文章开头会影响阅读,
但是我也不care了,强烈建议多遍阅读,先看大佬的文章
我这里,主要是相当于作为一篇笔记,或者读后感,
加深一下理解,并补充了部分自己的理解内容,做个记录
如果觉得有用,记得回来帮我点个赞
逻辑“与”介绍
高中数学知识:与(and)、或(or)、非(not) 、 异 或 \color{#BFBFBF}{、异或} 、异或
代码符号和关系解释
- 与 &:两个数都为1,结果才为1,否则为0
- 或 |:两个数中只要有一个为1,结果就为1,否则为0
- 非 !:数为0,结果为1,数为1,结果为0
- 异或 ^:两个数相同为0,不同为1
真命题与真命题,真命题;真命题与假命题,假命题;
真命题或真命题,真命题;真命题或假命题,真命题;
非真命题,假命题; 非假命题,真命题;
逻辑“与”的实验目标:
1&0 == 0 0&1 == 0
0&0 == 0 1&1 == 1
- 构建一个神经元根据上面四组数据自己学习到逻辑“与”规则
- 数据通项表示:x1&x2==y
数据整理
| x1 | x2 | y |
|---|---|---|
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
描点画图
将(x1,x2)视作一个坐标,将它描点在二维平面是这样的
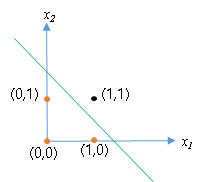
问题转换成为二分类即:
我们让神经元能够学习到将(0,1)、(0,0)、(1,0)这些点分类为0,将(1,1)这个点分类为1。
更直观的讲就是神经元得是像图中的这条直线一样,将四个点划分成两类。
在直线左下是分类为0,直线右上分裂为1.
高中数学加油站:
一条直线可以表示为 y = k x + b y=kx+b y=kx+b(此例 y = x 2 , x = x 1 y=x2,x=x1 y=x2,x=x1,可以写成 x 2 = k x 1 + b x2=kx1+b x2=kx1+b)
也可以写成 a x 1 + b x 2 + c = 0 ax1 + bx2 +c = 0 ax1+bx2+c=0
当斜率 < 0 <0 <0,
- 直线右边的所有点可以描述为 a x 1 + b x 2 + c > 0 ax1 + bx2 +c > 0 ax1+bx2+c>0,本例中表示当 x 1 x1 x1和 x 2 x2 x2都是1 ;
- 直线右边的所有点可以描述为 a x 1 + b x 2 + c < 0 ax1 + bx2 +c < 0 ax1+bx2+c<0,本例中表示当 x 1 x1 x1和 x 2 x2 x2至少有一个是0
约定俗成
在神经元里面大家喜欢把 x 1 x1 x1和 x 2 x2 x2前面的系数叫做权重(weight),把常数项叫做偏置(bias)。因此一般大家把 x x x前面系数命名为 ω \omega ω,把常数项命名为 b b b。
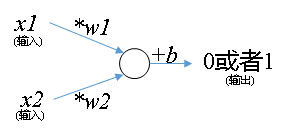
单个神经元
学计算机一个很重要的思维就是:任何一个系统都是由输入、输出、和处理组成。
什么叫神经元呢?
- 神经元在数学意义上就是一条直线(的函数表达式)
- 由输入、输出、和处理组成
- 有的地方说的感知机也是指的神经元

随机梯度下降
- 误差函数=代价函数=目标函数=损失函数,这四个词可以随意替换
- 误差函数(error)、代价函数(cost function)
- 目标函数(objective function)、损失函数(loss function)
- 误差函数是随 ω 1 、 ω 2 、 b \omega1、\omega2、b ω1、ω2、b的改变而改变。不同的参数 ω 1 、 ω 2 、 b \omega1、\omega2、b ω1、ω2、b对应不同的误差
神经元: f ( x 1 , x 2 ) = ω 1 ∗ x 1 + ω 2 ∗ x 2 + b f(x1,x2)=\omega1*x1+\omega2*x2+b f(x1,x2)=ω1∗x1+ω2∗x2+b ①
假设:
- 逻辑与(&)可以表示成一个函数 g ( x 1 , x 2 ) g(x1,x2) g(x1,x2)
- g ( 1 , 0 ) = 0 ; g ( 1 , 1 ) = 1 g(1,0)=0;g(1,1)=1 g(1,0)=0;g(1,1)=1等
g ( x 1 , x 2 ) g(x1,x2) g(x1,x2)为实际值, f ( x 1 , x 2 ) f(x1,x2) f(x1,x2)为预测值
真实值和测量值之间的误差可以两者相减并平方来量化
称为损失函数LOSS function,可以记为 L ( ω 1 、 ω 2 、 b ) L(\omega1、\omega2、b) L(ω1、ω2、b)
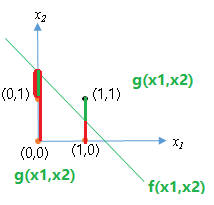
如图表示,红色 | 绿色 线段的长度,即实际值到预测线上对应预测值的距离
公式表示为
L ( ω 1 、 ω 2 、 b ) L(\omega1、\omega2、b) L(ω1、ω2、b)
= ( f ( x 1 , x 2 ) − g ( x 1 , x 2 ) ) 2 =(f(x1,x2)-g(x1,x2))^2 =(f(x1,x2)−g(x1,x2))2
= ( ω 1 ∗ x 1 + ω 2 ∗ x 2 + b − g ( x 1 , x 2 ) ) 2 =(\omega1*x1+\omega2*x2+b-g(x1,x2))^2 =(ω1∗x1+ω2∗x2+b−g(x1,x2))2
注意:对于给定的 x 1 , x 2 ; g ( x 1 , x 2 ) x1,x2;g(x1,x2) x1,x2;g(x1,x2)是个已知常量,且值域为{0,1};
即L是关于 ω 1 、 ω 2 、 b \omega1、\omega2、b ω1、ω2、b的三元一次函数
直观图就是类似于下图这样一口 “锅”
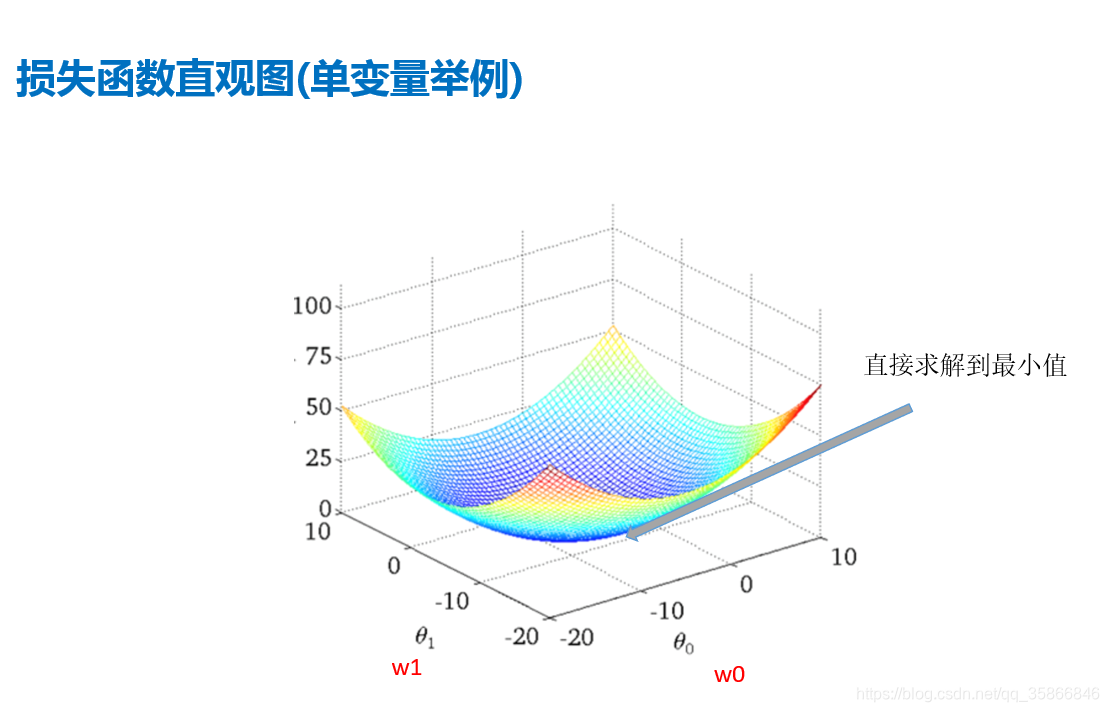
梯度下降三维图解
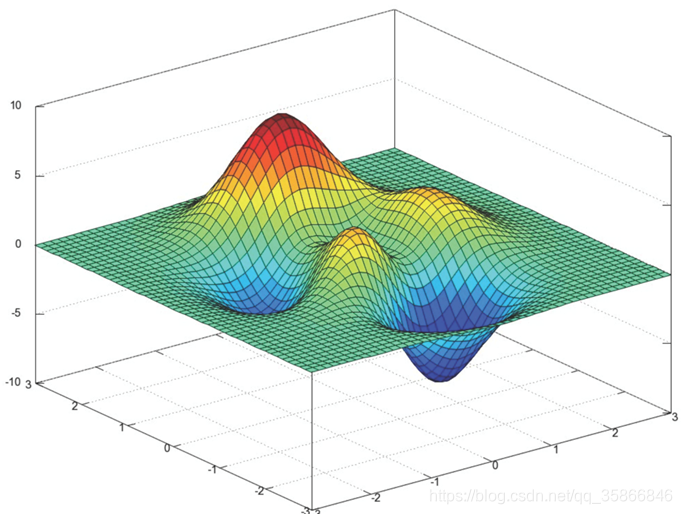
逻辑“与”代码实现
#面向对象的代码看不习惯,自己写了一遍函数定义的代码
import pandas as pd
"""
AND感知机实现
output =1 if weight1 * input1 + w2*input2 +bias >=0
output =0 if weight1 * input1 + w2*input2 +bias < 0
"""
#and为内置函数具有特殊意义,用and1表示
def and1():
# 1、定义权重和偏置项
weight1 = 0.8
weight2 = 1.2
bias = -1.3
# 2、定义输入和目标值(targets)
inputs = [(0, 0), (0, 1), (1, 0), (1, 1)]
targets = [False, False, False, True]
outputs = []
# 3、需要将输入和目标值 只用zip进行组合,然后一一遍历出来
for input, target in zip(inputs, targets):
# 4、做线性组合,并激活得到output(在3循环下面进行)
linear_combination = weight1 * input[0] + weight2 * input[1] + bias
# 阶跃函数激活
output = int(linear_combination > 0)
# 5、将输出output 追加到一个列表中(在3循环下面进行)
is_correct_string = "是" if output == target else "否"
# print(output, is_correct_string)
outputs.append([input[0], input[1], linear_combination, output, is_correct_string])
# 6、计算预测错误的个数-准确率
num_wrong = len([output[-1] for output in outputs if output[-1] == '否'])
# 7、可视化
output_frame = pd.DataFrame(
outputs, columns=['input1', 'input2', 'linear_combination', 'Activation output', 'is correct']
)
if not num_wrong:
print("恭喜你,全对了 \n")
else:
print('你错了 {} 个'.format(num_wrong))
print(output_frame.to_string(index=False))
# 复杂非线性分类 ——增加感知器 ——not感知机 增加了一层隐藏层
if __name__ == '__main__':
and1()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
文章来源: blog.csdn.net,作者:诡途,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/qq_35866846/article/details/107931710
- 点赞
- 收藏
- 关注作者


评论(0)