(建议收藏)matlab在线性代数问题中的计算机求解进阶问题及解决方案集锦
【摘要】
前言
关于MATLAB系列的精品专栏大家可参见
MATLAB-30天带你从入门到精通
MATLAB深入理解高级教程(附源码)
喜欢的小伙伴可自行订阅,你的支持就是我不断更新的动力哟!
线性代数问题的计算机求解进阶01
问题:
Jordan 矩阵是矩阵分析中一类很实用的矩阵,其一般形式为
试利用diag...
前言
关于MATLAB系列的精品专栏大家可参见
喜欢的小伙伴可自行订阅,你的支持就是我不断更新的动力哟!
线性代数问题的计算机求解进阶01
问题:
Jordan 矩阵是矩阵分析中一类很实用的矩阵,其一般形式为
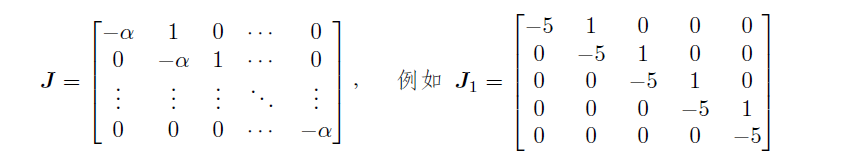
试利用diag() 函数给出构造J1 的语句。
解:
利用diag() 能够构造对角矩阵和次对角矩阵的性质,可以由下面语句建立起所需的矩阵。
>> J1=diag([-5 -5 -5 -5 -5])+diag([1 1 1 1],1)
J1 =
-5 1 0 0 0
0 -5 1 0 0
0 0 -5 1 0
0 0 0 -5 1
0 0 0 0 -5
拓展:
幂零矩阵是一类特殊的矩阵,其基本形
文章来源: wenyusuran.blog.csdn.net,作者:文宇肃然,版权归原作者所有,如需转载,请联系作者。
原文链接:wenyusuran.blog.csdn.net/article/details/117514315
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)