Matlab在线性代数中的应用（三）：求解非齐次线性方程组

前言

Matlab 中解非齐次线性方程组可以使用“\”。

虽然表面上只是一个简简单单的符号，而它的内部却包含许许多多的自适应算法，如对超定方程用最小二乘法，对欠定方程它将给出范数最小的一个解，解三对角阵方程组时用追赶法等。

另外，求解欠定方程组可以使用求矩阵 A 的行最简形命令 rref(A)，求出所有的基础解系。

01求超定方程组

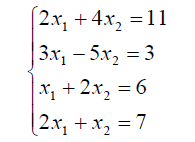
解：编写程序如下： 

a=[2,4;3,-5;1,2;2,1]; b=[11;3;6;7];

solution=a\b

求得最小二乘解为

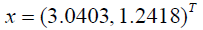
上面解超定方程组的“\”可以用伪逆命令 pinv 代替，且 pinv 的使用范围比“\”

更加广泛，pinv 也给出最小二乘解或最小范数解。

02用最小二乘解法解方程组

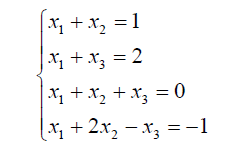
解：

编写程序如下： 

format rat

a=[1,1,0;1,0,1;1,1,1;1,2,-1];

文章来源: wenyusuran.blog.csdn.net，作者：文宇肃然，版权归原作者所有，如需转载，请联系作者。

原文链接：wenyusuran.blog.csdn.net/article/details/117524959