【大话数据结构C语言】42 图的深度优先遍历
【摘要】
欢迎关注我的公众号是【CodeAllen】,关注回复【1024】获取资源 程序员技术交流①群:736386324 ,程序员技术交流②群:371394777
还是类比学习,这里使用树来对比
树因为根结点只有一个,并且所有的结点都只有一个双亲,所以不是很难理...
欢迎关注我的公众号是【CodeAllen】,关注回复【1024】获取资源
程序员技术交流①群:736386324 ,程序员技术交流②群:371394777
还是类比学习,这里使用树来对比
树因为根结点只有一个,并且所有的结点都只有一个双亲,所以不是很难理解
但是图就比较复杂了,原因是图的任一顶点都可以和其余的所有顶点相邻接,因此极有可能存在重复走过某个顶点或漏了某个顶点的遍历过程
因此就引出了图的遍历方法,大佬们设计了两种遍历次序方案: 深度优先遍历和广度优先遍历
深度优化遍历(DepthFirstSearch),也有称为深度优化搜索,简称为DFS
它的具体思想类似于在家里找钥匙的方案,无论从哪一间房间开始都可以,将房间内的墙角、床头柜、床上、床下、衣柜、电视柜等挨个寻找,做到不放过任何一个死角,当所有的抽屉、储藏柜中全部都找遍,接着再寻找下一个房间
使用迷宫分析问题:
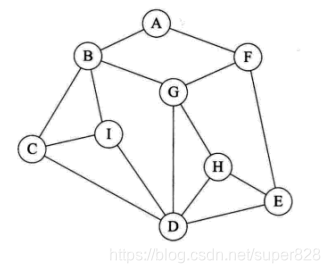
右手原则:
在没有碰到重复顶点的情况下, 分叉路口始终是向右手边走,每路过一个顶点就做一个记号右手原则:在没有碰到重复顶点的情况下,分叉路口始终是向右手边走,每路过一个顶点就做一个记号
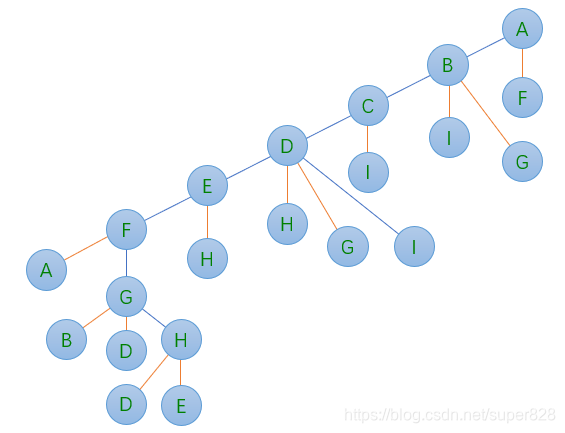
其实深度优先遍历就是一个递归的思想
你可能发现整个过程是一个树的遍历,下边是遍历的过程
代码实现:
AdList_DFS.c
-
#define TRUE 1
-
#define FALSE 0
-
#define MAX 256
-
-
typedef int Boolean; // 这里我们定义Boolean为布尔类型,其值为TRUE或FALSE
-
Boolean visited[MAX]; // 访问标志的数组
-
-
void DFS(GraphAdjList GL, int i)
-
{
-
EdgeNode *p;
-
-
visited[i] = TRUE;
-
printf("%c " GL->adjList[i].data);
-
p = GL->adjList[i].firstEdge;
-
-
while(p)
-
{
-
if( !visited[p->adjvex] )
-
{
-
DFS(GL, p->adjvex);
-
}
-
p = p->next;
-
}
-
}
-
-
// 邻接表的深度遍历操作
-
void DFSTraverse(GraphAdjList GL)
-
{
-
int i;
-
-
for( i=0; i < GL->numVertexes; i++ )
-
{
-
visited[i] = FALSE; // 初始化所有顶点状态都是未访问过状态
-
}
-
-
for( i=0; i < GL->numVertexes; i++ )
-
{
-
if( !visited[i] ) // 若是连通图,只会执行一次
-
{
-
DFS(GL, i);
-
}
-
}
-
}
AdMatrix_DFS.c
-
#define TRUE 1
-
#define FALSE 0
-
#define MAX 256
-
-
typedef int Boolean; // 这里我们定义Boolean为布尔类型,其值为TRUE或FALSE
-
Boolean visited[MAX]; // 访问标志的数组
-
-
void DFS(MGraph G, int i)
-
{
-
int j;
-
-
visited[j] = TRUE; // 访问过的顶点设置为TRUE
-
printf("%c ", G.vexs[i]); // 打印顶点
-
for( j=0; j < G.numVertexes; j++ )
-
{
-
if( G.arc[i][j]==1 && !visited[j] )
-
{
-
DFS(G, j); // 对为访问的邻接顶点递归调用
-
}
-
}
-
}
-
-
// 邻接矩阵的深度遍历操作
-
void DFSTraverse(MGraph G)
-
{
-
int i;
-
-
for( i=0; i < G.numVertexes; i++ )
-
{
-
visited[i] = FALSE; // 初始化所有顶点状态都是未访问过状态
-
}
-
-
for( i=0; i < G.numVertexes; i++ )
-
{
-
if( !visited[i] ) // 若是连通图,只会执行一次
-
{
-
DFS(G, i);
-
}
-
}
-
}
文章来源: allen5g.blog.csdn.net,作者:CodeAllen的博客,版权归原作者所有,如需转载,请联系作者。
原文链接:allen5g.blog.csdn.net/article/details/116549327
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)