【大话数据结构C语言】45 最小生成树(普里姆算法)
欢迎关注我的公众号是【CodeAllen】,关注回复【1024】获取资源
程序员技术交流①群:736386324 ,程序员技术交流②群:371394777
首先明确下概念,我们把构造连通网的最小代价生成树叫做最小生成树(Minimum Cost Spanning Tree)
给定一个连通网,求最小生成树的方法有:普里姆(Prim)算法 & 克鲁斯卡尔(Kruskal)算法
普里姆算法(Prim)
构建一个邻接矩阵
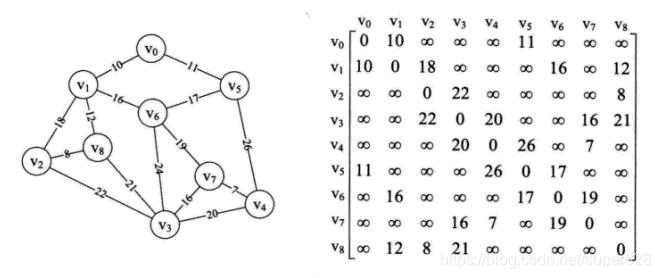
普里姆算法在找最小生成树时,将顶点分为两类,一类是在查找的过程中已经包含在树中的(假设为 A 类),剩下的是另一类(假设为 B 类)。
对于给定的连通网,起始状态全部顶点都归为 B 类。在找最小生成树时,选定任意一个顶点作为起始点,并将之从 B 类移至 A 类;然后找出 B 类中到 A 类中的顶点之间权值最小的顶点,将之从 B 类移至 A 类,如此重复,直到 B 类中没有顶点为止。所走过的顶点和边就是该连通图的最小生成树。
例如,通过普里姆算法查找图 2(a)的最小生成树的步骤为:
假如从顶点A出发,顶点 B、C、D 到顶点 A 的权值分别为 2、4、2,所以,对于顶点 A 来说,顶点 B 和顶点 D 到 A 的权值最小,假设先找到的顶点 B:
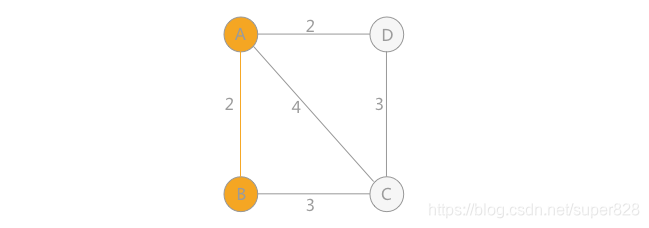
继续分析顶点 C 和 D,顶点 C 到 B 的权值为 3,到 A 的权值为 4;顶点 D 到 A 的权值为 2,到 B 的权值为无穷大(如果之间没有直接通路,设定权值为无穷大)。所以顶点 D 到 A 的权值最小:
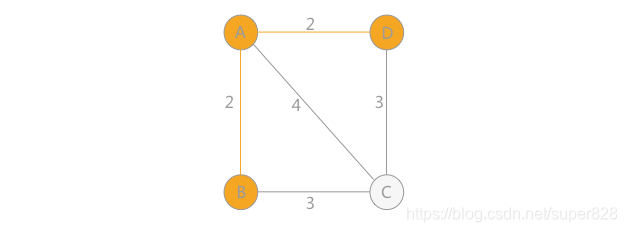
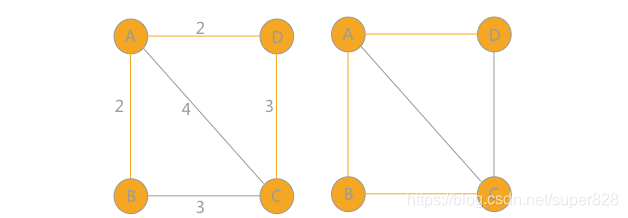
最后,只剩下顶点 C,到 A 的权值为 4,到 B 的权值和到 D 的权值一样大,为 3。所以该连通图有两个最小生成树:
prim.c
-
// Prim算法生成最小生成树
-
-
void MiniSpanTree_Prim(MGraph G)
-
-
{
-
-
int min, i, j, k;
-
-
int adjvex[MAXVEX]; // 保存相关顶点下标
-
-
int lowcost[MAXVEX]; // 保存相关顶点间边的权值
-
-
-
-
lowcost[0] = 0; // V0作为最小生成树的根开始遍历,权值为0
-
-
adjvex[0] = 0; // V0第一个加入
-
-
-
-
// 初始化操作
-
-
for( i=1; i < G.numVertexes; i++ )
-
-
{
-
-
lowcost[i] = G.arc[0][i]; // 将邻接矩阵第0行所有权值先加入数组
-
-
adjvex[i] = 0; // 初始化全部先为V0的下标
-
-
}
-
-
-
-
// 真正构造最小生成树的过程
-
-
for( i=1; i < G.numVertexes; i++ )
-
-
{
-
-
min = INFINITY; // 初始化最小权值为65535等不可能数值
-
-
j = 1;
-
-
k = 0;
-
-
-
-
// 遍历全部顶点
-
-
while( j < G.numVertexes )
-
-
{
-
-
// 找出lowcost数组已存储的最小权值
-
-
if( lowcost[j]!=0 && lowcost[j] < min )
-
-
{
-
-
min = lowcost[j];
-
-
k = j; // 将发现的最小权值的下标存入k,以待使用。
-
-
}
-
-
j++;
-
-
}
-
-
-
-
// 打印当前顶点边中权值最小的边
-
-
printf("(%d,%d)", adjvex[k], k);
-
-
lowcost[k] = 0; // 将当前顶点的权值设置为0,表示此顶点已经完成任务,进行下一个顶点的遍历
-
-
-
-
// 邻接矩阵k行逐个遍历全部顶点
-
-
for( j=1; j < G.numVertexes; j++ )
-
-
{
-
-
if( lowcost[j]!=0 && G.arc[k][j] < lowcost[j] )
-
-
{
-
-
lowcost[j] = G.arc[k][j];
-
-
adjvex[j] = k;
-
-
}
-
-
}
-
-
}
-
-
}
文章来源: allen5g.blog.csdn.net,作者:CodeAllen的博客,版权归原作者所有,如需转载,请联系作者。
原文链接:allen5g.blog.csdn.net/article/details/116618047
- 点赞
- 收藏
- 关注作者


评论(0)