【大话数据结构C语言】57 平衡二叉树(AVL树)
欢迎关注我的公众号是【CodeAllen】,关注回复【1024】获取精品学习资源
程序员技术交流①群:736386324 ,程序员技术交流②群:371394777
平衡二叉排序树
平衡二叉树是一种二叉排序树,其中每一个结点的左子树和右子树的高度差至多等于1
有两位俄罗斯数学家 G.M. Adelson-Velsky和E.M. Landis发明一种解决平衡二叉树的算法,所以很多资料称这样的平衡二叉树为AVL树
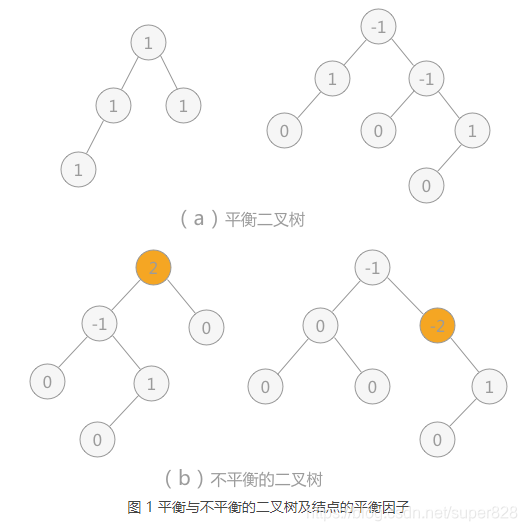
平衡因子:每个结点都有其各自的平衡因子,表示的就是其左子树深度同右子树深度的差。平衡二叉树中各结点平衡因子的取值只可能是:0、1 和 -1。
如图 1 所示,其中 (a) 的两棵二叉树中由于各个结点的平衡因子数的绝对值都不超过 1,所以 (a) 中两棵二叉树都是平衡二叉树;而 (b) 的两棵二叉树中有结点的平衡因子数的绝对值超过 1,所以都不是平衡二叉树。
二叉排序树转化为平衡二叉树
为了排除动态查找表中不同的数据排列方式对算法性能的影响,需要考虑在不会破坏二叉排序树本身结构的前提下,将二叉排序树转化为平衡二叉树。
例如,使用上一节的算法在对查找表{13,24,37,90,53}构建二叉排序树时,当插入 13 和 24 时,二叉排序树此时还是平衡二叉树:
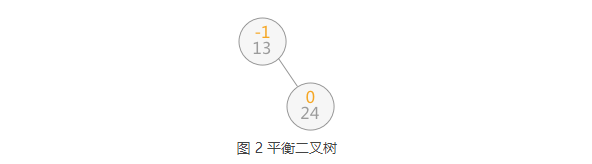
当继续插入 37 时,生成的二叉排序树如图 3(a),平衡二叉树的结构被破坏,此时只需要对二叉排序树做“旋转”操作(如图 3(b)),即整棵树以结点 24 为根结点,二叉排序树的结构没有破坏,同时将该树转化为了平衡二叉树:
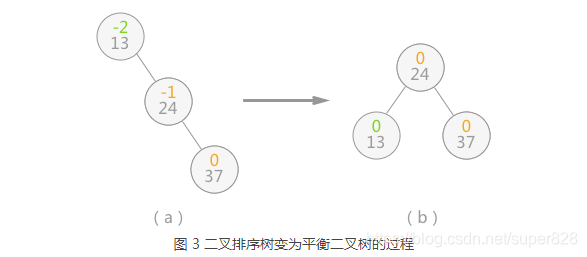
当二叉排序树的平衡性被打破时,就如同扁担的两头出现了一头重一头轻的现象,如图3(a)所示,此时只需要改变扁担的支撑点(树的树根),就能使其重新归为平衡。实际上图 3 中的 (b) 是对(a) 的二叉树做了一个向左逆时针旋转的操作。
继续插入 90 和 53 后,二叉排序树如图 4(a)所示,导致二叉树中结点 24 和 37 的平衡因子的绝对值大于 1 ,整棵树的平衡被打破。此时,需要做两步操作:
-
如图 4(b) 所示,将结点 53 和 90 整体向右顺时针旋转,使本该以 90 为根结点的子树改为以结点 53 为根结点;
-
如图 4(c) 所示,将以结点 37 为根结点的子树向左逆时针旋转,使本该以 37 为根结点的子树,改为以结点 53 为根结点;
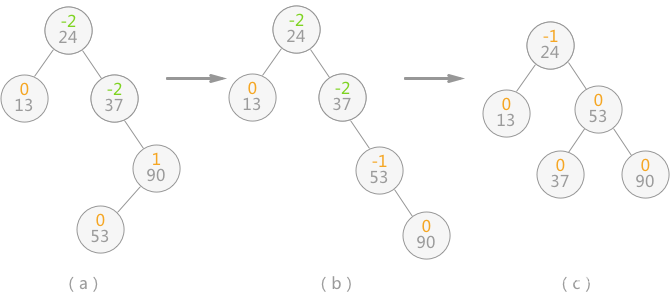
做完以上操作,即完成了由不平衡的二叉排序树转变为平衡二叉树。
当平衡二叉树由于新增数据元素导致整棵树的平衡遭到破坏时,就需要根据实际情况做出适当的调整,假设距离插入结点最近的“不平衡因子”为 a。则调整的规律可归纳为以下 4 种情况:
-
单向右旋平衡处理:若由于结点 a 的左子树为根结点的左子树上插入结点,导致结点 a 的平衡因子由 1 增至 2,致使以 a 为根结点的子树失去平衡,则只需进行一次向右的顺时针旋转,如下图这种情况:
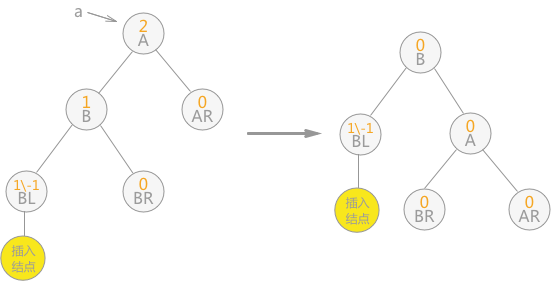
单向左旋平衡处理:如果由于结点 a 的右子树为根结点的右子树上插入结点,导致结点 a 的平衡因子由 -1变为 -2,则以 a 为根结点的子树需要进行一次向左的逆时针旋转,如下图这种情况:
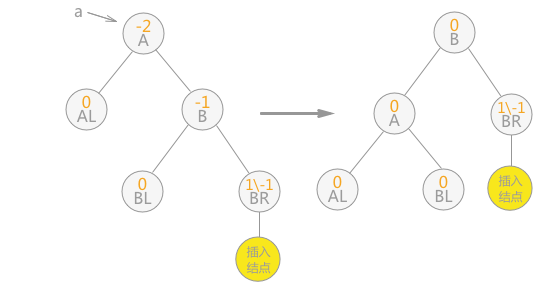
双向旋转(先左后右)平衡处理:如果由于结点 a 的左子树为根结点的右子树上插入结点,导致结点 a 平衡因子由 1 增至 2,致使以 a 为根结点的子树失去平衡,则需要进行两次旋转操作,如下图这种情况:
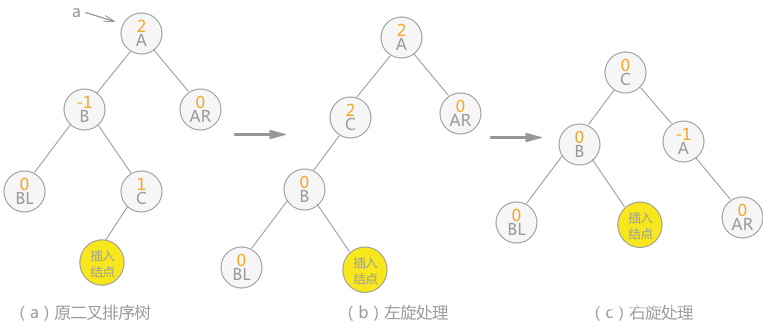
双向旋转(先右后左)平衡处理:如果由于结点 a 的右子树为根结点的左子树上插入结点,导致结点 a 平衡因子由 -1 变为 -2,致使以 a 为根结点的子树失去平衡,则需要进行两次旋转(先右旋后左旋)操作,如下图这种情况:
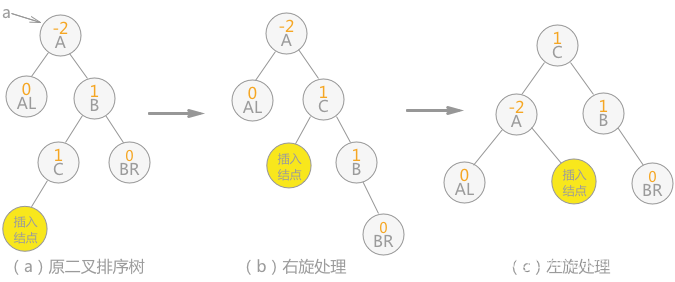
在对查找表{13,24,37,90,53}构建平衡二叉树时,由于符合第 4 条的规律,所以进行先右旋后左旋的处理,最终由不平衡的二叉排序树转变为平衡二叉树。
-
#include <stdio.h>
-
#include <stdlib.h>
-
//分别定义平衡因子数
-
#define LH +1
-
#define EH 0
-
#define RH -1
-
typedef int ElemType;
-
typedef enum {false,true} bool;
-
//定义二叉排序树
-
typedef struct BSTNode{
-
ElemType data;
-
int bf;//balance flag
-
struct BSTNode *lchild,*rchild;
-
}*BSTree,BSTNode;
-
//对以 p 为根结点的二叉树做右旋处理,令 p 指针指向新的树根结点
-
void R_Rotate(BSTree* p)
-
{
-
//借助文章中的图 5 所示加以理解,其中结点 A 为 p 指针指向的根结点
-
BSTree lc = (*p)->lchild;
-
(*p)->lchild = lc->rchild;
-
lc->rchild = *p;
-
*p = lc;
-
}
-
对以 p 为根结点的二叉树做左旋处理,令 p 指针指向新的树根结点
-
void L_Rotate(BSTree* p)
-
{
-
//借助文章中的图 6 所示加以理解,其中结点 A 为 p 指针指向的根结点
-
BSTree rc = (*p)->rchild;
-
(*p)->rchild = rc->lchild;
-
rc->lchild = *p;
-
*p = rc;
-
}
-
//对以指针 T 所指向结点为根结点的二叉树作左子树的平衡处理,令指针 T 指向新的根结点
-
void LeftBalance(BSTree* T)
-
{
-
BSTree lc,rd;
-
lc = (*T)->lchild;
-
//查看以 T 的左子树为根结点的子树,失去平衡的原因,如果 bf 值为 1 ,则说明添加在左子树为根结点的左子树中,需要对其进行右旋处理;反之,如果 bf 值为 -1,说明添加在以左子树为根结点的右子树中,需要进行双向先左旋后右旋的处理
-
switch (lc->bf)
-
{
-
case LH:
-
(*T)->bf = lc->bf = EH;
-
R_Rotate(T);
-
break;
-
case RH:
-
rd = lc->rchild;
-
switch(rd->bf)
-
{
-
case LH:
-
(*T)->bf = RH;
-
lc->bf = EH;
-
break;
-
case EH:
-
(*T)->bf = lc->bf = EH;
-
break;
-
case RH:
-
(*T)->bf = EH;
-
lc->bf = LH;
-
break;
-
}
-
rd->bf = EH;
-
L_Rotate(&(*T)->lchild);
-
R_Rotate(T);
-
break;
-
}
-
}
-
//右子树的平衡处理同左子树的平衡处理完全类似
-
void RightBalance(BSTree* T)
-
{
-
BSTree lc,rd;
-
lc= (*T)->rchild;
-
switch (lc->bf)
-
{
-
case RH:
-
(*T)->bf = lc->bf = EH;
-
L_Rotate(T);
-
break;
-
case LH:
-
rd = lc->lchild;
-
switch(rd->bf)
-
{
-
case LH:
-
(*T)->bf = EH;
-
lc->bf = RH;
-
break;
-
case EH:
-
(*T)->bf = lc->bf = EH;
-
break;
-
case RH:
-
(*T)->bf = EH;
-
lc->bf = LH;
-
break;
-
}
-
rd->bf = EH;
-
R_Rotate(&(*T)->rchild);
-
L_Rotate(T);
-
break;
-
}
-
}
-
-
int InsertAVL(BSTree* T,ElemType e,bool* taller)
-
{
-
//如果本身为空树,则直接添加 e 为根结点
-
if ((*T)==NULL)
-
{
-
(*T)=(BSTree)malloc(sizeof(BSTNode));
-
(*T)->bf = EH;
-
(*T)->data = e;
-
(*T)->lchild = NULL;
-
(*T)->rchild = NULL;
-
*taller=true;
-
}
-
//如果二叉排序树中已经存在 e ,则不做任何处理
-
else if (e == (*T)->data)
-
{
-
*taller = false;
-
return 0;
-
}
-
//如果 e 小于结点 T 的数据域,则插入到 T 的左子树中
-
else if (e < (*T)->data)
-
{
-
//如果插入过程,不会影响树本身的平衡,则直接结束
-
if(!InsertAVL(&(*T)->lchild,e,taller))
-
return 0;
-
//判断插入过程是否会导致整棵树的深度 +1
-
if(*taller)
-
{
-
//判断根结点 T 的平衡因子是多少,由于是在其左子树添加新结点的过程中导致失去平衡,所以当 T 结点的平衡因子本身为 1 时,需要进行左子树的平衡处理,否则更新树中各结点的平衡因子数
-
switch ((*T)->bf)
-
{
-
case LH:
-
LeftBalance(T);
-
*taller = false;
-
break;
-
case EH:
-
(*T)->bf = LH;
-
*taller = true;
-
break;
-
case RH:
-
(*T)->bf = EH;
-
*taller = false;
-
break;
-
}
-
}
-
}
-
//同样,当 e>T->data 时,需要插入到以 T 为根结点的树的右子树中,同样需要做和以上同样的操作
-
else
-
{
-
if(!InsertAVL(&(*T)->rchild,e,taller))
-
return 0;
-
if (*taller)
-
{
-
switch ((*T)->bf)
-
{
-
case LH:
-
(*T)->bf = EH;
-
*taller = false;
-
break;
-
case EH:
-
(*T)->bf = RH;
-
*taller = true;
-
break;
-
case RH:
-
RightBalance(T);
-
*taller = false;
-
break;
-
}
-
}
-
}
-
return 1;
-
}
-
//判断现有平衡二叉树中是否已经具有数据域为 e 的结点
-
bool FindNode(BSTree root,ElemType e,BSTree* pos)
-
{
-
BSTree pt = root;
-
(*pos) = NULL;
-
while(pt)
-
{
-
if (pt->data == e)
-
{
-
//找到节点,pos指向该节点并返回true
-
(*pos) = pt;
-
return true;
-
}
-
else if (pt->data>e)
-
{
-
pt = pt->lchild;
-
}
-
else
-
pt = pt->rchild;
-
}
-
return false;
-
}
-
//中序遍历平衡二叉树
-
void InorderTra(BSTree root)
-
{
-
if(root->lchild)
-
InorderTra(root->lchild);
-
-
printf("%d ",root->data);
-
-
if(root->rchild)
-
InorderTra(root->rchild);
-
}
-
-
int main()
-
{
-
int i,nArr[] = {1,23,45,34,98,9,4,35,23};
-
BSTree root=NULL,pos;
-
bool taller;
-
//用 nArr查找表构建平衡二叉树(不断插入数据的过程)
-
for (i=0;i<9;i++)
-
{
-
InsertAVL(&root,nArr[i],&taller);
-
}
-
//中序遍历输出
-
InorderTra(root);
-
//判断平衡二叉树中是否含有数据域为 103 的数据
-
if(FindNode(root,103,&pos))
-
printf("\n%d\n",pos->data);
-
else
-
printf("\nNot find this Node\n");
-
return 0;
-
}
文章来源: allen5g.blog.csdn.net,作者:CodeAllen的博客,版权归原作者所有,如需转载,请联系作者。
原文链接:allen5g.blog.csdn.net/article/details/117002112
- 点赞
- 收藏
- 关注作者


评论(0)