如何在 Python 中实现贝叶斯网络？– 用例子解释贝叶斯网络

贝叶斯网络已经塑造了提供有限信息和资源的复杂问题。它正在该时代最先进的技术中实施，例如人工智能和机器学习。拥有这样一个系统是当今以技术为中心的世界的需要。牢记这一点，本文完全致力于介绍贝叶斯网络的工作原理以及如何应用它们来解决复杂的问题。

这是我将要讨论的主题列表 在此博客中：

1. 什么是贝叶斯网络？
2. 什么是有向无环图？
3. 贝叶斯网络背后的数学
4. 用一个例子理解贝叶斯网络
5. 在 Python 中实现贝叶斯网络
6. 贝叶斯网络应用

什么是贝叶斯网络？

贝叶斯网络属于概率图形建模 (PGM) 技术的范畴，该技术用于通过使用概率的概念来计算不确定性。贝叶斯网络通常被称为信念网络，用于通过使用以下方法对不确定性进行建模有向无环图(DAG)。

这给我们带来了一个问题：

什么是有向无环图？

有向无环图用于表示贝叶斯网络，与任何其他统计图一样，DAG 包含一组节点和链接，其中链接表示节点之间的关系。

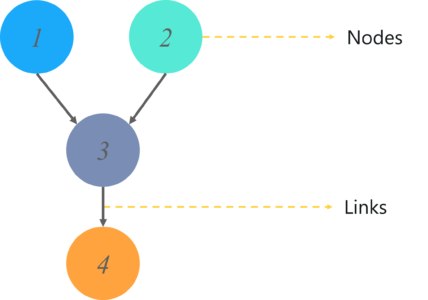
这里的节点代表随机变量，边定义了这些变量之间的关系。但是这些图模型是什么？你可以从 DAG 得到什么输出？

DAG 基于每个随机变量的条件概率分布(CDP) 对发生的事件的不确定性进行建模。使用条件概率表(CPT)来表示网络中每个变量的 CPD。

在我们继续之前，让我们了解贝叶斯网络背后的基本数学。

贝叶斯网络背后的数学

如前所述，贝叶斯模型基于简单的概率概念。那么让我们了解条件概率和联合概率分布的含义。

什么是联合概率？

联合概率是两个或多个事件同时发生的统计量度，即 P(A, B, C)，事件 A、B 和 C 发生的概率。它可以表示为两个或多个事件发生交叉的概率。

什么是条件概率？

事件 X 的条件概率是在事件 Y 已经发生的情况下该事件将发生的概率。

p(X| Y) 是事件 X 发生的概率，给定该事件，Y 发生。

• 如果 X 和 Y 是相关事件，则条件概率的表达式为：
  P (X| Y) = P (X and Y) / P (Y)
• 如果 A 和 B 是独立事件，则条件概率的表达式为：
  P(X| Y) = P (X)

要了解有关统计和概率概念的更多信息，您可以阅读此内容，您需要了解的有关统计和概率的所有信息 博客。

现在让我们看一个例子来了解贝叶斯网络的工作原理。

贝叶斯网络示例

假设我们正在创建一个贝叶斯网络，它将模拟学生在考试中的分数 (m)。分数将取决于：

1. 考试级别（e）：这是一个可以取两个值的离散变量，（难，易）

2. 学生的智商 (i)：一个可以取两个值（高、低）的离散变量

分数将预测他/她是否会被 (a) 大学录取。

智商还将预测学生的能力得分。

有了这些信息，我们就可以构建一个贝叶斯网络来模拟学生在考试中的表现。贝叶斯网络可以表示为 DAG，其中每个节点表示一个预测学生表现的变量。

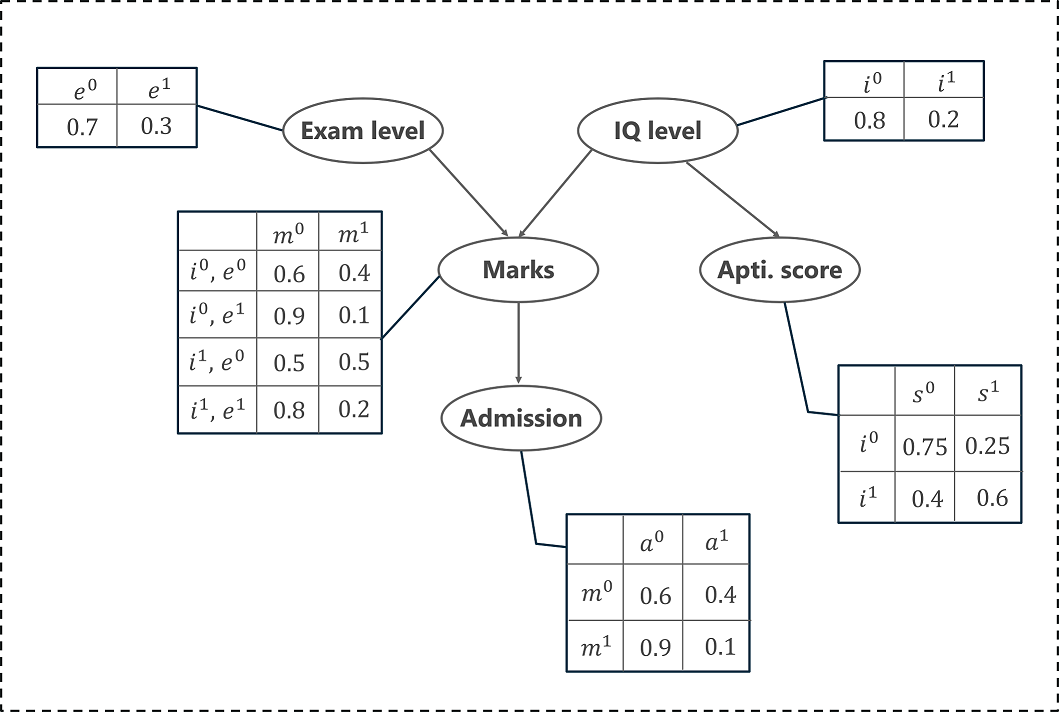
上面我通过 DAG 和条件概率表表示了这个分布。我们现在可以计算这 5 个变量的联合概率分布，即条件概率的乘积：

这里，

• p(a | m) 表示学生根据他的分数获得录取的条件概率。

• p(m | I, e) 表示给定他的智商水平和考试水平的学生分数的条件概率。

• p(i) 表示他的智商水平（高或低）的概率

• p(e) 表示考试级别的概率（难或易）

• p(s | i) 表示他的能力得分的条件概率，给定他的智商水平

DAG 清楚地显示了每个变量（节点）如何依赖于其父节点，即学生的分数取决于考试水平（父节点）和 IQ 水平（父节点）。同样，能力得分取决于智商水平（父节点），最后，他被大学录取取决于他的分数（父节点）。这种关系由 DAG 的边表示。

如果您仔细观察，我们可以在这里看到一个模式。随机变量的概率取决于他的父母。因此，我们可以将贝叶斯网络表述为：

其中，X_i 表示随机变量，其概率取决于父节点的概率，𝑃𝑎𝑟𝑒𝑛𝑡𝑠(𝑋_𝑖)。

很简单，不是吗？

贝叶斯网络是最简单但有效的技术之一，可应用于预测建模、描述性分析等 在。

为了让事情更清楚，让我们使用 Python 从头开始​​构建一个贝叶斯网络。

贝叶斯网络 Python

在这个演示中，我们将使用贝叶斯网络来解决著名的蒙蒂霍尔问题。对于那些不知道蒙蒂霍尔问题是什么的人，让我解释一下：

以电视连续剧“让我们做一笔交易”的主持人命名的蒙蒂霍尔问题是一个悖论的概率难题，十多年来一直困扰着人们。

所以这就是它的工作原理。游戏涉及三扇门，其中一扇门后面是一辆汽车，其余两扇门后面有山羊。所以你从随机选择一扇门开始，比如#2。另一方面，主人知道汽车藏在哪里，他打开另一扇门，说#1（后面有一只山羊）。问题来了，你现在有一个选择，主持人会问你是否要选择门 #3 而不是你的第一选择，即 #2。

如果你改变你的选择，还是应该坚持你的第一选择更好？

这正是我们要建模的。如果参与者决定改变他的选择，我们将创建一个贝叶斯网络来了解获胜的概率。

在我们开始演示之前简短的免责声明。

我将使用 Python 来实现贝叶斯网络，如果您不了解 Python，可以阅读以下博客：

1. Python 教程——学习 Python 编程的完整指南
2. Python 编程语言——从 Python 基础开始
3. Python 函数初学者指南
4. 用于数据科学的 Python

现在让我们开始吧。

第一步是构建一个有向无环图。

该图具有三个节点，每个节点代表通过以下方式选择的门：

1. 客人选择的门
2. 装有奖品的门（车）
3. 蒙蒂选择打开的门

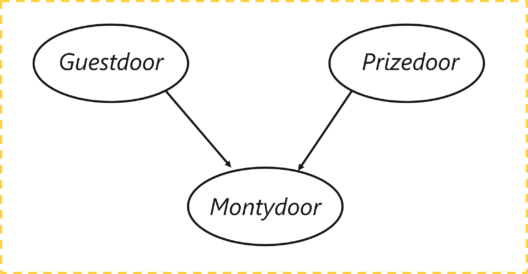
让我们了解这里的依赖关系，客人选择的门和包含汽车的门是完全随机的过程。但是，Monty 选择打开的门取决于两扇门；客人选择的门，奖品在后面的门。蒙蒂必须选择这样一种方式，即门中没有奖品，也不能是客人选择的那个。

#Import required packages
import math
from pomegranate import *
 
# Initially the door selected by the guest is completely random
guest =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
 
# The door containing the prize is also a random process
prize =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
 
# The door Monty picks, depends on the choice of the guest and the prize door
monty =ConditionalProbabilityTable(
[[ 'A', 'A', 'A', 0.0 ],
[ 'A', 'A', 'B', 0.5 ],
[ 'A', 'A', 'C', 0.5 ],
[ 'A', 'B', 'A', 0.0 ],
[ 'A', 'B', 'B', 0.0 ],
[ 'A', 'B', 'C', 1.0 ],
[ 'A', 'C', 'A', 0.0 ],
[ 'A', 'C', 'B', 1.0 ],
[ 'A', 'C', 'C', 0.0 ],
[ 'B', 'A', 'A', 0.0 ],
[ 'B', 'A', 'B', 0.0 ],
[ 'B', 'A', 'C', 1.0 ],
[ 'B', 'B', 'A', 0.5 ],
[ 'B', 'B', 'B', 0.0 ],
[ 'B', 'B', 'C', 0.5 ],
[ 'B', 'C', 'A', 1.0 ],
[ 'B', 'C', 'B', 0.0 ],
[ 'B', 'C', 'C', 0.0 ],
[ 'C', 'A', 'A', 0.0 ],
[ 'C', 'A', 'B', 1.0 ],
[ 'C', 'A', 'C', 0.0 ],
[ 'C', 'B', 'A', 1.0 ],
[ 'C', 'B', 'B', 0.0 ],
[ 'C', 'B', 'C', 0.0 ],
[ 'C', 'C', 'A', 0.5 ],
[ 'C', 'C', 'B', 0.5 ],
[ 'C', 'C', 'C', 0.0 ]], [guest, prize] )
 
d1 = State( guest, name="guest" )
d2 = State( prize, name="prize" )
d3 = State( monty, name="monty" )
 
#Building the Bayesian Network
network = BayesianNetwork( "Solving the Monty Hall Problem With Bayesian Networks" )
network.add_states(d1, d2, d3)
network.add_edge(d1, d3)
network.add_edge(d2, d3)
network.bake()

上面代码中'A'、'B'、'C'分别代表客人选择的门、奖品门和蒙蒂选择的门。在这里，我们绘制了每个节点的条件概率。由于奖品门和客人门是随机挑选的，因此无需考虑太多。但是，Monty 选择的门取决于其他两个门，因此在上面的代码中，我已经考虑了所有可能的情况得出了条件概率。

下一步是使用此模型进行预测。贝叶斯网络的优势之一是它们能够根据“观察变量”的值推断任意“隐藏变量”的值。这些隐藏变量和观察变量不需要事先指定，观察到的变量越多，对隐藏变量的推断就越好。

现在我们已经建立了模型，是时候进行预测了。

beliefs = network.predict_proba({ 'guest' : 'A' })
beliefs = map(str, beliefs)
print("n".join( "{}t{}".format( state.name, belief ) for state, belief in zip( network.states, beliefs ) ))
 
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333333,
"B" :0.3333333333333333,
"C" :0.3333333333333333
}
],
}
 
monty {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"C" :0.49999999999999983,
"A" :0.0,
"B" :0.49999999999999983
}
],
}

在上面的代码片段中，我们假设客人选择了门“A”。鉴于此信息，奖品门为“A”、“B”、“C”的概率相等（1/3），因为这是一个随机过程。但是，Monty 选择“A”的概率显然为零，​​因为客人选择了“A”门。另外两扇门有 50% 的几率被蒙蒂选中，因为我们不知道哪个是奖门。

beliefs = network.predict_proba({'guest' : 'A', 'monty' : 'B'})
print("n".join( "{}t{}".format( state.name, str(belief) ) for state, belief in zip( network.states, beliefs )))
 
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333334,
"B" :0.0,
"C" :0.6666666666666664
}
],
}
monty B

在上面的代码片段中，我们为贝叶斯网络提供了两个输入，这就是事情变得有趣的地方。我们提到了以下几点：

1. 客人选择门'A'
2. 蒙蒂选择门“B”

注意输出，汽车在门“C”后面的概率约为。66%。这证明如果客人改变他的选择，他有更高的获胜概率。虽然这对你们中的一些人来说可能看起来很混乱，但众所周知的事实是：

• 决定换门的客人赢得了大约 2/3 的时间
• 拒绝转换的客人赢得了大约 1/3 的时间

在这种情况下使用贝叶斯网络 这涉及预测不确定的任务和结果。在下面的部分中，您将了解如何使用贝叶斯网络来解决更多此类问题。

贝叶斯网络应用

贝叶斯网络在医疗保健、医学、生物信息学、信息检索等各个领域有着无数的应用。以下是贝叶斯网络的实际应用列表：

1. 疾病诊断：贝叶斯网络常用于医学领域的疾病检测和预防。它们可用于对可能的症状进行建模并预测一个人是否患病。

2. 优化的 Web 搜索：贝叶斯网络用于通过了解搜索意图并提供最相关的搜索结果来提高搜索准确性。它们可以有效地将用户意图映射到相关内容并提供搜索结果。

3. 垃圾邮件过滤：贝叶斯模型已在 Gmail 垃圾邮件过滤算法中使用多年。他们可以通过理解邮件的上下文含义来有效地对文档进行分类。它们还用于其他文档分类应用程序。

4. 基因调控网络： GRN 是由许多 DNA 片段组成的基因网络。它们被有效地用于直接或间接与细胞的其他部分进行通信。贝叶斯网络等数学模型用于对此类细胞行为进行建模以形成预测。

5. 生物监测： 贝叶斯网络在监测药物中使用的化学瞌睡量方面发挥着重要作用。

既然您知道贝叶斯网络的工作原理，我相信您很想了解更多信息。以下博客列表可帮助您开始了解其他统计概念：

1. 数据科学数学和统计学完整指南
2. 您需要了解的有关统计和概率的所有信息
3. 带例子的马尔可夫链介绍 – 马尔可夫链与 Python