一、算法详细讲解

1.0 前言介绍

讲解已经非常详细，尽量是让小白都能学会，因此如果你觉得自己算法并不是很好，或者没有基础，那我希望你一定要认真看我写的每一句话，同时要学会自己思考，不然对你也收获不大。

1.1二分查找介绍

二分查找也叫做折半查找。查找也是有特殊情况的，比如数列本身是有序的。这个有序数列是怎么产生的呢？有时它可能本身就是有序的，也有可能是我们通过之前所学的排序算法得到的。

1.2二分查找条件

由上面的讲解可以知道，二分查找有两个要：，一个是数列有序，另一个是数列使用顺序存储结构（比如数组）

二、 原理及实现

二分查找的实现原理非常简单，首先要有一个有序的列表。但是如果没有，则该怎么办？可以使用排序算法进行排序。
以升序数列为例，比较一个元素与数列中的中间位置的元素的大小，如果比中间位置的元素大，则继续在后半部分的数列中进行二分查找；如果比中间位置的元素小，则在数列的前半部分进行比较；如果相等，则找到了元素的位置。每次比较的数列长度都会是之前数列的一半，直到找到相等元素的位置或者最终没有找到要找的元素。

三、时间复杂度

我们先来想象一下，如果数列中有 3 个数，则先与第 2 个数进行比较，如果比第 2 个数大，则与第 2 个数右边的数列进行二分查找，这时这个数列就剩下一个数了，直接比较是否相等即可。所以在 3 个数的时候最多比较两次。

同理，在有 4 个数的时候，我们与中间数进行比较，一般中间数是首加末除以 2 算出来的，这时我们算出来的中间数是 (1+4)/2 等于 2，所以我们把要查找的数与第 2 个数比较，若比第 2 个数小，则直接与第 1 个数比较；否则与后面两个数进行二分查找，这时的中间数是 (3+4)/2 等于 3，也就是后半部分的第 1 个数。再接着进行比较，相等则找到相应的元素，小于则没有这个数（因为左边所有的数都已经判断过了），大于则继续向右查找。所以在 4 个数的时候最多比较 3 次。
以此类推，在 5 个数的时候最多查找 3 次，在 6 个数的时候也是最多查找 3 次。
时间复杂度：O(logN)

四、算法

画个图便于理解，我把一整个数组划分为三个部分，头部，尾部，中部。

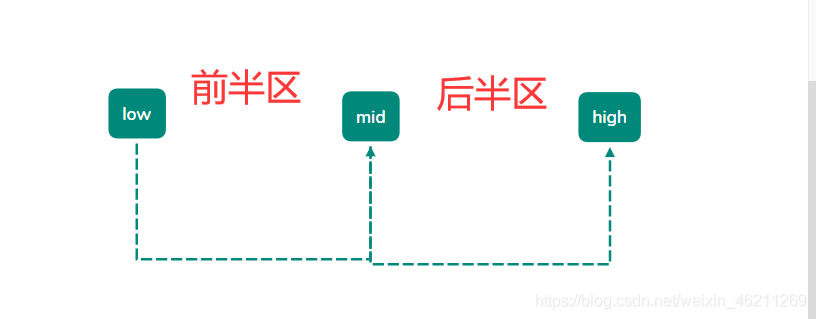
我们每一次查找要么在后半区查找，要么在前半区查找。比如我要在前半区查找，那后半区我们就不要了，high就要移动到mid前一个，mid就要移动到low与mid之间。也就是形成一个新的减半数组。

4.1非递归思想

算法如下，具体再看注释：

//非递归思想
int search(SeqList r, int k)
{//在r[1....n]中查找k
    low = 1; high = n;
    while (low <= high)
    {
        mid = (low + high) / 2;
        if (k == r[mid].key)   return mid;//找到待查元素
        else if (k > r[mid].key)  low = mid + 1;//在后半区查找
        else high = mid - 1;//继续在前半区查找

    }
    return 0;//查找失败返回0
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
 

4.2递归思想

算法如下，具体再看注释：

//递归思想
in search1(SwqList r, int k, in low, int high)
{
    if (low > high) return 0;//排除不合法数组
    mid = (low + high) / 2;
    if (k == r[mid].key)  return mid;//找到待查找元素
    else if (k > r[mid].key)
        return search1(r, k, mid + 1, high);//low变成了原来的mid前，继续查找后半区
    else
        return search1(r, k, low, mid - 1);//继续查找前半区
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
 

五、Leecode案例

5.1例一

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。
示例1：

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

  

 

  
1
  
2
  
3
 

示例2：

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

  

 

  
1
  
2
  
3
 

我们套上面讲的算法模板，代码为：

int search(int* r, int n, int k)
{//在r[1....n]中查找k
   int low = 0;int high = n-1;
    while (low <= high)
    {
        int mid = (low + high) / 2;
        if (k == r[mid])   return mid;//找到待查元素
        else if (k > r[mid])  low = mid + 1;//在后半区查找
        else high = mid - 1;//继续在前半区查找

    }
    return -1;//查找失败返回0
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
 

执行结果：

5.2案例二

套算法模板！！！
题目：你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, …, n]，你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。
代码：

int firstBadVersion(int n) {
    int left = 1, right = n;
    while (left < right) {  // 循环直至区间左右端点相同
        int mid = left + (right - left) / 2;  // 防止计算时溢出
        if (isBadVersion(mid)) {
            right = mid;  // 答案在区间 [left, mid] 中
        } else {
            left = mid + 1;  // 答案在区间 [mid+1, right] 中
        }
    }
    // 此时有 left == right，区间缩为一个点，即为答案
    return left;
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
 

执行返回：

5.3案例三

题目：给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。请必须使用时间复杂度为 O(log n) 的算法。
还是套模板：

int searchInsert(int* nums, int numsSize, int target) {
    int left = 0, right = numsSize - 1, ans = numsSize;
    while (left <= right) {
        int mid = ((right - left) >> 1) + left;
        if (target <= nums[mid]) {
            ans = mid;
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return ans;
}


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
 

返回：

六、 总结

二分查找就是一个静态的方法查表，折半比较，该方法的好处就是比较次数少，查找速度快，效率高。缺点就是必须要有序表，或者我们需要用排序方法先让它变成有序表。二分查找适用于不经常变动而查找频繁的有序表。
我是川川，如果能帮到你，那就在幸运不过了，一起加油！

文章来源: chuanchuan.blog.csdn.net，作者：川川菜鸟，版权归原作者所有，如需转载，请联系作者。

原文链接：chuanchuan.blog.csdn.net/article/details/119892508