简介

Bitmaps、HyperLogLog、Geospatial是Redis的三大特殊数据类型，其中Bitmaps严格来说不能算一种数据类型。Bitmaps、HyperLogLog、Geospatial能轻松的解决很多问题，也是大厂面试中经常会考究的知识点。下文详细的讲述了Bitmaps、HyperLogLog、Geospatial的原理、使用等等。有需要的可以一键三连，如果有什么问题欢迎留言交流，看到一定及时回复。

一、Bitmaps

1、简介

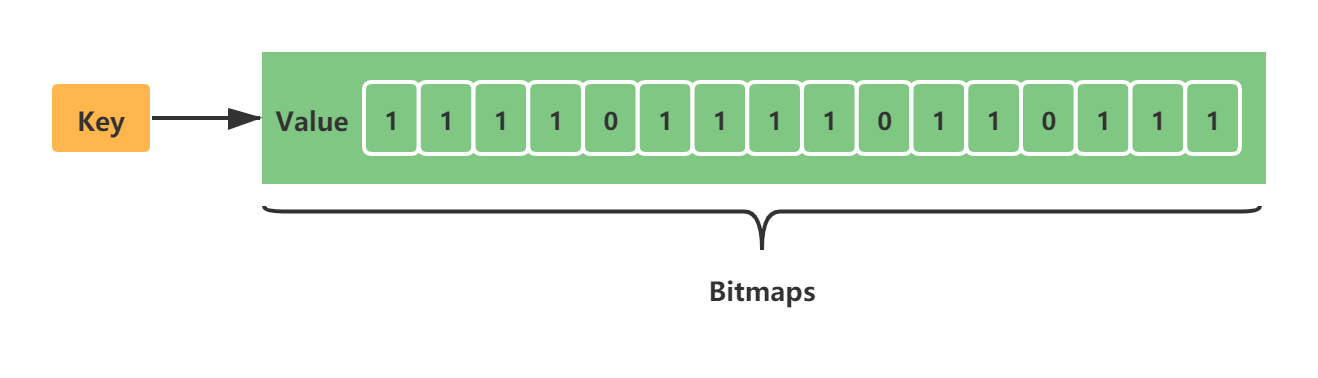
Bitmaps 称为位图，它不是一种数据类型。网上很多视频教程把Bitmaps称为数据类型，应该是不正确的。Bitmaps 是Redis提供给使用者用于操作位的“数据类型”。它主要有如下的基本特性：

• Bitmaps 不是数据类型，底层就是字符串（key-value），byte数组。我们可以使用普通的get/set直接获取和设值位图的内容，也可以通过Redis提供的位图操作getbit/setbit等将byte数组看成“位数组”来处理
• Bitmaps 的“位数组”每个单元格只能存储0和1，数组的下标在Bitmaps中称为偏移量

• Bitmaps设置时key不存在会自动生成一个新的字符串，如果设置的偏移量超出了现有内容的范围，就会自动将位数组进行零扩充

2 、基本操作

2.1 SETBIT key offset value

对key存储的字符串，设置或者清除指定偏移量上的位（bit），位的设置或者清除取决于value参数，0/1；当key不存在时，自动生成一个新的字符串。字符串会进行伸展确保value保存在指定的偏移量上。字符串进行伸展时，空白位置以0填充。

时间复杂度 :

offset 范围：

返回值：

案例：

使用Bitmaps来存储用户是否打卡，打卡记做1，未打卡为0，用户的id作为偏移量

假设存在10个用户，此时用户1、3、5、9、10打了卡，其他人未打卡，Bitmaps的初始化结果如下所示：

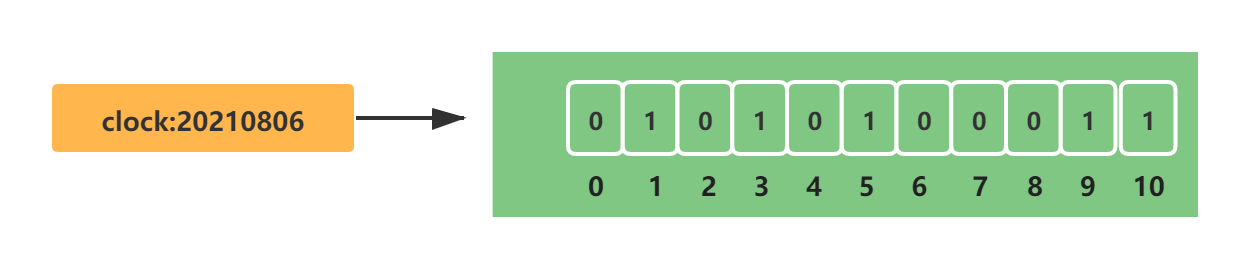
clock:20210806代表2021/08/06的打卡记录

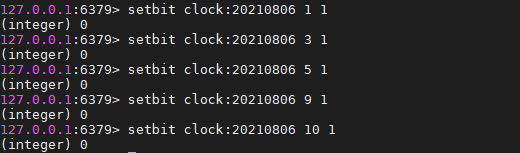
注意事项：

正式系统中，id肯定不会是0、1、2这种，而是以某一个数组开头，比如1000000000000001、1000000000000002这个时候非常容易导致偏移量的浪费，因此我们可以考虑通过计算减去一个合适的值后再设置偏移量，如果设置的Bitmaps偏移量过大，容易造成分配内存时间过长，Redis服务器被阻塞。

2.2 GETBIT key offset

获取指定偏移量上的位（bit），当offset比字符串长度大，或者key不存在，返回0；

时间复杂度：

返回值：

字符串值指定偏移量上的位（bit）

案例：

clock:20210806代表2021/08/06的打卡记录

2.3 BITCOUNT key [start] [end]

计算给定字符串中，被设置为1的bit位的数量。start和end参数可以指定查询的范围，可以使用负数值。-1代表最后一个字节，-2代表倒是第二个字节。

注意：start和end是字节索引，因此每增加1 代表的是增加一个字符，也就是8位，所以位的查询范围必须是8的倍数。

时间复杂度：

返回值：

被设置为1的位的数量

案例：

clock:20210806代表2021/08/06的打卡记录，此时一共11位，前8位置3个1，后3位中2个1

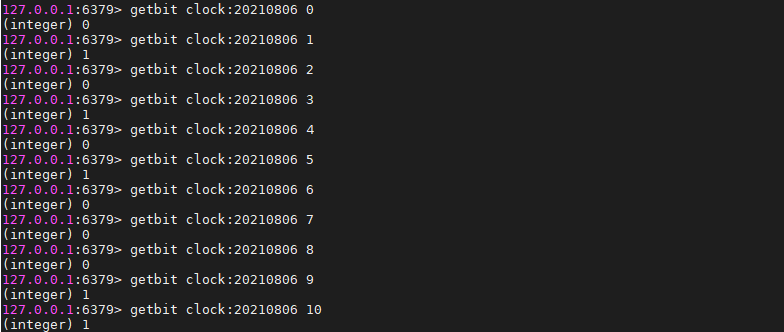
bitcount clock:20210806 0 0 表示第1个字符中1的个数

bitcount clock:20210806 1 1 表示第2个字符中1的个数

bitcount clock:20210806 0 1 表示第1和第2个字符中1的个数

2.4 BITPOS key bit [start] [end]

返回第一个置为bit的二进制位的位置，默认检测整个Bitmaps，也可以通过start和end参数指定查询范围

注意：start和end是字节索引，因此每增加1 代表的是增加一个字符，也就是8位，所以位的查询范围必须是8的倍数。

时间复杂度：

返回值：

整数回复

案例：

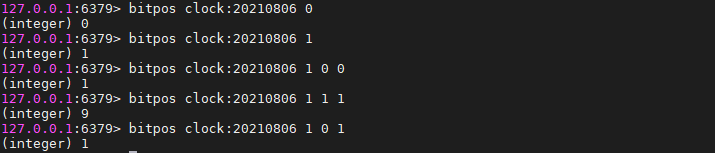
bitpos clock:20210806 0 表示第一个0的位置

bitpos clock:20210806 1 表示第一个1的位置

bitpos clock:20210806 1 0 0 表示第一个字符中，第一个1的位置

bitpos clock:20210806 1 1 1 表示第二个字符中，第一个1的位置

bitpos clock:20210806 1 0 1 表示第一个和第二个字符中，第一个1的位置

2.5 BITOP operation destkey key [key …]

Redis的Bitmaps提供BITOP指令来对一个或多个（除了NOT操作）二进制位的字符串key进行位元操作，操作的结果保存到destkey上，operation是操作类型，有四种分别是：AND、OR、NOT、XOR

• BITOP AND destkey key [key ...] ，对一个或多个 key 求逻辑并，并将结果保存到 destkey
• BITOP OR destkey key [key ...] ，对一个或多个 key 求逻辑或，并将结果保存到 destkey 

• BITOP XOR destkey key [key ...] ，对一个或多个 key 求逻辑异或，并将结果保存到 destkey
• BITOP NOT destkey key ，对给定 key 求逻辑非，并将结果保存到 destkey

当字符串长度不一致是，较短的那个字符串所缺失的部分会被看作0，空的key也会被看作是包含0的字符串序列

时间复杂度：

返回值：

位运算的结果（保存到destkey的字符串的长度和输入key中的最长的字符串的长度相等）

案例：

这里使用key1 1001和key2 1011进行上述四种操作

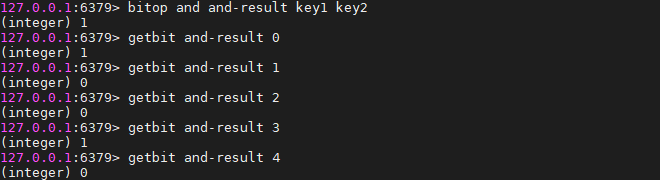
BITOP AND destkey key [key ...] 

运算规则：0&0=0;   0&1=0;    1&0=0;     1&1=1;       

即：两位同时为“1”，结果才为“1”，否则为0

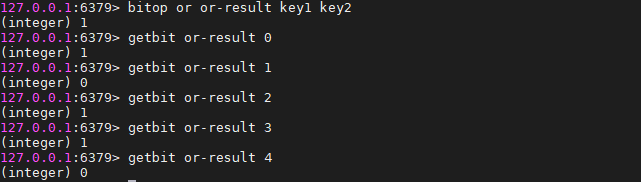
BITOP OR destkey key [key ...] 

运算规则：0|0=0；   0|1=1；   1|0=1；    1|1=1； 　　

即 ：参加运算的两个对象只要有一个为1，其值为1

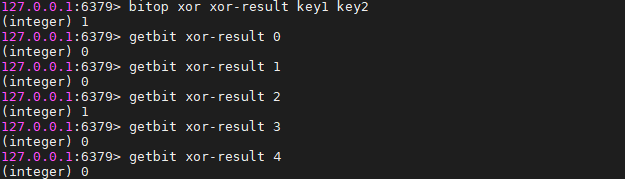
BITOP XOR destkey key [key ...]

运算规则：0^0=0；   0^1=1；   1^0=1；   1^1=0；　　

即：参加运算的两个对象，如果两个相应位为“异”（值不同），则该位结果为1，否则为0

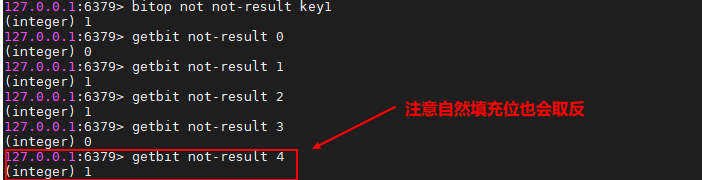
BITOP NOT destkey key 

运算规则：取反

2.6 BITFIELD key [GET type offset] [SET type offset value] [INCRBY type offset increment] [OVERFLOW WRAP|SAT|FAIL]

2.1和2.2中的setbit和getbit都是对指定key的单个位的操作，如果需要对多个位同时操作，那么可以使用bitfield指令，bitfield有三个子指令，分别是get、set、incrby，它们可以对指定的片段进行读写，但是最多处理64个连续的位，超过64个连续的位，需要使用多个子指令，bitfield可以同时执行多个子指令（无符号整数只能返回63位）。

注意：

• 使用 GET 子命令对超出字符串当前范围的二进制位进行访问（包括键不存在的情况）， 超出部分的二进制位的值将被当做是 0 。
• 使用 SET 子命令或者 INCRBY 子命令对超出字符串当前范围的二进制位进行访问将导致字符串被扩大， 被扩大的部分会使用值为 0 的二进制位进行填充。 在对字符串进行扩展时， 命令会根据字符串目前已有的最远端二进制位， 计算出执行操作所需的最小长度。

值操作子指令：

• GET <type> <offset> —— 返回指定的二进制位范围
• SET <type> <offset> <value> —— 对指定的二进制位范围进行设置，并返回它的旧值

• INCRBY <type> <offset> <increment> —— 对指定的二进制位范围执行加法操作，并返回它的旧值。用户可以通过向 increment 参数传入负值来实现相应的减法操作

溢出策略子指令：

• WRAP：回绕/折返（wrap around）-默认溢出策略，对于无符号整数来说， 回绕就像使用数值本身与能够被储存的最大无符号整数执行取模计算， 这也是 C 语言的标准行为。 对于有符号整数来说， 上溢将导致数字重新从最小的负数开始计算， 而下溢将导致数字重新从最大的正数开始计算。
• SAT：饱和计算（saturation arithmetic），也可以理解为饱和截断，这种模式下下溢计算的结果为最小的整数值， 而上溢计算的结果为最大的整数值

• FAIL：失败不执行，这种模式会拒绝执行那些导致上溢或者下溢的计算情况，返回nil表示计算未被执行。

需要注意的是， OVERFLOW 子命令只会对紧随着它之后被执行的 INCRBY 命令产生效果， 这一效果将一直持续到与它一同被执行的下一个 OVERFLOW 命令为止。 在默认情况下， INCRBY 命令使用 WRAP 方式来处理溢出计算。

i与u:

i表示有符号整数，u表示无符号整数。u4代表4位长的无符号整数，i8代表8位长的有符号整数。

案例：

测试数字为10100111

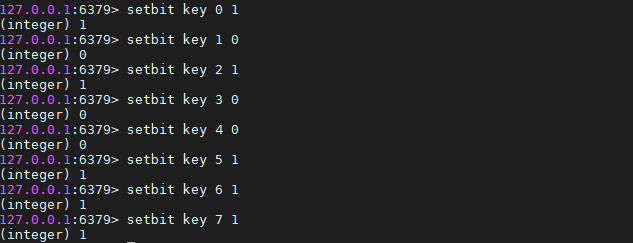
bitfield key get u4 0 从第一个位开始取4个位，得到无符号数1010=10

bitfield key set u8 0 128 从第0个开始，将接下来的8位用无符号整数128替换，也就是10000000

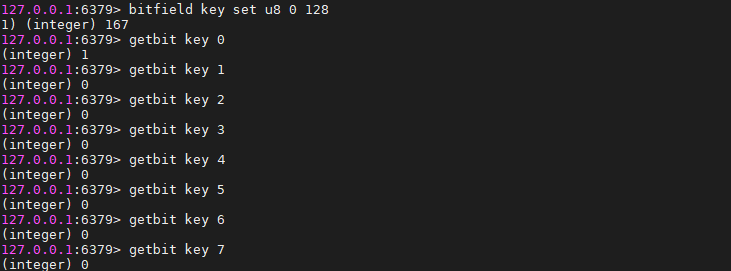
bitfield key incrby u4 2 1 从第2位开始对接下来的4位无符号数+1

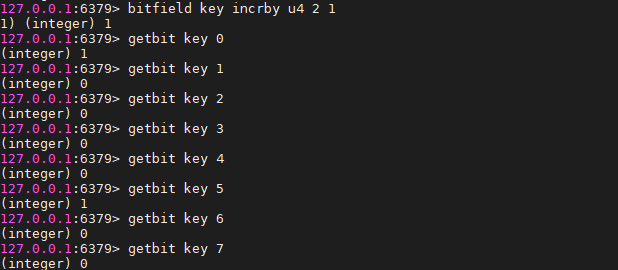
bitfield key set u8 0 128 get u4 0 incrby u4 2 1 复合指令，是上面三者的组成，返回值是每个操作的子集，相当于管道操作

二、HyperLogLog

1、简介

首先抛出一个业务问题：

假设产品经理让你设计一个模块，来统计PV（Page View页面的访问量），那么你会怎么做？

我想很多人对于PV（Page View页面的访问量）的统计会很快的想到使用Redis的incr、incrby指令，给每个网页配置一个独立Redis计数器就可以了，把这个技术区的key后缀加上当它的日期，这样一个请求过来，就可以通过执行incr、incrby指令统计所有PV。

此时当你完成这个需求后，产品经理又让你设计一个模块，统计UV（Unique Visitor，独立访客），那么你又会怎么做呢？

UV与PV不一样，UV需要根据用户ID去重，如果用户没有ID我们可能需要考虑使用用户访问的IP或者其他前端穿过了的唯一标志来区分，此时你可能会想到使用如下的方案来统计UV。

1. 存储在MySQL数据库表中，使用distinct count计算不重复的个数
2. 使用Redis的set、hash、bitmaps等数据结构来存储，比如使用set，我们可以使用用户ID，通过sadd加入set集合即可

但是上面的两张方案都存在两个比较大的问题：

1. 随着数据量的增加，存储数据的空间占用越来越大，对于非常大的页面的UV统计，基本不合实际
2. 统计的性能比较慢，虽然可以通过异步方式统计，但是性能并不理想

因此针对UV的统计，我们将会考虑使用Redis的新数据类型HyperLogLog.

HyperLogLog是用来做基数统计的算法，它提供不精确的去重计数方案（这个不精确并不是非常不精确），标准误差是0.81%，对于UV这种统计来说这样的误差范围是被允许的。HyperLogLog的优点在于，输入元素的数量或者体积非常大时，基数计算的存储空间是固定的。在Redis中，每个HyperLogLog键只需要花费12KB内存，就可以计算接近2^64个不同的基数。

但是：HyperLogLog只能统计基数的大小（也就是数据集的大小，集合的个数），他不能存储元素的本身，不能向set集合那样存储元素本身，也就是说无法返回元素。

HyperLogLog指令都是pf(PF)开头，这是因为HyperLogLog的发明人是Philippe Flajolet，pf是他的名字的首字母缩写。

2、命令

2.1 PFADD key element [element …]

将任意数量的元素添加到指定的 HyperLogLog 里面，当PFADD key element [element …]指令执行时，如果HyperLogLog的估计近似基数在命令执行之后出现了变化，那么命令返回1，否则返回0，如果HyperLogLog命令执行时给定的键不存在，那么程序将先创建一个空的HyperLogLog结构，再执行命令。

该命令可以只给定key不给element，这种以方式被调用时：

• 如果给定的键存在且已经是一个HyperLogLog，那么这种调用不会产生任何效果
• 如果给定的键不存在，那么命令会闯进一个空的HyperLogLog，并且给客户端返回1

返回值：

如果HyperLogLog数据结构内部存储的数据被修改了，那么返回1，否则返回0

时间复杂度：

O(1)

使用示例：

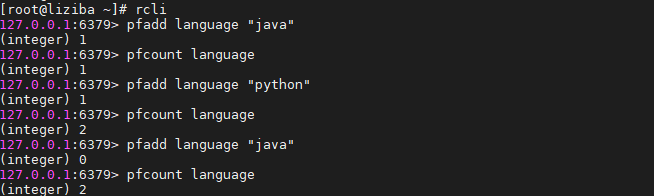
2.2 PFCOUNT key [key …]

PFCOUNT 指令后面可以跟多个key，当PFCOUNT key [key …]命令作用于单个键时，返回存储在给定键的HyperLogLog的近似基数，如果键不存在，则返回0；当PFCOUNT key [key …]命令作用于多个键时，返回所给定HyperLogLog的并集的近似基数，这个近似基数是通过将索引给定HyperLogLog合并至一个临时HyperLogLog来计算得出的。

返回值：

返回给定HyperLogLog包含的唯一元素的近似数量的整数值

时间复杂度：

当命令作用于单个HyperLogLog时，时间复杂度为O(1)，并且具有非常低的平均常数时间。当命令作用于N个HyperLogLog时，时间复杂度为O(N)，常数时间会比单个HyperLogLog要大的多。

使用示例：

2.3 PFMERGE destkey sourcekey [sourcekey …]

将多个HyperLogLog合并到一个HyperLogLog中，合并后HyperLogLog的基数接近于所有输入HyperLogLog的可见集合的并集，合并后得到的HyperLogLog会被存储在destkey键里面，如果该键不存在，那么命令在执行之前，会先为该键创建一个空的HyperLogLog。

返回值：

字符串回复，返回OK

时间复杂度：

O(N)，其中N为被合并的HyperLogLog的数量，不过这个命令的常数复杂度比较高

使用示例：

3、原理

3.1 伯努利试验

HyperLogLog的算法设计能使用12k的内存来近似的统计2^64个数据，这个和伯努利试验有很大的关系，因此在探究HyperLogLog原理之前，需要先了解一下伯努利试验。

以下是百度百科关于伯努利试验的介绍：

伯努利试验是数据概率论中的一部分，它的典故源于“抛硬币”。

一个硬币只有正面和反面，每次抛硬币出现正反面的概率都是50%，我们一直抛硬币直到出现第一次正面为止，记录抛硬币的次数，这个就被称为一次伯努利试验。伯努利试验需要做非常多的次数，数据才会变得有意义。

对于n次伯努利试验，出现正面的次数为n，假设每次伯努利试验抛掷的次数为k（也就是每次出现正面抛掷的次数），第一次伯努利试验抛掷次数为k1，第n次伯努利试验抛掷次数为kn，在这n次伯努利试验中，抛掷次数最大值为kmax。

上述的伯努利试验，结合极大似然估算方法（极大似然估计），得出n和kmax之间的估算关系：n=2^kmax。很显然这个估算关系是不准确的，例如如下案例：

第一次试验：抛掷1次出现正面，此时k=1,n=1;

第二次实验：抛掷3次出现正面，此时k=3,n=2;

第三次实验：抛掷6次出现正面，此时k=6,n=3;

第n次试验：抛掷10次出现正面，此时k=10,n=n,通过估算关系计算，n=2^10

上述案例可以看出，假设n=3，此时通过估算关系n=2^kmax，2^6 ≠3，而且偏差很大。因此得出结论，这种估算方法误差很大。

3.2 估值优化

关于上述估值偏差较大的问题，可以采用如下方式结合来缩小误差：

1. 增加测试的轮数，取平均值。假设三次伯努利试验为1轮测试，我们取出这一轮试验中最大的的kmax作为本轮测试的数据，同时我们将测试的轮数定位100轮，这样我们在100轮实验中，将会得到100个kmax，此时平均数就是(k_max_1 + ... + k_max_m)/m，这里m为试验的轮数，此处为100.
2. 增加修正因子，修正因子是一个不固定的值，会根据实际情况来进行值的调整。

上述这种增加试验轮数，去kmax的平均值的方法，是LogLog算法的实现。因此LogLog它的估算公式如下：

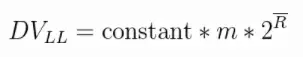
HyperLogLog与LogLog的区别在于HyperLogLog使用的是调和平均数，并非平均数。调和平均数指的是倒数的平均数（调和平均数）。调和平均数相比平均数能降低最大值对平均值的影响，这个就好比我和马爸爸两个人一起算平均工资，如果用平均值这么一下来我也是年薪数十亿，这样肯定是不合理的。

使用平均数和调和平均数计算方式如下：

调和平均数的基本计算公式如下：

3.3 HyperLogLog的实现

根据3.1和3.2大致可以知道HyperLogLog的实现原理了，它的主要精髓在于通过记录下低位连续零位的最大长度K（也就是上面我们说的kmax），来估算随机数的数量n。

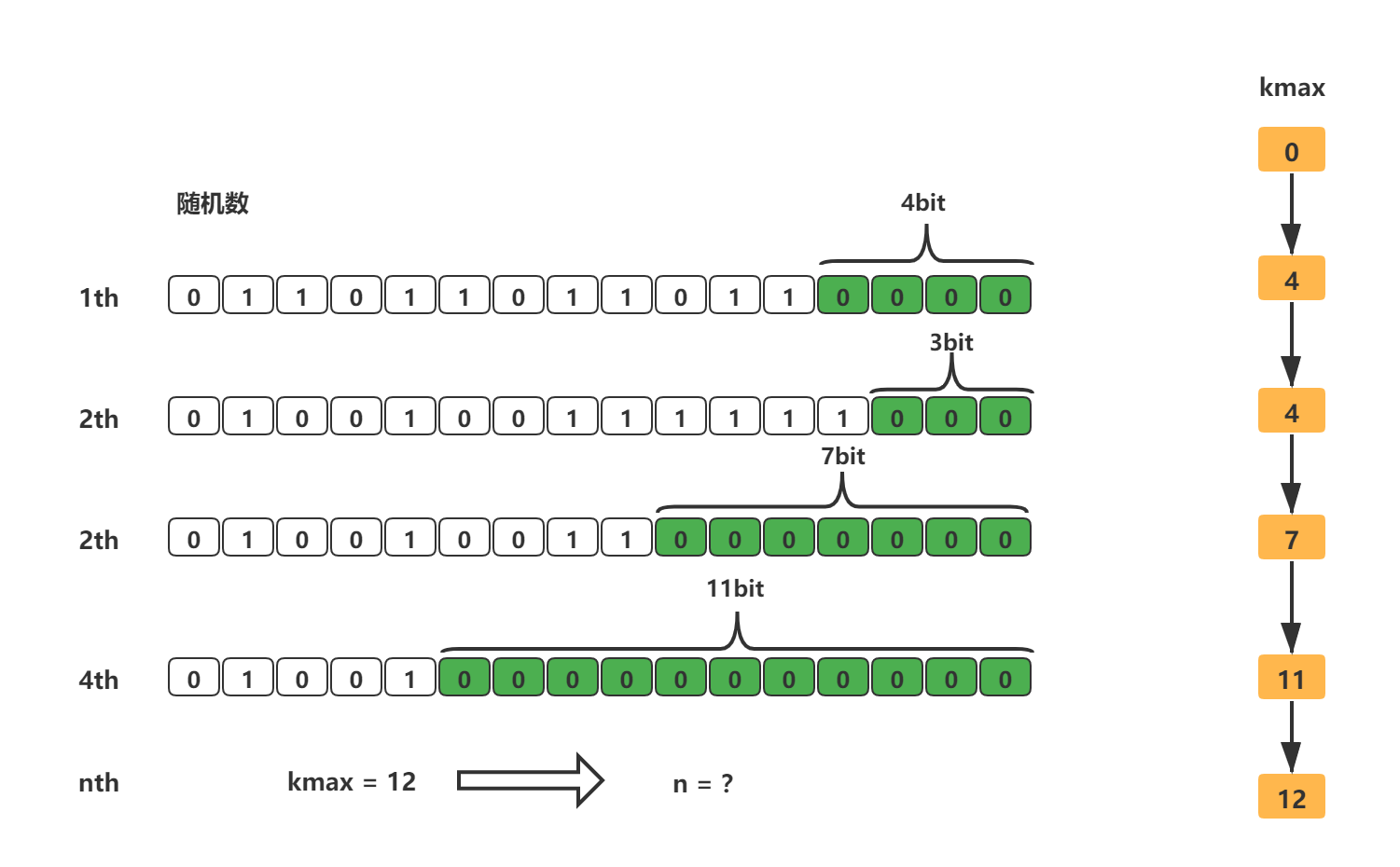
任何值在计算机中我们都可以将其转换为比特串，也就是0和1组成的bit数组，我们从这个bit串的低位开始计算，直到出现第一个1为止，这就好比上面的伯努利试验抛硬币，一直抛硬币直到出现第一个正面为止（只是这里是数字0和1，伯努利试验中使用的硬币的正与反，并没有区别）。而HyperLogLog估算的随机数的数量，比如我们统计的UV，就好比伯努利试验中试验的次数。

综上所述，HyperLogLog的实现主要分为三步：

第一步：转为比特串

通过hash函数，将输入的数据装换为比特串，比特串中的0和1可以类比为硬币的正与反，这是实现估值统计的第一步

第二步：分桶

分桶就是上面3.2估值优化中的分多轮，这样做的的好处可以使估值更加准确。在计算机中，分桶通过一个单位是bit，长度为L的大数组S，将数组S平均分为m组，m的值就是多少轮，每组所占有的比特个数是相同的，设为 P。得出如下关系：

• L = S.length
• L = m * p

• 数组S的内存 = L / 8 / 1024 (KB)

在HyperLogLog中，我们都知道它需要12KB的内存来做基数统计，原因就是HyperLogLog中m=16834，p=6，L=16834 * 6，因此内存为=16834 * 6 / 8 / 1024 = 12 (KB)，这里为何是6位来存储kmax，因为6位可以存储的最大值为64，现在计算机都是64位或32位操作系统，因此6位最节省内存，又能满足需求。

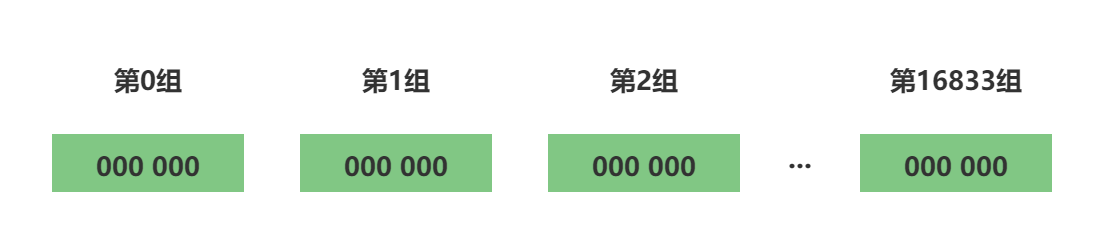
第三步：桶分配

最后就是不同的数据该如何分配桶，我们通过计算hash的方式得到比特串，只要hash函数足够好，就很难产生hash碰撞，我们假设不同的数值计算得到不同的hash值，相同的数值得到相同的hash值（这也是HyperLogLog能用来统计UV的一个关键点），此时我们需要计算值应该放到那个桶中，可以计算的方式很多，比如取值的低16位作为桶索引值，或者采用值取模的方式等等。

3.4 代码实现-BernoulliExperiment（伯努利试验）

首先来写一个3.1中伯努利试验n=2^kmax的估算值验证，这个估算值相对偏差会比较大，在试验轮次增加时估算值的偏差会有一定幅度的减小，其代码示例如下：

package com.lizba.pf;

import java.util.concurrent.ThreadLocalRandom;

/**
 * <p>
 *      伯努利试验 中基数n与kmax之间的关系  n = 2^kmax
 * </p>
 *
 * @Author: Liziba
 * @Date: 2021/8/17 23:16
 */
public class BernoulliExperimentTest {

    static class BitKeeper {

        /** 记录最大的低位0的长度 */
        private int kmax;


        public void random() {
            // 生成随机数
            long value = ThreadLocalRandom.current().nextLong(2L << 32);
            int len = this.lowZerosMaxLength(value);
            if (len > kmax) {
                kmax = len;
            }

        }

        /**
         * 计算低位0的长度
         * 这里如果不理解看下我的注释
         * value >> i 表示将value右移i,  1<= i <32 ， 低位会被移出
         * value << i 表示将value左移i,  1<= i <32 ， 低位补0
         * 看似一左一右相互抵消，但是如果value低位是0右移被移出后，左移又补回来，这样是不会变的，但是如果移除的是1，补回的是0，那么value的值就会发生改变
         * 综合上面的方法，就能比较巧妙的计算低位0的最大长度
         *
         * @param value
         * @return
         */
        private int lowZerosMaxLength(long value) {
            int i = 1;
            for (; i < 32; i++) {
                if (value >> i << i != value) {
                    break;
                }
            }
            return i - 1;
        }

    }


    static class Experiment {
        /** 测试次数n */
        private int n;
        private BitKeeper bitKeeper;

        public Experiment(int n) {
            this.n = n;
            this.bitKeeper = new BitKeeper();
        }

        public void work() {
            for(int i = 0; i < n; i++) {
                this.bitKeeper.random();
            }
        }

        /**
         * 输出每一轮测试次数n
         * 输出 logn / log2 = k 得 2^k = n，这里的k即我们估计的kmax
         * 输出 kmax，低位最大0位长度值
         */
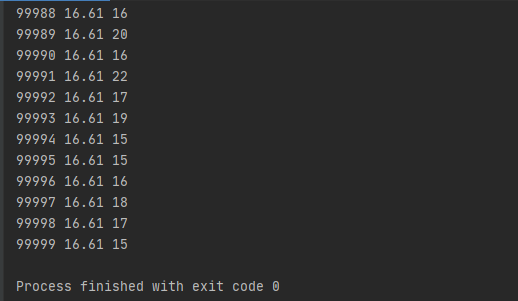
        public void debug() {
            System.out.printf("%d %.2f %d\n", this.n, Math.log(this.n) / Math.log(2), this.bitKeeper.kmax);
        }
    }

    public static void main(String[] args) {
        for (int i = 0; i < 100000; i++) {
            Experiment experiment = new Experiment(i);
            experiment.work();
            experiment.debug();
        }
    }

}

我们可以通过修改main函数中，测试的轮次，再根据输出的结果来观察，n=2^kmax这样的结果还是比较吻合的。

3.5 代码实现-HyperLogLog

接下来根据HyperLogLog中采用调和平均数+分桶的方式来做代码优化，模拟简单版本的HyperLogLog算法的实现，其代码如下：

package com.lizba.pf;

import java.util.concurrent.ThreadLocalRandom;

/**
 * <p>
 *      HyperLogLog 简单实现
 * </p>
 *
 * @Author: Liziba
 * @Date: 2021/8/18 10:40
 */
public class HyperLogLogTest {

    static class BitKeeper {

        /** 记录最大的低位0的长度 */
        private int kmax;


        /**
         * 计算低位0的长度，并且保存最大值kmax
         *
         * @param value
         */
        public void random(long value) {
            int len = this.lowZerosMaxLength(value);
            if (len > kmax) {
                kmax = len;
            }
        }

        /**
         * 计算低位0的长度
         * 这里如果不理解看下我的注释
         * value >> i 表示将value右移i,  1<= i <32 ， 低位会被移出
         * value << i 表示将value左移i,  1<= i <32 ， 低位补0
         * 看似一左一右相互抵消，但是如果value低位是0右移被移出后，左移又补回来，这样是不会变的，但是如果移除的是1，补回的是0，那么value的值就会发生改变
         * 综合上面的方法，就能比较巧妙的计算低位0的最大长度
         *
         * @param value
         * @return
         */
        private int lowZerosMaxLength(long value) {
            int i = 1;
            for (; i < 32; i++) {
                if (value >> i << i != value) {
                    break;
                }
            }
            return i - 1;
        }
    }


    static class Experiment {

        private int n;
        private int k;
        /** 分桶，默认1024，HyperLogLog中是16384个桶，并不适合我这里粗糙的算法 */
        private BitKeeper[] keepers;

        public Experiment(int n) {
            this(n, 1024);
        }

        public Experiment(int n, int k) {
            this.n = n;
            this.k = k;
            this.keepers = new BitKeeper[k];
            for (int i = 0; i < k; i++) {
                this.keepers[i] = new BitKeeper();
            }
        }

        /**
         * (int) (((m & 0xfff0000) >> 16) % keepers.length) -> 计算当前m在keepers数组中的索引下标
         * 0xfff0000 是一个二进制低16位全为0的16进制数，它的二进制数为 -> 1111111111110000000000000000
         * m & 0xfff0000 可以保理m高16位， (m & 0xfff0000) >> 16 然后右移16位，这样可以去除低16位，使用高16位代替高16位
         * ((m & 0xfff0000) >> 16) % keepers.length 最后取模keepers.length，就可以得到m在keepers数组中的索引
         */
        public void work() {
            for (int i = 0; i < this.n; i++) {
                long m = ThreadLocalRandom.current().nextLong(1L << 32);
                BitKeeper keeper = keepers[(int) (((m & 0xfff0000) >> 16) % keepers.length)];
                keeper.random(m);
            }
        }

        /**
         * 估算 ，求倒数的平均数，调和平均数
         *
         * @return
         */
        public double estimate() {
            double sumBitsInverse = 0.0;
            // 求调和平均数
            for (BitKeeper keeper : keepers) {
                sumBitsInverse += 1.0 / (float) keeper.kmax;
            }
            double avgBits = (float) keepers.length / sumBitsInverse;
            return Math.pow(2, avgBits) * this.k;
        }

    }

    /**
     * 测试
     *
     * @param args
     */
    public static void main(String[] args) {
        for (int i = 100000; i < 1000000; i+=100000) {
            Experiment experiment = new Experiment(i);
            experiment.work();
            double estimate = experiment.estimate();
            // i 测试数据
            // estimate 估算数据
            // Math.abs(estimate - i) / i 偏差百分比
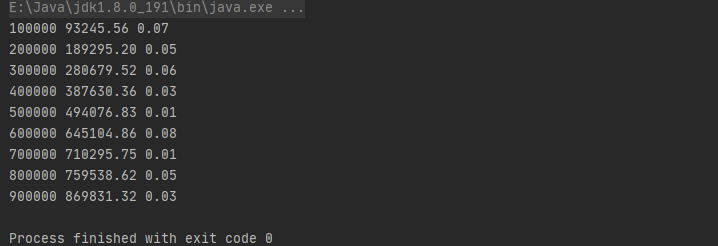
            System.out.printf("%d %.2f %.2f\n", i, estimate, Math.abs(estimate - i) / i);
        }
    }

}

测试结果如下，误差基本控制在0.08以下，还是很高的误差，所以说算法很粗糙

三、Geospatial

1、简介

Geospatial是Redis在3.2版本以后增加的地理位置GEO模块，这个模块可以用来实现微信附近的人，在线点餐“附近的餐馆”等位置功能。

2、命令

2.1 GEOADD

命令简介：

将给定的空间元素（维度、经度、名字）添加到指定的键里面，数据以有序集合的形式被存放在键中。GEOADD接收的参数必须先输入经度，然后输入维度。

GEOADD经纬度的输入范围如下（对两极不支持）：

1. 有效经度介于-180°~180°之间
2. 有效维度介于-85.05112878°至85.05112878°之间

当用户尝试输入一个超出范围的经度或者纬度时， GEOADD 命令将返回一个错误。

代码示例：

可以依次添加单个，也可以同时添加多个地理位置的元素。

127.0.0.1:6379> geoadd city 116.405289 39.904987 beijing
(integer) 1
127.0.0.1:6379> geoadd city 117.190186 39.125595 tianjin
(integer) 1
127.0.0.1:6379> geoadd city 121.472641 31.231707 shanghai
(integer) 1
127.0.0.1:6379> geoadd city 112.982277 28.19409 changsha 113.28064 23.125177 guangzhou
(integer) 2

错误示例：

127.0.0.1:6379> geoadd city 190 18 buzhidao
(error) ERR invalid longitude,latitude pair 190.000000,18.000000

2.2 GEOPOS

命令简介：

根据键（key）获取给定位置元素的位置（经度和纬度），GEOPOS 可以接收一个member，也可以接收多个member，如果member不存在则返回nil

代码示例：

127.0.0.1:6379> geopos beijing
(empty array)
127.0.0.1:6379> geopos city beijing
1) 1) "116.40528827905654907"
   2) "39.90498588819134085"
127.0.0.1:6379> geopos city tianjin shanghai
1) 1) "117.19018846750259399"
   2) "39.12559461779084558"
2) 1) "121.47264093160629272"
   2) "31.23170744181923197"
127.0.0.1:6379> geopos city xiaoriben
1) (nil)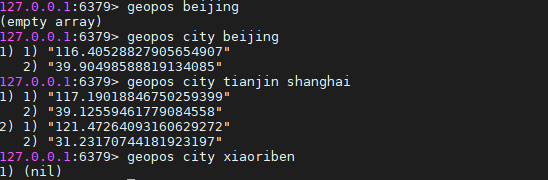

2.3 GEODIST 

命令简介：

返回两个给定位置之间的距离，以双精度浮点数的形式被返回。如果给定的位置其中一个不存在（两个都不存在也是一样，下面有示例），将会返回空值（nil）。

unit单位描述：

• m -> 米
• km -> 千米

• mi -> 英里
• ft -> 英尺

默认单位：

如果用户未给定指定单位unit，则默认为米（m）

误差范围：

GEODIST 计算的算法会将地球考虑为一个完全球体，在极限情况下，存在最大0.5%的误差

代码示例：

127.0.0.1:6379> geodist city beijing shanghai m
"1067597.0432"
127.0.0.1:6379> geodist city beijing shanghai km
"1067.5970"
127.0.0.1:6379> geodist city beijing xiaoriben
(nil)
127.0.0.1:6379> geodist city meiguoguizi xiaoriben
(nil)

2.4 GEORADIUS

命令简介：

以给定的经纬度为中心， 返回键包含的位置元素当中， 与中心的距离不超过给定最大距离的所有位置元素。

m|km|ft|mi选项：

• m -> 米
• km -> 千米

• mi -> 英里
• ft -> 英尺

[WITHCOORD] [WITHDIST] [WITHHASH]选项：

• [WITHCOORD]：将位置元素的经度和纬度也一并返回。
• [WITHDIST] ：在返回位置元素的同时， 将位置元素与中心之间的距离也一并返回。 距离的单位和用户给定的范围单位保持一致。

• [WITHHASH]： 以 52 位有符号整数的形式， 返回位置元素经过原始 geohash 编码的有序集合分值。 这个选项主要用于底层应用或者调试， 实际中的作用并不大。

[ASC|DESC] 选项：

• ASC：根据给定的中心位置，从近到远返回位置元素
• DESC：根据给定的中心位置，从远到近返回位置元素

[COUNT count] 参数：

GEORADIUS 默认会返回符合条件的全部位置元素。但是用户可以通过[COUNT count] 参数去指定获取前N个匹配元素。这个参数可以减少需要返回的元素数量，一定程度上可以减少带宽压力。

返回值：

GEORADIUS 的返回值是一个数组，但是数组的内容会根据是否存在上述参数而改变

• 未给定任何WITH参数，则返回普通线性列表
• 给定[WITHCOORD] [WITHDIST] [WITHHASH]等参数后返回一个二层嵌套数组

具体返回值请查看后续示例，建议还是自己多搞几次就清楚了

代码示例：

未给定任何WITH参数

127.0.0.1:6379> georadius city 116.405289 39.904987 1000 km
1) "tianjin"
2) "beijing"

给定[WITHCOORD] [WITHDIST] [WITHHASH]等参数，返回的时二层嵌套数组

127.0.0.1:6379> georadius city 116.405289 39.904987 1000 km withcoord
1) 1) "tianjin"
   2) 1) "117.19018846750259399"
      2) "39.12559461779084558"
2) 1) "beijing"
   2) 1) "116.40528827905654907"
      2) "39.90498588819134085"

127.0.0.1:6379> georadius city 116.405289 39.904987 1000 km withdist
1) 1) "tianjin"
   2) "109.7754"
2) 1) "beijing"
   2) "0.0001"

2.5 GEORADIUSBYMEMBER

命令简介：

GEORADIUSBYMEMBER与GEORADIUS的区别在于，GEORADIUSBYMEMBER无需给定经纬度，只需要给定成员的key就行，具体使用与GEORADIUS一致

代码示例：

127.0.0.1:6379> georadiusbymember city beijing 1000 km
1) "tianjin"
2) "beijing"

127.0.0.1:6379> georadiusbymember city beijing 1000 km withcoord
1) 1) "tianjin"
   2) 1) "117.19018846750259399"
      2) "39.12559461779084558"
2) 1) "beijing"
   2) 1) "116.40528827905654907"
      2) "39.90498588819134085"

2.6 GEOHASH

命令名称：

返回一个或多个位置元素的GeoHash表示，可以给顶多个key中的member，因此返回的是一个数组。

代码示例：

127.0.0.1:6379> geohash city beijing shanghai changsha
1) "wx4g0b7xru0"
2) "wtw3sjt9vs0"
3) "wt026ux4mz0"

3、中国省会城市的经纬度

为了便于各位大佬们学习Geospatial的学习，我整理了全国省会城市的经纬度在这，有需要的可以自取。

名称	经度	维度
北京市	116.405289	39.904987
天津市	117.190186	39.125595
呼和浩特市	111.751990	40.841490
银川市	106.232480	38.486440
石家庄市	114.502464	38.045475
济南市	117.000923	36.675808
郑州市	113.665413	34.757977
西安市	108.948021	34.263161
武汉市	114.298569	30.584354
南京市	118.76741	32.041546
合肥市	117.283043	31.861191
上海市	121.472641	31.231707
长沙市	112.982277	28.19409
南昌市	115.892151	28.676493
杭州市	120.15358	30.287458
福州市	119.306236	26.075302
广州市	113.28064	23.125177
台北市	121.5200760	25.0307240
海口市	110.199890	20.044220
南宁市	108.320007	22.82402
重庆市	106.504959	29.533155
昆明市	102.71225	25.040609
贵阳市	106.713478	26.578342
成都市	104.065735	30.659462
兰州市	103.834170	36.061380
西宁市	101.777820	36.617290
拉萨市	91.11450	29.644150
乌鲁木齐市	87.616880	43.826630
沈阳市	123.429092	41.796768
长春市	125.324501	43.886841
哈尔滨市	126.642464	45.756966
香港	114.165460	22.275340
澳门	113.549130	22.198750