Python求解江苏小升初数学题与图像阴影绘制

举报
小小明-代码实体 发表于 2021/10/11 22:31:12 2021/10/11
【摘要】 大家好，我是小小明。 前面我已经用Python求积分解决了一道小学数学题，详见：Python神器可以拯救小学数学题不会做 结果今天又碰到一道更难的，题目如下： 今天我们将尝试尽量多的通过Pyth...

大家好，我是小小明。

前面我已经用Python求积分解决了一道小学数学题，详见：Python神器可以拯救小学数学题不会做

结果今天又碰到一道更难的，题目如下：

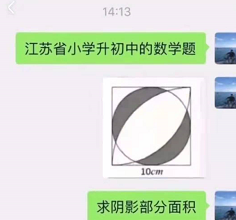
image-20210701130056863

今天我们将尝试尽量多的通过Python来解题。

首先我们以左下角为原点建立直角坐标系，很快能够知道圆的方程为 ( x − 5 ) 2 + ( y − 5 ) 2 = 5 2 (x-5)^2+(y-5)^2=5^2 (x−5)2+(y−5)2=52

两个扇形的方程分别为 ( x − 10 ) 2 + y 2 = 1 0 2 (x-10)^2+y^2=10^2 (x−10)2+y2=102和 x 2 + ( y − 10 ) 2 = 1 0 2 x^2+(y-10)^2=10^2 x2+(y−10)2=102的一部分。

上面的方程很容易得到，但要计算出方程表达式还需费一番功夫，所以下面我们打算也让Python来计算。

在解题前，我们会先用Python绘制出如下图像：

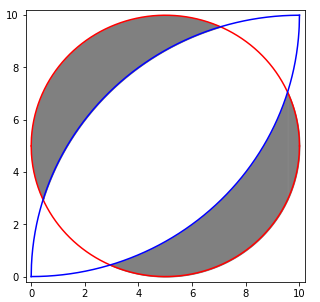
image-20210701152530497

绘图步骤

画圆

首先计算出上半圆和下半的表达式分别为：

from sympy.abc import x, y
import sympy

c1, c2 = sympy.solve((x-5)**2+(y-5)**2 - 5**2, y)
display(c1)
display(c2)

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    •

结果：

5 − − x ( x − 10 ) \displaystyle 5 - \sqrt{- x \left(x - 10\right)} 5−−x(x−10) ​

x ( 10 − x ) + 5 \displaystyle \sqrt{x \left(10 - x\right)} + 5 x(10−x) ​+5

如果想要展开表达式可以进行如下操作：

display(sympy.expand(c1))
display(sympy.expand(c2))

  
 
    
  
  • 1
    • 
  
  • 2
    •

结果：

5 − − x 2 + 10 x \displaystyle 5 - \sqrt{- x^{2} + 10 x} 5−−x2+10x ​

− x 2 + 10 x + 5 \displaystyle \sqrt{- x^{2} + 10 x} + 5 −x2+10x ​+5

直接打印可以看到在Python的表达式：

print(str(c1))
print(str(c2))

  
 
    
  
  • 1
    • 
  
  • 2
    • 
 
5 - sqrt(-x*(x - 10))
sqrt(x*(10 - x)) + 5

  
 
    
  
  • 1
    • 
  
  • 2
    •

因此利用上述文本，我们可以直接进行numpy的函数求值，下面尝试画个圆试一下：

import numpy as np
from numpy import sqrt
import matplotlib.pyplot as plt

%matplotlib inline

plt.figure(figsize=(5, 5))
x = np.linspace(0, 10, 1024)

plt.plot(x, eval(str(c1)), color="r")
plt.plot(x, eval(str(c2)), color="r")

plt.xlim(-0.2, 10.2)
plt.ylim(-0.2, 10.2)

plt.show()

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    •

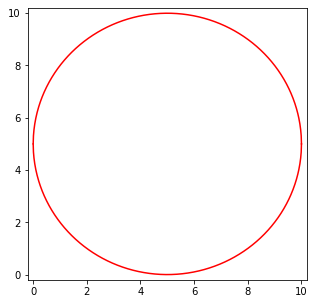
image-20210701132530107

可以看到我们求解的两个表达式可以画出圆形。

下面我们继续来画扇形：

画扇形

两个扇形的方程分别为 ( x − 10 ) 2 + y 2 = 1 0 2 (x-10)^2+y^2=10^2 (x−10)2+y2=102和 x 2 + ( y − 10 ) 2 = 1 0 2 x^2+(y-10)^2=10^2 x2+(y−10)2=102的一部分。

首先我们计算上面的扇形的函数公式：

sympy.solve((x-10)**2+y**2 - 10**2, y)

  
 
    
  
  • 1
    •

结果：

[sqrt(x*(20 - x)), -sqrt(-x*(x - 20))]

  
 
    
  
  • 1
    •

显然上面的扇形的函数公式是正数，可以直接取角标为0的函数公式：

s1, _ = sympy.solve((x-10)**2+y**2 - 10**2, y)
s1

  
 
    
  
  • 1
    • 
  
  • 2
    •

结果：

x ( 20 − x ) \displaystyle \sqrt{x \left(20 - x\right)} x(20−x) ​

用同样的方法我们再求出下面的扇形：

s2, _ = sympy.solve(x**2+(y-10)**2 - 10**2, y)
s2

  
 
    
  
  • 1
    • 
  
  • 2
    •

结果：

10 − 100 − x 2 \displaystyle 10 - \sqrt{100 - x^{2}} 10−100−x2 ​

然后我们绘制函数图形验证一下：

import numpy as np
from numpy import sqrt
import matplotlib.pyplot as plt
from sympy.abc import x, y
import sympy

%matplotlib inline

c1, c2 = sympy.solve((x-5)**2+(y-5)**2 - 5**2, y)
s1, _ = sympy.solve((x-10)**2+y**2 - 10**2, y)
s2, _ = sympy.solve(x**2+(y-10)**2 - 10**2, y)

x = np.linspace(0, 10, 1024)

plt.figure(figsize=(5, 5))
plt.plot(x, eval(str(c1)), color="r")
plt.plot(x, eval(str(c2)), color="r")

plt.plot(x, eval(str(s1)), color="b")
plt.plot(x, eval(str(s2)), color="b")

plt.xlim(-0.2, 10.2)
plt.ylim(-0.2, 10.2)

plt.show()

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    •

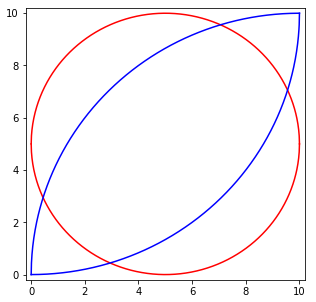
image-20210701140018826

绘制阴影

首先我们需要求出四个交点。

先分清几个线各是哪条：

import numpy as np
from numpy import sqrt
import matplotlib.pyplot as plt
from sympy.abc import x, y
import sympy

%matplotlib inline

c1, c2 = sympy.solve((x-5)**2+(y-5)**2 - 5**2, y)
s1, _ = sympy.solve((x-10)**2+y**2 - 10**2, y)
s2, _ = sympy.solve(x**2+(y-10)**2 - 10**2, y)

x = np.linspace(0, 10, 1024)

plt.figure(figsize=(5, 5))
plt.plot(x, eval(str(c1)), label="c1")
plt.plot(x, eval(str(c2)), label="c2")

plt.plot(x, eval(str(s1)), label="s1")
plt.plot(x, eval(str(s2)), label="s2")

plt.xlim(-0.2, 10.2)
plt.ylim(-0.2, 10.2)
plt.legend()

plt.show()

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    •

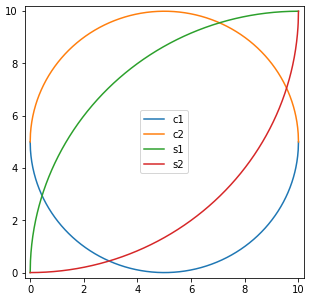
image-20210701141021791

下面分别交出交点：

from sympy.abc import x, y

x1, = sympy.solve(c1-s1, x)
x2, = sympy.solve(c1-s2, x)
x3, = sympy.solve(c2-s1, x)
x4, = sympy.solve(c2-s2, x)
x1, x2, x3, x4

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
 
(15/4 - 5*sqrt(7)/4,
 25/4 - 5*sqrt(7)/4,
 5*sqrt(7)/4 + 15/4,
 5*sqrt(7)/4 + 25/4)

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    •

根据对称性，我们可以知道四个交点的坐标分别为(x1,x2), (x2,x1), (x3,x4),(x4,x3)

同样可以画图验证一下：

import numpy as np
from numpy import sqrt
import matplotlib.pyplot as plt
from sympy.abc import x, y
import sympy

%matplotlib inline

c1, c2 = sympy.solve((x-5)**2+(y-5)**2 - 5**2, y)
s1, _ = sympy.solve((x-10)**2+y**2 - 10**2, y)
s2, _ = sympy.solve(x**2+(y-10)**2 - 10**2, y)
x1, = sympy.solve(c1-s1, x)
x2, = sympy.solve(c1-s2, x)
x3, = sympy.solve(c2-s1, x)
x4, = sympy.solve(c2-s2, x)

x = np.linspace(0, 10, 1024)

plt.figure(figsize=(5, 5))
plt.plot(x, eval(str(c1)), label="c1")
plt.plot(x, eval(str(c2)), label="c2")

plt.plot(x, eval(str(s1)), label="s1")
plt.plot(x, eval(str(s2)), label="s2")

plt.plot([x1, x2, x3, x4], [x2, x1, x4, x3], 'rx')
plt.text(x1, x2+0.1, "p1", ha="center", va="bottom")
plt.text(x2, x1+0.1, "p2", ha="center", va="bottom")
plt.text(x3, x4+0.1, "p3", ha="center", va="bottom")
plt.text(x4, x3+0.1, "p4", ha="center", va="bottom")

plt.xlim(-0.2, 10.2)
plt.ylim(-0.2, 10.2)
plt.legend()
plt.show()

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    • 
  
  • 34
    • 
  
  • 35
    •

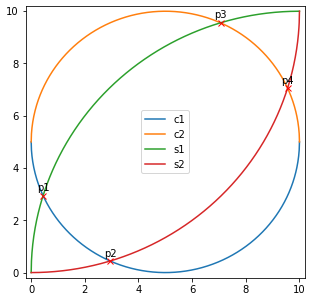
image-20210701145551263

下面开始绘制阴影：

import numpy as np
from numpy import sqrt
import matplotlib.pyplot as plt
from sympy.abc import x, y
import sympy

%matplotlib inline

c1, c2 = sympy.solve((x-5)**2+(y-5)**2 - 5**2, y)
s1, _ = sympy.solve((x-10)**2+y**2 - 10**2, y)
s2, _ = sympy.solve(x**2+(y-10)**2 - 10**2, y)
x1 = sympy.solve(c1-s1, x)[0].evalf()
x2 = sympy.solve(c1-s2, x)[0].evalf()
x3 = sympy.solve(c2-s1, x)[0].evalf()
x4 = sympy.solve(c2-s2, x)[0].evalf()


x = np.linspace(0, 10, 1024)
c1, c2, s1, s2 = map(lambda s: eval(str(s)), (c1, c2, s1, s2))

plt.figure(figsize=(5, 5))
plt.plot(x, c1, label="c1")
plt.plot(x, c2, label="c2")
plt.plot(x, s1, label="s1")
plt.plot(x, s2, label="s2")

plt.fill_between(x[x <= x1], c1[x <= x1], c2[x <= x1], color="grey")
plt.fill_between(x[(x1 < x) & (x <= x3)], s1[(x1 < x) &
                 (x <= x3)], c2[(x1 < x) & (x <= x3)], color="grey")
plt.fill_between(x[(x2 <= x) & (x <= x4)], c1[(x2 <= x) & (
    x <= x4)], s2[(x2 <= x) & (x <= x4)], color="grey")
plt.fill_between(x[x > x4], c1[x > x4], c2[x > x4], color="grey")

plt.plot([x1, x2, x3, x4], [x2, x1, x4, x3], 'rx')

plt.xlim(-0.2, 10.2)
plt.ylim(-0.2, 10.2)
plt.legend()
plt.show()

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    • 
  
  • 34
    • 
  
  • 35
    • 
  
  • 36
    • 
  
  • 37
    • 
  
  • 38
    • 
  
  • 39
    •

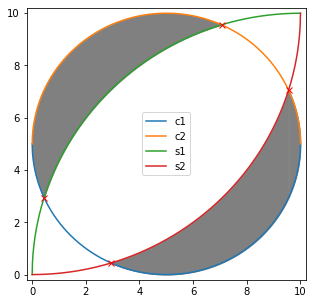
image-20210701152317342

然后再稍微调整一下颜色即可得到文章开头的图像：

绘图完整代码

import numpy as np
from numpy import sqrt
import matplotlib.pyplot as plt
from sympy.abc import x, y
import sympy

%matplotlib inline

c1, c2 = sympy.solve((x-5)**2+(y-5)**2 - 5**2, y)
s1, _ = sympy.solve((x-10)**2+y**2 - 10**2, y)
s2, _ = sympy.solve(x**2+(y-10)**2 - 10**2, y)
x1 = sympy.solve(c1-s1, x)[0].evalf()
x2 = sympy.solve(c1-s2, x)[0].evalf()
x3 = sympy.solve(c2-s1, x)[0].evalf()
x4 = sympy.solve(c2-s2, x)[0].evalf()


x = np.linspace(0, 10, 1024)
c1, c2, s1, s2 = map(lambda s: eval(str(s)), (c1, c2, s1, s2))

plt.figure(figsize=(5, 5))
plt.plot(x, c1, label="c1", color="r")
plt.plot(x, c2, label="c2", color="r")
plt.plot(x, s1, label="s1", color="b")
plt.plot(x, s2, label="s2", color="b")

plt.fill_between(x[x <= x1], c1[x <= x1], c2[x <= x1], color="grey")
plt.fill_between(x[(x1 < x) & (x <= x3)], s1[(x1 < x) &
                 (x <= x3)], c2[(x1 < x) & (x <= x3)], color="grey")
plt.fill_between(x[(x2 <= x) & (x <= x4)], c1[(x2 <= x) & (
    x <= x4)], s2[(x2 <= x) & (x <= x4)], color="grey")
plt.fill_between(x[x > x4], c1[x > x4], c2[x > x4], color="grey")

plt.xlim(-0.2, 10.2)
plt.ylim(-0.2, 10.2)
plt.show()

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    • 
  
  • 34
    • 
  
  • 35
    • 
  
  • 36
    •

在完成图像绘制后，我们就可以通过相同的思路求积分得到面积了：

积分求解面积

最终结果完整求解代码：

from sympy.abc import x, y
from sympy import integrate
import sympy

c1, c2 = sympy.solve((x-5)**2+(y-5)**2 - 5**2, y)
s1, _ = sympy.solve((x-10)**2+y**2 - 10**2, y)
s2, _ = sympy.solve(x**2+(y-10)**2 - 10**2, y)
x1 = sympy.solve(c1-s1, x)[0].evalf()
x2 = sympy.solve(c1-s2, x)[0].evalf()
x3 = sympy.solve(c2-s1, x)[0].evalf()
x4 = sympy.solve(c2-s2, x)[0].evalf()

r = integrate(c2-c1, (x, 0, x1))+integrate(c2-s1, (x, x1, x3)) + \
    integrate(s2-c1, (x, x2, x4))+integrate(c2-c1, (x, x4, 10))
r.round(8)

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    •

结果：29.27625191

如果希望得到更加精确的的结果，可以最后再调用evalf方法：

from sympy.abc import x, y
from sympy import integrate
import sympy

c1, c2 = sympy.solve((x-5)**2+(y-5)**2 - 5**2, y)
s1, _ = sympy.solve((x-10)**2+y**2 - 10**2, y)
s2, _ = sympy.solve(x**2+(y-10)**2 - 10**2, y)
x1, = sympy.solve(c1-s1, x)
x2, = sympy.solve(c1-s2, x)
x3, = sympy.solve(c2-s1, x)
x4, = sympy.solve(c2-s2, x)

r = integrate(c2-c1, (x, 0, x1))+integrate(c2-s1, (x, x1, x3)) + \
    integrate(s2-c1, (x, x2, x4))+integrate(c2-c1, (x, x4, 10))
r.evalf()

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    •

结果：29.2762519060696

文章来源: xxmdmst.blog.csdn.net，作者：小小明-代码实体，版权归原作者所有，如需转载，请联系作者。

原文链接：xxmdmst.blog.csdn.net/article/details/118388505

【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱： cloudbbs@huaweicloud.com
Python
  • 点赞
  • 收藏
  • 关注作者

评论（0）

0/1000
抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认 取消

加入云驻计划，成为创作者

  • 华为云周边好礼
  • 免费体验产品
  • 特殊身份标识
  • 线下官方门票
  • 内部专家零距离
  • 与10000+优质创作者共同成长
立即加入