pygraphviz的安装与红黑树可视化
【摘要】
大家好，我是小小明，今天我将带大家安装pygraphviz，并通过它对红黑树这种数据结构进行可视化。
pygraphviz的安装与红黑树的可视化
安装graphviz
下载地址：http://www...
大家好，我是小小明，今天我将带大家安装pygraphviz，并通过它对红黑树这种数据结构进行可视化。
pygraphviz的安装与红黑树的可视化
安装graphviz
下载地址：http://www.graphviz.org/download/
windows平台下可以选择：
安装完成后将bin目录添加到环境变量中。
验证安装：
C:\Users\Administrator>dot -version
dot - graphviz version 2.38.0 (20140413.2041)
libdir = "D:\Program Files (x86)\Graphviz2.38\bin"
Activated plugin library: gvplugin_dot_layout.dll
Using layout: dot:dot_layout
Activated plugin library: gvplugin_core.dll
Using render: dot:core
Using device: dot:dot:core
The plugin configuration file:
D:\Program Files (x86)\Graphviz2.38\bin\config6
was successfully loaded.
render : cairo dot fig gd gdiplus map pic pov ps svg tk vml vrml xdot
layout : circo dot fdp neato nop nop1 nop2 osage patchwork sfdp twopi
textlayout : textlayout
device : bmp canon cmap cmapx cmapx_np dot emf emfplus eps fig gd gd2 gif gv ima
p imap_np ismap jpe jpeg jpg metafile pdf pic plain plain-ext png pov ps ps2 svg svgz tif
tiff tk vml vmlz vrml wbmp xdot xdot1.2 xdot1.4
loadimage : (lib) bmp eps gd gd2 gif jpe jpeg jpg png ps svg
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
出现类似上面的版本信息，表示安装成功。
安装pygraphviz
下载地址：https://github.com/CristiFati/Prebuilt-Binaries/tree/master/PyGraphviz
从上面地址下载指定python版本的pygraphviz，我下载的是64位系统python3.7版本：
然后在下载目录中运行以下命令即可安装成功：
pip install pygraphviz-1.5-cp37-cp37m-win_amd64.whl
- 1
红黑树的概念
平衡二叉查找树中“平衡”的意思，其实就是让整棵树左右看起来比较“对称”、比较“平衡”，不要出现左子树很高、右子树很矮的情况。这样就能让整棵树的高度相对来说低一些，相应的插入、删除、查找等操作的效率高一些。
平衡二叉查找树的初衷，是为了解决二叉查找树因为动态更新导致的性能退化问题。
红黑树（Red-Black Tree，简称 R-B Tree）是最常用的平衡二叉查找树，除此之外平衡二叉查找树还有Splay Tree（伸展树）、Treap（树堆）等。它是一种不严格的平衡二叉查找树，
红黑树中的节点，一类被标记为黑色，一类被标记为红色。
红黑树满足：
- 根节点是黑色的；
- 每个叶子节点都是黑色的空节点（NIL），叶子节点不存储数据；
- 任何相邻的节点都不能同时为红色，红色节点是被黑色节点隔开的；
- 每个节点，从该节点到达其可达叶子节点的所有路径都包含相同数目的黑色节点；
如何比较轻松学会红黑树：
第一点，把红黑树的平衡调整的过程比作魔方复原，不要过于深究这个算法的正确性。只需要明白，只要按照固定的操作步骤，保持插入、删除的过程，不破坏平衡树的定义就行了。
第二点，找准关注节点，不要搞丢、搞错关注节点。因为每种操作规则，都是基于关注节点来做的，只有弄对了关注节点，才能对应到正确的操作规则中。在迭代的调整过程中，关注节点在不停地改变，所以，这个过程一定要注意，不要弄丢了关注节点。
第三点，插入操作的平衡调整比较简单，但是删除操作就比较复杂。针对删除操作，我们有两次调整，第一次是针对要删除的节点做初步调整，让调整后的红黑树继续满足第四条定义，“每个节点到可达叶子节点的路径都包含相同个数的黑色节点”。但是这个时候，第三条定义就不满足了，有可能会存在两个红色节点相邻的情况。第二次调整就是解决这个问题，让红黑树不存在相邻的红色节点。
红黑树的实现代码（含可视化）
# -*- coding: UTF-8 -*-
from collections import deque
from typing import Optional
import pygraphviz as pgv
class TreeNode:
def __init__(self, data=None, color=None):
self.data = data
assert color in ['r', 'b']
self.color = 'red' if color == 'r' else 'black'
self.left = None
self.right = None
self.parent = None
def is_black(self) -> bool:
return self.color == 'black'
def is_red(self) -> bool:
return self.color == 'red'
def set_black(self):
self.color = 'black'
def set_red(self):
self.color = 'red'
class RedBlackTree:
def __init__(self, val_list=None):
self.tree: Optional[TreeNode] = None
self.black_leaf = TreeNode(color='b') # 共用的黑色叶子节点
if val_list is None:
val_list = []
for n in val_list:
self.insert(n)
def find(self, data) -> Optional[TreeNode]:
if self.tree is None:
return None
p = self.tree
while p != self.black_leaf:
if data < p.data:
p = p.left
elif data > p.data:
p = p.right
else:
return p
return None
def insert(self, data):
new_node = TreeNode(data, 'r') # 新插入的节点为红色
# 根节点
if self.tree is None:
self.tree = new_node
else:
p = self.tree # 根节点
while p != self.black_leaf: # 黑色叶子节点
pp = p # pp表示插入点的父节点
if data < p.data:
p = p.left
elif data > p.data:
p = p.right
else:
# raise KeyError('val:{} already exists' % data) # 该值已存在，插入失败
return
if data < pp.data:
pp.left = new_node
else:
pp.right = new_node
new_node.parent = pp
new_node.left = new_node.right = self.black_leaf
# 插入后调整
self._insert_fixup(new_node)
def _insert_fixup(self, node):
n: TreeNode = node # 关注节点
while n != self.tree and n.parent.is_red():
# 父p 叔u 祖父g
p = self.parent(n)
u = self.bro(p)
g = self.parent(p)
if u.is_red(): # case 1 叔叔节点是红色
p.set_black() # 父节点设置成黑色
u.set_black() # 叔叔节点设置成黑色
g.set_red() # 祖父节点设置成红色
n = g # 关注节点变成祖父节点
continue
# 往下走，说明叔叔节点是黑色
if p == g.left: # 父节点为祖父节点的左子结点
if n == p.right: # case 2 关注节点是其父节点的右子节点
self.rotate_l(p) # 围绕关注节点的父节点左旋
n, p = p, n # 左旋后指针交换，关注节点设置为关注节点的父节点
# case 3 关注节点是其父节点的左子节点
p.set_black() # 关注节点的父节点设置为黑色
g.set_red() # 关注节点的祖父节点设置为红色
self.rotate_r(g) # 围绕关注节点的祖父节点右旋
else: # 父节点为祖父节点的右子结点
if n == p.left: # case 2 关注节点是其父节点的左子节点
self.rotate_r(p) # 围绕关注节点的父节点右旋
n, p = p, n # 右旋后指针交换，关注节点设置为关注节点的父节点
# case 3 关注节点是其父节点的右子节点
p.set_black() # 关注节点的父节点设置为黑色
g.set_red() # 关注节点的祖父节点设置为红色
self.rotate_l(g) # 围绕关注节点的祖父节点左旋
# 根节点强制置黑，有两种情况根节点是红色：
# 1. 新插入时是红色
# 2. 经过case 1调整过后变红色
self.tree.color = 'black'
def delete(self, data):
n: TreeNode = self.find(data)
if n is None:
return
# n的子节点个数等于2
if self.children_count(n) == 2:
# 寻找n的后继s
s = n.right
while s.left != self.black_leaf:
s = s.left
n.data = s.data
# 将删除n转化为删除s
n = s
# n的子节点个数小于2
if n.left == self.black_leaf:
c = n.right
else:
c = n.left
self._transplant(n, c)
# 删除的节点是黑色，需要调整
if n.is_black():
self._delete_fixup(c)
return
def _delete_fixup(self, node):
n = node
while n != self.tree and n.is_black():
p = self.parent(n)
b = self.bro(n)
# 左右节点对称
if p.left == n:
if not b.is_black():
b.set_black() # case 1
p.set_red() # case 1
self.rotate_l(p) # case 1
# new bro after rotate
b = self.bro(n) # case 1
if b.left.is_black() and b.right.is_black():
b.set_red() # case 2
n = p # case 2
else:
if b.right.is_black():
b.left.set_black() # case 3
b.set_red() # case 3
self.rotate_r(b) # case 3
# new bro after rotate
b = self.bro(n) # case 3
# 注意，因为p可能是红或黑，所以不能直接赋值颜色，只能copy
b.color = p.color # case 4
p.set_black() # case 4
b.right.set_black() # case 4
self.rotate_l(p) # case 4
# trick, 调整结束跳出while
n = self.tree # case 4
else:
if not b.is_black():
b.set_black() # case 1
p.set_red() # case 1
self.rotate_r(p) # case 1
# new bro after rotate
b = self.bro(n) # case 1
if b.left.is_black() and b.right.is_black():
b.set_red() # case 2
n = p # case 2
else:
if b.left.is_black():
b.right.set_black() # case 3
b.set_red() # case 3
self.rotate_l(b) # case 3
# new bro after rotate
b = self.bro(n) # case 3
# 注意，因为p可能是红或黑，所以不能直接赋值颜色，只能copy
b.color = p.color # case 4
p.set_black() # case 4
b.left.set_black() # case 4
self.rotate_r(p) # case 4
# trick, 调整结束跳出while
n = self.tree # case 4
# 将n设为黑色，从上面while循环跳出，情况有两种
# 1. n是根节点，直接无视附加的黑色
# 2. n是红色的节点，则染黑
n.set_black()
def _transplant(self, n1, n2):
"""
节点移植， n2 -> n1
:param n1: 原节点
:param n2: 移植节点
:return:
"""
if n1 == self.tree:
if n2 != self.black_leaf:
self.tree = n2
n2.parent = None
else:
self.tree = None # 只有删除根节点时会进来
else:
p = self.parent(n1)
if p.left == n1:
p.left = n2
else:
p.right = n2
n2.parent = p
def rotate_l(self, node):
if node is None:
return
if node.right is self.black_leaf:
return
p = self.parent(node)
x = node
y = node.right
# node为根节点时，p为None，旋转后要更新根节点指向
if p is not None:
if x == p.left:
p.left = y
else:
p.right = y
else:
self.tree = y
x.parent, y.parent = y, p
if y.left != self.black_leaf:
y.left.parent = x
x.right, y.left = y.left, x
def rotate_r(self, node):
if node is None:
return
if node.left is self.black_leaf:
return
p = self.parent(node)
x = node
y = node.left
# 同左旋
if p is not None:
if x == p.left:
p.left = y
else:
p.right = y
else:
self.tree = y
x.parent, y.parent = y, p
if y.right is not None:
y.right.parent = x
x.left, y.right = y.right, x
@staticmethod
def bro(node):
"""
获取兄弟节点
"""
if node is None or node.parent is None:
return None
else:
p = node.parent
if node == p.left:
return p.right
else:
return p.left
@staticmethod
def parent(node):
"""
获取父节点
"""
if node is None:
return None
else:
return node.parent
def children_count(self, node):
"""
获取子节点个数
"""
return 2 - [node.left, node.right].count(self.black_leaf)
def draw_img(self, img_name='Red_Black_Tree.png'):
"""用pygraphviz画红黑树"""
if self.tree is None:
return
tree = pgv.AGraph(directed=True, strict=True)
queue = deque([self.tree])
num = 0
while queue:
e = queue.popleft()
if e != self.black_leaf: # 黑色叶子的连线由各个节点自己画
tree.add_node(e.data, color=e.color, fontcolor="white", style="filled",
fontname="Microsoft YaHei", shape="circle", margin=0)
for c in [e.left, e.right]:
queue.append(c)
if c != self.black_leaf:
tree.add_edge(e.data, c.data, color="blue")
else:
num += 1
tree.add_node("nil%s" % num, label="Nil", color="black", fontcolor="white", style="filled",
fontname="Microsoft YaHei", shape="circle", margin=0)
tree.add_edge(e.data, "nil%s" % num, color="blue")
tree.graph_attr['epsilon'] = '0.01'
tree.layout('dot')
tree.draw(img_name)
if __name__ == '__main__':
rbt = RedBlackTree()
nums = list(range(1, 20))
for num in nums:
rbt.insert(num)
search_num = 7
n = rbt.find(search_num)
if n:
print(n.data)
else:
print('node {} not found'.format(search_num))
rbt.delete(4)
rbt.draw_img()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- 251
- 252
- 253
- 254
- 255
- 256
- 257
- 258
- 259
- 260
- 261
- 262
- 263
- 264
- 265
- 266
- 267
- 268
- 269
- 270
- 271
- 272
- 273
- 274
- 275
- 276
- 277
- 278
- 279
- 280
- 281
- 282
- 283
- 284
- 285
- 286
- 287
- 288
- 289
- 290
- 291
- 292
- 293
- 294
- 295
- 296
- 297
- 298
- 299
- 300
- 301
- 302
- 303
- 304
- 305
- 306
- 307
- 308
- 309
- 310
- 311
- 312
- 313
- 314
- 315
- 316
- 317
- 318
- 319
- 320
- 321
- 322
- 323
- 324
- 325
- 326
- 327
- 328
- 329
- 330
- 331
- 332
- 333
- 334
- 335
- 336
- 337
- 338
- 339
- 340
- 341
- 342
- 343
- 344
- 345
- 346
- 347
- 348
- 349
- 350
- 351
- 352
- 353
红黑树可视化效果
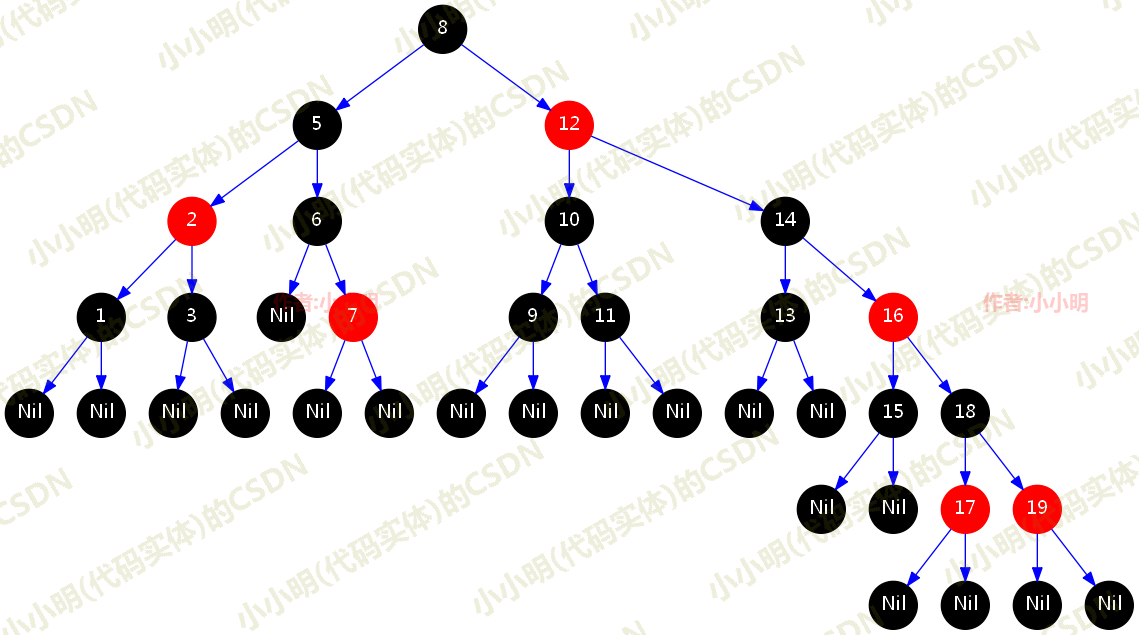
至此我们就完成了红黑树的可视化。
文章来源: xxmdmst.blog.csdn.net，作者：小小明-代码实体，版权归原作者所有，如需转载，请联系作者。
原文链接：xxmdmst.blog.csdn.net/article/details/118741732
【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱：
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者
评论（0）