【Code皮皮虾】字符串删除：两种思路，会一种即可应对面试手撕！来瞅瞅叭。

⭐题目

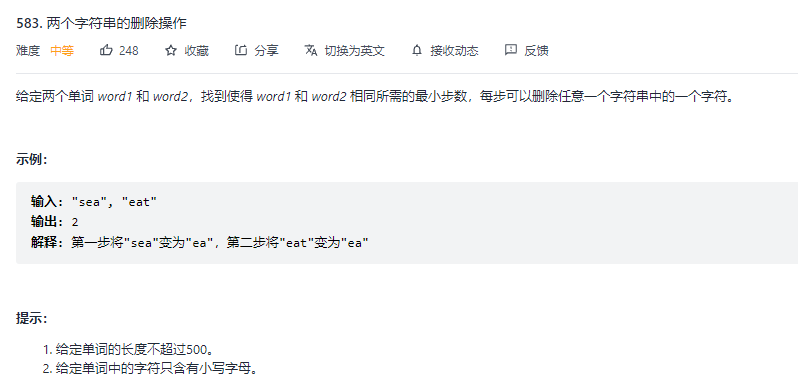
相信老司机一看就知道要用动态规划，哈哈哈，做的太多啦😂

第一个思路：最长公共子序列

题目说：找到使得 word1 和 word2 相同所需的最小步数，那我们找word1和word2的最长公共子序列，得到它的长度，再分别用word1和word2的长度减去最长公共子序列，就得到最少步数。

代码实现

class Solution {
    public int minDistance(String word1, String word2) {
        int m = word1.length(), n = word2.length();

        int[][] dp = new int[m + 1][n + 1];

        char tmp1 = ' ', tmp2 = ' ';

        for (int i = 1; i <= m; i++) {
            tmp1 = word1.charAt(i - 1);
            for (int j = 1; j <= n; j++) {
                tmp2 = word2.charAt(j - 1);
                if (tmp1 == tmp2) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        int max = dp[m][n];
        return m - max + n - max;
    }
}

第二种：正经点DP

定义dp[i][j] 为 word1前i个字符，word2前j个字符所需的最小步数

1. 当word1.charAt(i - 1) == word2.charAt(j - 1)，那么不用删除，则dp[i][j] = dp[i - 1][j - 1];
2. 当word1.charAt(i - 1) != word2.charAt(j - 1)，那么要删除一个，当然要选择最优的删，则dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + 1;

代码实现

class Solution {
    public int minDistance(String word1, String word2) {
        int m = word1.length(), n = word2.length();
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            dp[i][0] = i;
        }
        for (int j = 1; j <= n; j++) {
            dp[0][j] = j;
        }

        char tmp1 = ' ',tmp2 = ' ';

        for (int i = 1; i <= m; i++) {
            tmp1 = word1.charAt(i - 1);
            for (int j = 1; j <= n; j++) {
                tmp2 = word2.charAt(j - 1);
                
                if (tmp1 == tmp2) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + 1;
                }
            }
        }
        return dp[m][n];
    }
}

💖最后

我是 Code皮皮虾，一个热爱分享知识的 皮皮虾爱好者，未来的日子里会不断更新出对大家有益的博文，期待大家的关注！！！

创作不易，如果这篇博文对各位有帮助，希望各位小伙伴可以==一键三连哦！==，感谢支持，我们下次再见~~~