🍊作者简介：秃头小苏，致力于用最通俗的语言描述问题

🍊往期回顾：基于pytorch搭建VGGNet神经网络用于花类识别    基于pytorch搭建AlexNet神经网络用于花类识别

🍊近期目标：拥有5000粉丝
🍊支持小苏：点赞👍🏼、收藏⭐、留言📩

@[toc]

凸优化理论基础1——仿射集

  最近上的数学课着实让人头大，课上听不懂，只能下课慢慢的消化知识🥗🥗🥗凸优化可以说是直接当头一棒，第一节就完全跟不上节奏，甚至于一些基本的概念都理解不了，这样雪球越滚越大，这门课就算是荒废了🍋🍋🍋

  若是你和我有一样的尴尬处境，那么这篇文章或许能帮助到你。这一节我打算从一些基础的概念讲起，只有先对这些概率了如指掌，后面才能学的自在✈✈✈现在就让我们一起来看看叭🎨🎨🎨

直线和线段

  大家先别喷⛲⛲⛲有人想，我堂堂一位受过高等教育的大学生，你竟然给我讲直线和线段，这不是侮辱还是侮辱啊😭😭😭我们之前学过的直线大多是形如y=kx+b的形式，那么这里我们定义直线的表达式如下：

  设 ${{\rm{x}}_1} \ne {x_2}$为 ${R^n}$空间中的两个点，那么具有下列形式的点

$$y = \theta {x_1} + (1 - \theta ){x_2},\theta \in R$$

会组成一条穿越 $x_1$和 $x_2$的直线。乍一看这个公式我是懵逼的，这也是直线的方程！！！？这样我们将这个式子换一种表达方式，即把括号拆开再重新组合，如下：

$$y = {x_2} + \theta ({x_1} - {x_2}),\theta \in R$$

  那么上式该怎么解释呢？ $\theta(x_1-x_2)$表示方向从 $x_2$指向 $x_1$，大小由 $\theta$控制，则y表示基点 $x_2$和方向 $x_1-x_2$乘以参数 $\theta$的和。当 $\theta=0$时，y在 $x_2$点处；当 $\theta=1$时，y在 $x_1$点处。 $\theta$取不同的值，y对应于不同的值，这样y就可以取遍 $x_1 、x_2$所在直线上的所有点，即y表示过 $x_1 、x_2$两点的直线。这里给出图示方便大家理解：

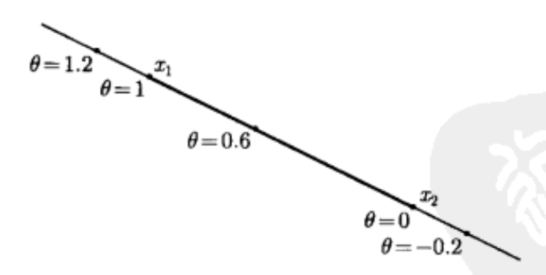
  既然我们都已经知道了直线的表达方式，那么线段就很容易了，我们只要限定 $\theta \in [0,1]$即可将y限制在 $x_1和x_2$之间，也即形成了线段，其公式如下：

$$y = \theta {x_1} + (1 - \theta ){x_2},\theta \in [0,1]$$

仿射集

• 定义

  先来给出仿射集的定义：==如果通过集合 $C\in R^n$中任意两个不同点的直线仍然在集合C中,那么称集合C是仿射的。== 由于我们前面已经给出了直线的表达式，因此这里 $C\in R^n$是仿射集可以等价为 $\Leftrightarrow$==对任意的 $x_1,x_2 \in C$ 及 $\theta \in R$ 有 $\theta {x_1} + (1 - \theta ){x_2} \in C$ 。== 换而言之,C包含了C中任意两点的系数之和为1的线性组合。

• 仿射集例子

  直线、空集、点、全空间。【个人感觉只要直线会有一点研究价值，按照定义来说空集和点是仿射集我觉得是有点牵强的🌸🌸🌸】

仿射组合

  上文谈到仿射集的概率，这是针对两个点的，其实这个概念可以推广到多个点上。即如果 $\theta_1 + \cdots +\theta_k=1$，我们即称 $\theta_1x_1 + \cdots +\theta_kx_k$形式的点为 $x_1 , \cdots ,x_k$的仿射组合。

​  我们通过仿射集的定义可以得出结论：==一个仿射集包含任意点的仿射组合，即若C是一个仿射集合， $x_1 , \cdots ,x_k \in C$，且 $\theta_1 + \cdots +\theta_k=1$，则 $\theta_1x_1 + \cdots +\theta_kx_k$仍然在C中。==

  这里我们做一个简要的证明，证明含3个点的仿射组合仍然在C中，证明如下：

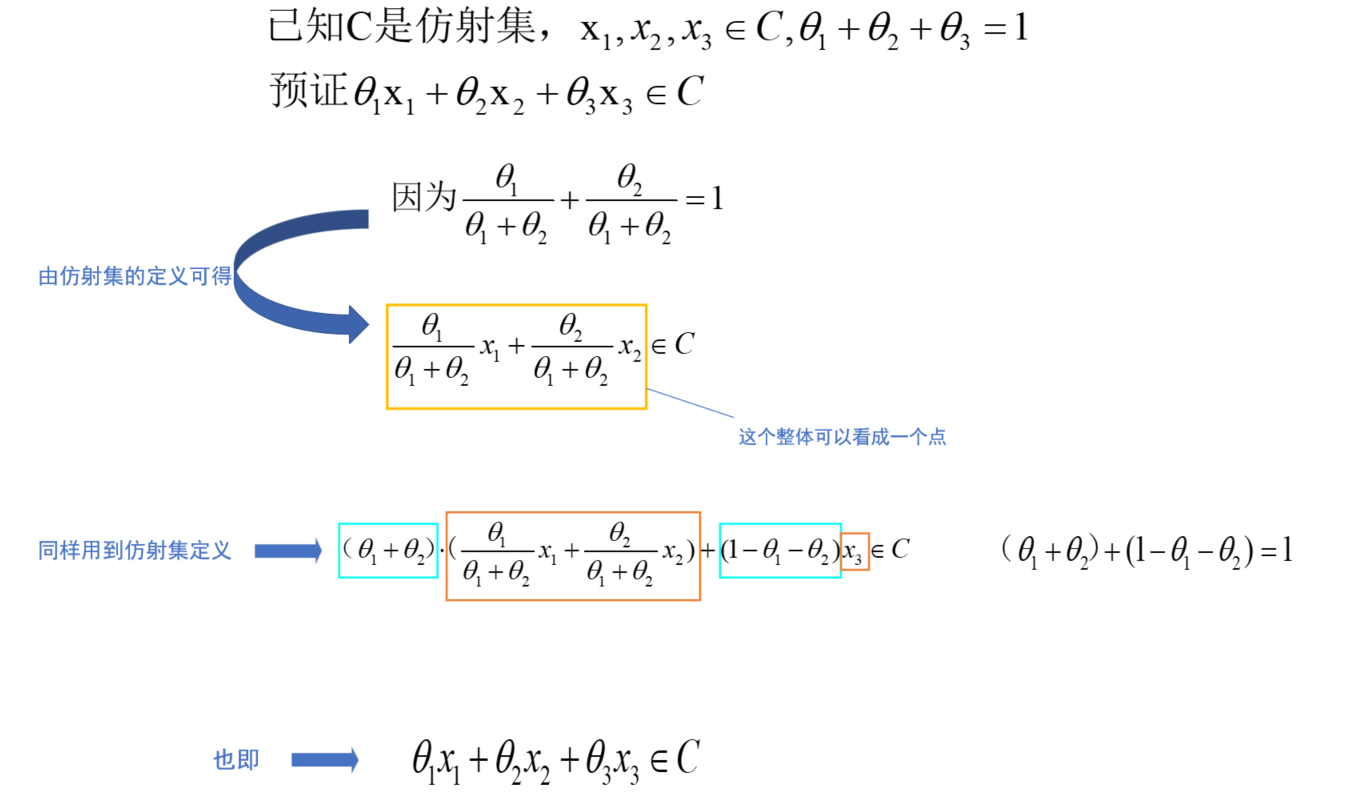
​  证明了仿射集C中的三个点的仿射组合仍然在C中，那么就可进一步证明仿射集中包含任意点的仿射组合仍在仿射集中。🍅🍅🍅

仿射集的子空间

  定义：若C是仿射集并且 $x_0 \in C$，则集合

$$V=C-x_0=\{x-x_0|x \in C \}$$

定义为仿射集C的一个子空间。

​  这里还给出一个结论，==即仿射集C的子空间V也是仿射的==，证明如下：

​  此外，仿射集的子空间关于加法和数乘是封闭的，即指子空间V中的点经过加法和数乘运算后仍然属于子空间V，证明如下：

​

子空间相当于是基 $x_0$ 做了一个平移，使之必过原点，子空间是仿射集。具体可参考视频：https://www.bilibili.com/video/BV1Xi4y1b7eF/?spm_id_from=333.788.recommend_more_video.-1

讲了这么多，我们先来看一个例题进行巩固，如下：

仿射包

  这个我不想再给出定义了，估计大家也都看烦了，那什么是仿射包呢？其实很容易理解，==仿射包就是包含集和C的最小的仿射集。== 这里我举几个例子大家可能就明白了🍜🍜🍜

• 集合C为2点，那么仿射包就是过这两点的直线🌱
• 集合C为3点，那么仿射包就是包括这三点的全平面🌱
• 集合C为4点，那么仿射包就是包括这四点的全空间🌱
• 仿射集的仿射包是它自身🌱

 
 
如若文章对你有所帮助，那就🛴🛴🛴

咻咻咻咻~~duang~~点个赞呗