[toc]

顺序表

在程序中, 经常需要一组 ( 通常是同为某个类型的 ) 数据元素作为整体管理和使用, 需要创建这种元素组, 用变量记录它们, 传进传出函数等. 一组数据中包含的元素个数可能发生变化 ( 可以增加或删除元素 ).

对于这种需求, 最简单的解决方案便是将这样一组元素看成一个序列. 用元素在序列里的位置和顺序, 表示实际应用中的某种有意义的信息, 或者表示数据之间的某种关系.

这样一组序列元素的组织形式, 我们可以将其抽象为线性表. 一个线性表是某类元素的一个集合, 还记录着元素之间的一种顺序关系. 线性表是最基本的数据结构之一, 在实际程序中应用非常广泛, 它还经常被用丛更复杂的数据结构的实现基础.

根据线性表的实际存储方式, 分为两种实现模型:

顺序表: 将元素顺序的存放在一块连续的存储区里, 元素间的顺序关系由它们的存储顺序自然表示.

链表: 将元素存放在通过链接构造起来的一系列存储块中.

a = [1,2,3] ( 4byte * 3)

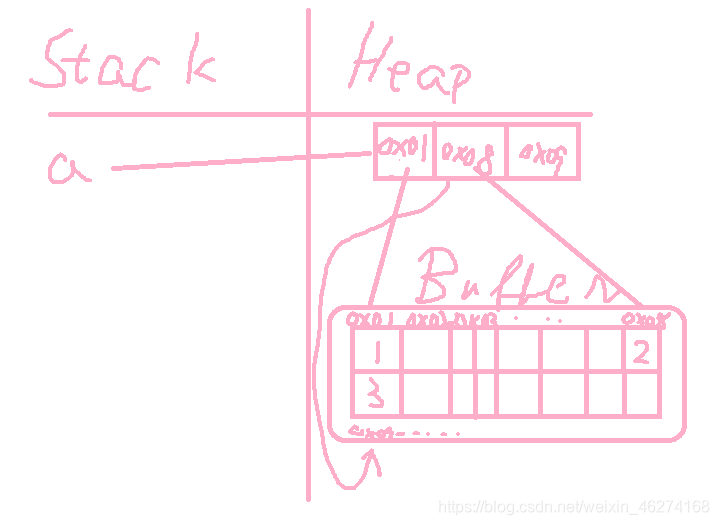
注: 听说夸我图画的好看的宝宝们都走上了人生巅峰

顺序表的基本形式

上图表示的是顺序列表的基本形式, 数据元素本身连续存储, 每个元素所占的存储单元大小固定相同, 元素的下标是其逻辑地址, 而元素存储的物理地址 ( 实际内存地址 ) 可以通过存储区的起始地址 Loc(e0) 加上逻辑地址 ( 第 i 个元素 ) 与存储单元大小 ( c ) 的乘积计算而得, 即:

Loc(ei) = Loc(e0) + c*i

故, 访问指定元素时无需从头遍历, 通过计算便可获得对应地址, 其时间复杂度为 O(1).

如果元素的大小不统一, 则必须采用图右边的元素外置形式, 将实际数据元素另行存储, 而顺序表中各单元位置保存对应元素的地址信息 ( 即链接 ). 由于每个链接所需的存储量相同, 通过上述公式, 可以计算出元素链接的存储位置, 而后顺着链接找到实际存储的数据元素. 注意, 图右边的 c 不再是数据元素的大小, 而是存储一个链接地址所需的存储量, 这个量通常很小.

右图这样的顺序表也被称为对实际数据的索引, 这是最简单的索引结构.

文章来源: iamarookie.blog.csdn.net，作者：我是小白呀，版权归原作者所有，如需转载，请联系作者。

原文链接：iamarookie.blog.csdn.net/article/details/109195179