数据结构的本质

数据结构本质其实就是数据的存储方式。

学习数据结构，选择合理数据结构存储数据，为高效利用数据提供了基础。

举个例子：

比如 1,2,3,“a”,“b”,“c” 这种数据数据，我们利用变量或者数组存储即可 。

还有一种数据，比如家族的族谱这种树形结构的数据 ，当然了 你也可以用线性表或者变量来存储，但却丢失了其中的逻辑关系，为后续使用数据带来了非常大的困难。针对此类数据，数据结构中使用树结构来存储这类数据。

再比如，导航软件大家都使用过，如果你使用线性结构来储存，那… 针对此类数据，数据结构提供了图存储结构存储这类数据。

常用数据结构

• 线性表，还可细分为顺序表、链表、栈和队列；
• 树结构，比如普通树，二叉树，线索二叉树等等
• 图存储结

线性表（一对一）

线性表结构存储的数据往往是可以依次排列的，具备这种“一对一”关系的数据就可以使用线性表来存储。 。

线性表并不是一种具体的存储结构，它包含顺序存储结构和链式存储结构，是顺序表和链表的统称。

顺序表

最常用的顺序表就是数组，比如你开辟一个 长度为5的int类型的数组，存储 1 3 5 7 9 ，在内存中的存储结构如下

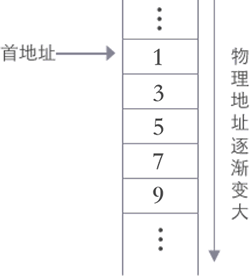
顺序表结构的底层实现借助的就是数组，去理解顺序表的话，可以把顺序等价为数组，但实则不是这样的。

链表

我们知道，顺序表（底层实现靠数组) 需要提前申请一定大小的存储空间，这块存储空间的物理地址是连续的

链表则完全不同，使用链表存储数据时，是随用随申请，因此数据的存储位置是相互分离的，即数据的存储位置是随机的。

为了给各个数据块建立“依次排列”的关系，链表给各数据块增设一个指针，每个数据块的指针都指向下一个数据块，最后一个数据块的指针指向 NUL，这样一来，看似毫无关系的数据块就建立了“依次排列”的关系，也就形成了链表。

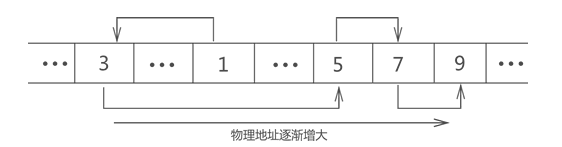
栈

栈和队列隶属于线性表，是特殊的线性表，因为它们对线性表中元素的进出做了明确的要求。

栈中的元素只能从线性表的一端进出（另一端封死），且要遵循“先入后出”的原则，即先进栈的元素后出栈。

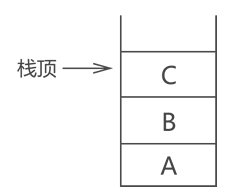
栈结构如上图所示，像一个木桶，栈中含有 3 个元素，分别是 A、B 和 C，从在栈中的状态可以看出 A 最先进的栈，然后 B 进栈，最后 C 进栈。

根据“先进后出 FILO”的原则，3 个元素出栈的顺序应该是：C 最先出栈，然后 B 出栈，最后才是 A 出栈。

队列

队列中的元素只能从线性表的一端进，从另一端出，且要遵循“先入先出 FIFO”的特点，即先进队列的元素也要先出队列

队列结构如上图所示，队列中有 3 个元素，分别是 A、B 和 C，从在队列中的状态可以看出是 A 先进队列，然后 B 进，最后 C 进。

根据“先进先出”的原则，3 个元素出队列的顺序应该是 A 最先出队列，然后 B 出，最后 C 出。

树存储结构 （一对多）

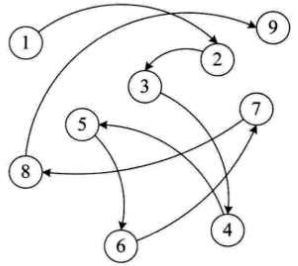
树存储结构适合存储具有“一对多”关系的数据。

可以把上面的这个图想象成一个家族族谱 ， 拿2来举例，2有一个父亲1，有2个孩子 4和5 ，这就是“一对多”的关系，满足这种关系的数据可以使用树存储结构。

图存储结构（多对多）

图存储结构适合存储具有“多对多”关系的数据。

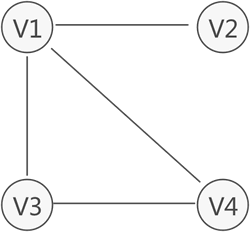
上图存储 V1、V2、V3、V4 的图结构，从图中可以清楚的看出数据之间具有的"多对多"关系。

例如，V1 与V2 V3 V2 建立着联系，V4 与 V1 和 V3 建立着联系，以此类推。满足这种关系的数据可以使用图存储结构。

逻辑结构 VS 物理存储结构

可参考： 数据结构，物理结构，存储结构，逻辑结构的区分

当一个结构，如数组、链表、树、图，在逻辑结构中只有一种定义，而在物理结构中却有两种选择，那么这个结构就属于逻辑结构； 反之，当此结构在原有基础上加上了某种限定，使得其在物理结构中只有一种定义，那么这个结构就属于物理（存储）结构；

举例1：栈属于什么结构？

—> 栈在逻辑结构中只能属于线性结构，而在物理结构中它可以使用顺序存储（数组），也可以使用链式存储（链表），所以说栈是一种逻辑结构。

算法的比较： 高斯求和为例

public class Summary {

    public static void main(String[] args) {
        int sum = 0 ,n = 100 ;      // 执行1次

        for (int i = 1; i < 101 ; i++) {   // 执行n+1次
            sum += i ;  // 执行n次
        }
        System.out.println(sum); // 执行1次

        // 时间复杂度  1 + (n+1) + n + 1 = 2n + 3 ----> 忽略常量 ----> O(n)

        // 1   +  2 +  3  + 4  +  5 + .... + 100
        // 100 +  99 + 98 + 97 +  96 + ... + 1
        //  101 + 101 + 101+ 101 +101 + ...+ 101 ---> 2 * sum
        sum = (1+ n ) * n /2 ;   // 执行1次
        System.out.println(sum);  // 执行1次

        // 时间复杂度  1 + 1 = 2 ----> 忽略常量 ----> O(1)

    }
}



  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
 

1. 第一种算法 循环N次，时间复杂度 O(n)
2. 第二种算法 相当于另一种求等差数列的算法，执行一次，时间复杂度O(1）
   高下立判 ，这就是不同的算法，不同的效率.

文章来源: artisan.blog.csdn.net，作者：小小工匠，版权归原作者所有，如需转载，请联系作者。

原文链接：artisan.blog.csdn.net/article/details/103864716