[toc]

二项分布 ( Bernouli Distribution )

设随机变量 X 服从参数为 n,p 二项分布.

设 Xi 为第 i 次试验中事件 A 发生的次数, i = 1,2,3,...,n

则: 

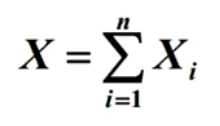
显然, Xi 相互独立均服从采纳数为 p 的 0-1 分布, 所以 

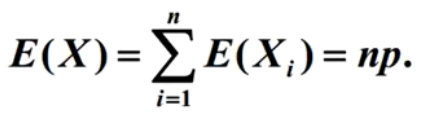
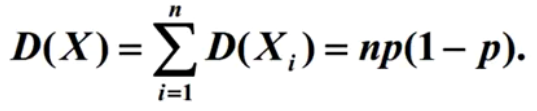
泊松分布 ( Poisson Distribution )

在实际事例中, 当一个随机事件, 以固定的平均瞬时速率 λ ( 或称密度 )随机且独立地出现时.

那么这个事件在单位时间 ( 面积或体积 ) 内出现的次数就近似地服从泊松分布 P(λ).

• 某一服务设施在一定时间内到达的人数
• 电话交换机接到呼叫的次数
• 汽车站态的候客人数
• 机器出现的故障数
• 自然灾害发生的次数
• 一块产品上的缺陷数
• 显微镜下单位分区内的细菌分布数
• 某放射物质单位时间发射出的粒子数

设 X ~ π(λ), 且分布律为

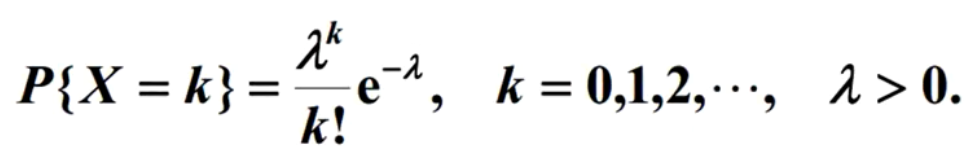
则有:

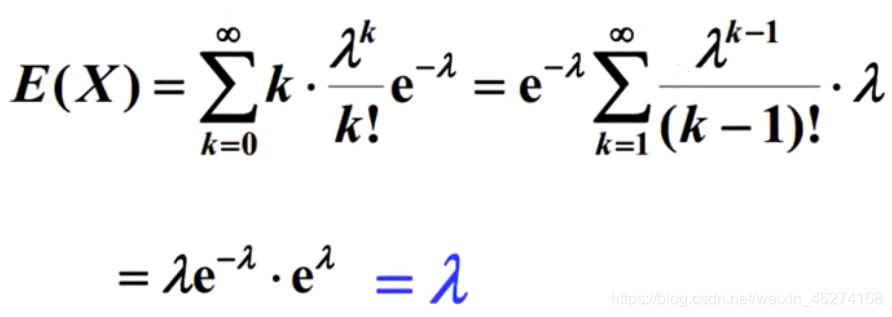
文章来源: iamarookie.blog.csdn.net，作者：我是小白呀，版权归原作者所有，如需转载，请联系作者。

原文链接：iamarookie.blog.csdn.net/article/details/109794793