概述

特征选择 (future selection): 目的是剔除不相关 (irrelevant) 或冗余 (redundant) 的特征, 从而达到减少特征个数.

特征选择就是单纯地从提取到的所有特征中选择部分特征作为训练集特征. 特征在选择在选择前和选择后可以改变值, 也不该变值. 但是选择后的特征维数肯定比选择前小, 毕竟我们只选择了其中的一部分特征.

主要方法

1. Filter (过滤式): VarianceThreshold
2. Embedd (嵌入式): 正则化, 决策树
3. Wrapper (包裹式)

VarianceThreshold 语法

VarianceThreshold(threshold = 0.0) 删除所有低方差特征

  

 

  
1
 

Variance.fit_transform(X)

• X: numpy array 格式的数据[n_samples, n_features]
• 返回值:训练集差异低于 threshold 的特征将被删除
• 默认值是保留所有非零方差特征, 即删除所有样本中具有相同值的特征

流程

1. 初始化 VarianceThreshold, 指定阈值方差
2. 调用 fit_transform

from sklearn.feature_selection import VarianceThreshold

def var():
    """
    特征选择: 删除低方差的特征
    :return: None
    """

    var = VarianceThreshold(threshold= 1.0)
    data = var.fit_transform([[0,2,0,3],[0,1,4,3],[0,1,1,3]])

    print(data)
    return None

if __name__ == "__main__":
    var()

输出结果:
[[0]
 [4]
 [1]]

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
 

噪点

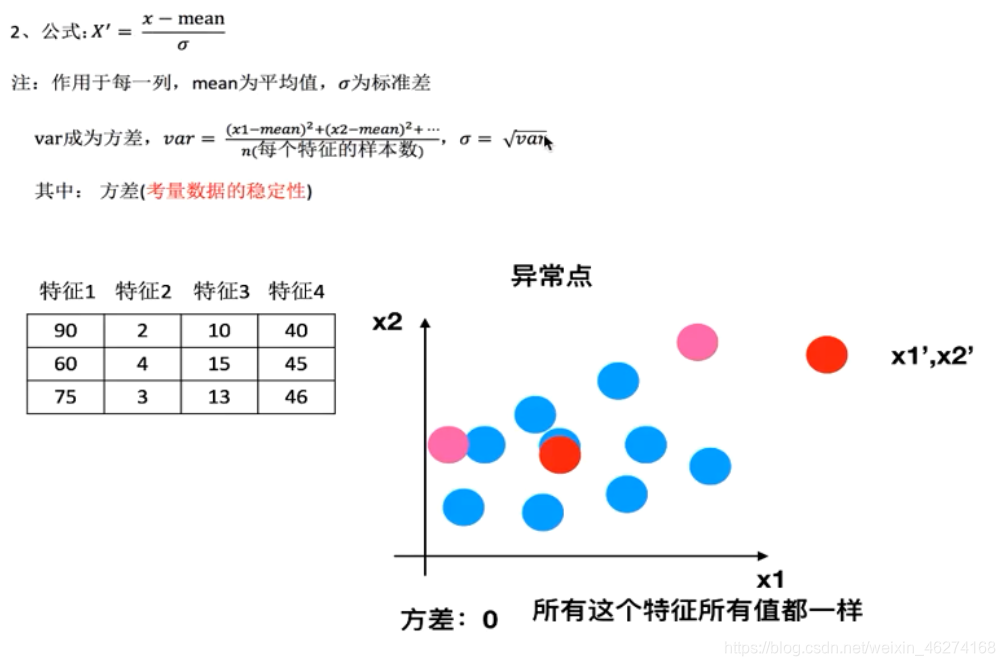
其他特征选择方法

• 神经网络

sklearn 主成分分析 API

sklearn.decomposition

PCA 是什么

本质: PCA 是一种分析, 简化数据集的技术.

目的: 是数据维数压缩, 尽可能降低原数据的维度 (复杂度), 损失少量信息.

作用: 可以削减回归分析或者聚类分析中特征的数量.

PCA 语法

PCA(n_componts=None) 将数据分解为较低维度空间

  

 

  
1
 

PCA.fit_transform(X)

• X: numpy array 格式的数据 [n_samples, n_features]
• 返回值: 转换后指定维度的 array

PCA 流程 (代码演示)

1. 初始化 PCA, 指定减少后的维度
2. 调用 fit_transform

from sklearn.decomposition import PCA

def pca():
    """
    主成分分析进行特征降维
    :return:
    """

    pca = PCA(n_components=0.9)
    data = pca.fit_transform([[2, 8, 4, 5], [6, 3, 0, 8], [5, 4, 9, 1]])

    print(data)
    return None


if __name__ == "__main__":
    pca()

输出结果:
[[ 0.          3.82970843]
 [-5.74456265 -1.91485422]
 [ 5.74456265 -1.91485422]]

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
 

文章来源: iamarookie.blog.csdn.net，作者：我是小白呀，版权归原作者所有，如需转载，请联系作者。

原文链接：iamarookie.blog.csdn.net/article/details/110790367