分布式存储

了解Redis集群原理之前我们先来梳理一下分布式存储的相关知识

拆分在算法中是一个非常重要的思想，当你的数据集巨大时，你可以按照特定的规则将大数据拆分成小数据集，降低因数据量增长过大带来的问题。

基本方案有两种：顺序分布 & 哈希分布 。 需要根据具体业务选择分片方式

数据分区虽好 ，但是有没有哪些棘手的问题要处理呢？ 当然有了，比如

• 自动负载均衡

  分布式存储系统需要自动识别负载高的节点，当某台机器的负载高时，自动将其上的部分数据迁移到其他机器。

• 一致性

  分片后数据可能分布在不同存储服务器上，无法使用数据库自带的单机事务，需通过分布式应用事务一致性模型来解决

顺序分区 Sequential partitioning

从名字上也很好理解顺序分布的含义， 就是将大表按一定顺序划分为连续的子表，然后将子表按一定策略分配到存储节点上。

举个简单的例子

优点呢？

1. 可顺序读

缺点呢？

1. 数据可能分布不均匀
2. 数据量大的时候，为了性能 ，需要使用索引来记录子表信息

哈希分区 Hash partitioning

方案总览

节点取余分区 Hashing

通过数据的某个特征计算哈希值，并将哈希值与集群中的服务器建立映射关系，从而将不同数据分布到不同服务器上。

hash(object) % N

举个例子：

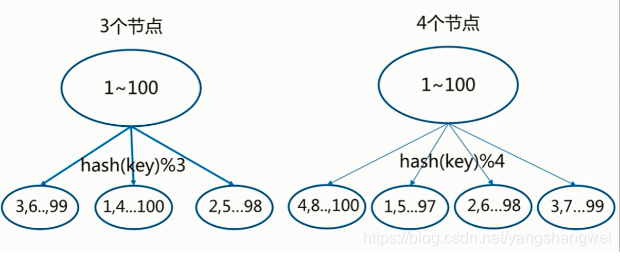
假设这个时候我要添加一个节点 ，我们拿 1-10 来说，来计算下从3个节点到4个节点的迁移率

先 1 % 3 ， 2 % 3 … 10 % 3 , 算出来 在哪个分区，如下图左侧 （0 ，1 ，2 三个分区）

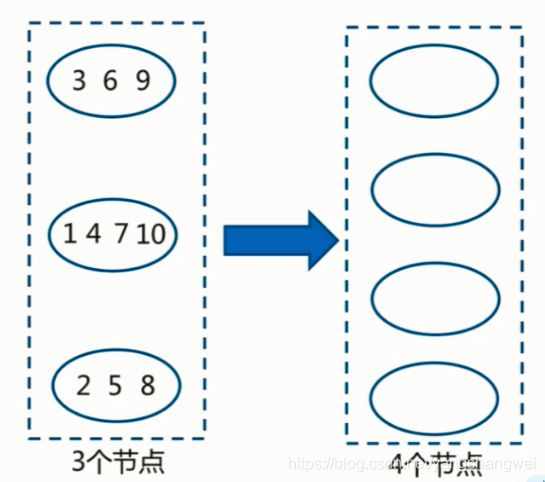
重新对4进行 1 %4 ， 2 % 4 … 10 % 4, 计算后 ，如右侧

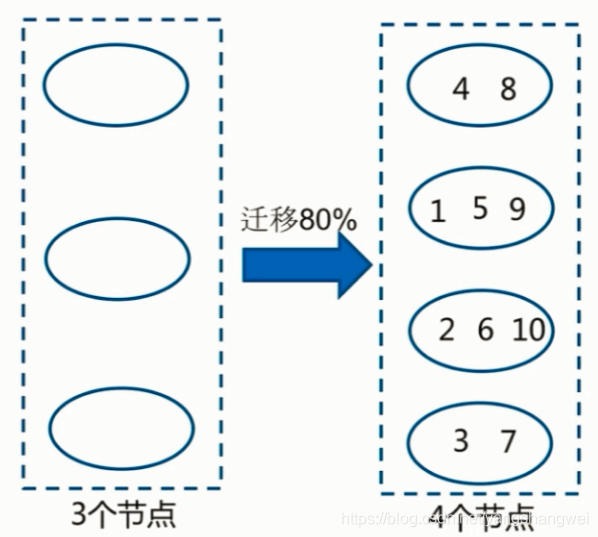
比对一下， 只有 1 (分区0) 和 2 （分区1） 这两个值 还在原来的分区里 ，其余8个数字 都迁移到了其他的分区中。

解释下迁移率 是指： 你的这个缓存区域中已经没有数据了，需要DB查询，回写到缓存，80%的数据都要这样重新构建…

咋解决呢？

稍微挫一点的方案 翻倍扩容 ，迁移率可以降低到 50%

我们还是那1-10 这10个数字，3个分区变6个分区来计算下迁移率

原来1 % 3 ， 2 % 3 … 10 % 3 , 算出来 在哪个分区
翻倍扩容 重新对6进行 1 %6 ， 2 % 6 … 10 % 6, 计算

建议： 看场景，如果你的业务对缓存依赖没这没强，查不到从DB查就是，并发也不高，也不是不可以，毕竟这个最简单。

当然了，最好不用，太古老

一致性哈希分区 Consistent hashing

刚才根据节点数量来分区的方式，缺点也看到了，迁移率太高。 刚才的翻倍扩容的方案也差强人意，有没有更好的呢？ 那就是 Consistent hashing

我们使用 哈希环来解决 slot 数发生变化时，尽量减少数据的移动。

一致性哈希算法在1997年由麻省理工学院的Karger等人在解决分布式Cache中提出的.

初始化

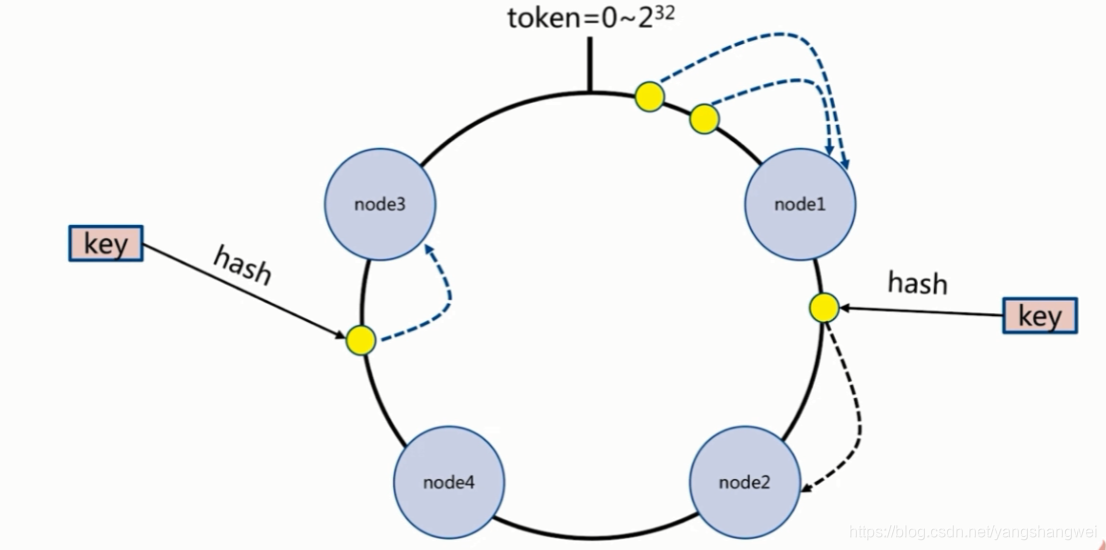
• 首先求出节点 的哈希值 （比如可以选择服务器的ip或主机名作为关键字进行哈希），并将其配置到0～2^32的环上
• 然后采用同样的方法求出存储数据的键的哈希值，并映射到相同的环上
• 紧接着从数据映射到的位置开始顺时针查找，将数据保存到找到的第一个服务器上。
• 如果超过2^32仍然找不到服务器，就会保存到第一个节点上

节点的扩容与缩容

节点取余的算法当节点动态的调整大大的影响缓存的命中率，但Consistent Hashing中，只有在环上增加服务器的地点逆时针方向的第一个节点上的键会受到影响

举个例子： 假设我们要在node1 和 node2 之间 增加一个 node5节点，看看哪些数据会受到影响？

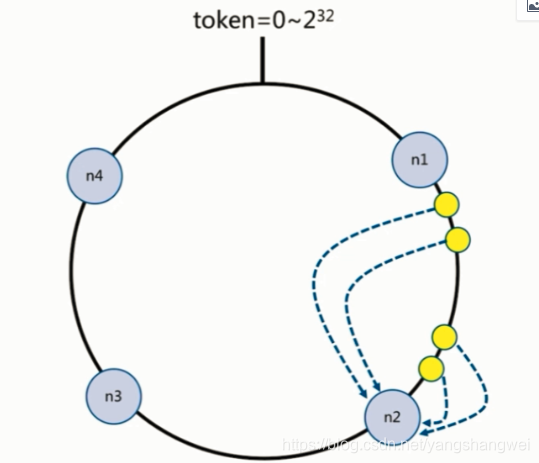
增加node5 后

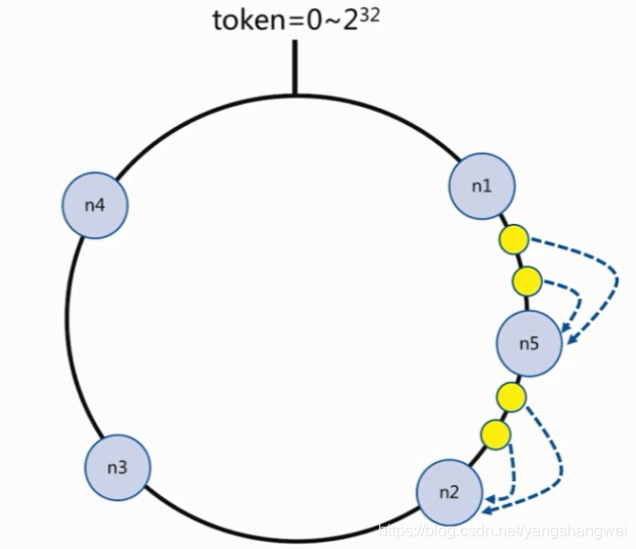
是不是 右上方的 两条数据 你下次再查找的时候 ，你会去node5找 （因为这两条数据的下一个节点是node5 ,已经不是node2了），找不到，失效了，会重新从数据源获取，重新构建。

仍然存在小规模的失效，但比第一种hash算法，如果节点很多，这种影响的数据范围降低了很多。

总结下 ：

1. 客户端分片: hash + 顺时针（优化取余）
2. 节点伸缩：只影响邻近节点，但是还有数据迁移
3. 翻倍伸缩： 保证最小迁移数据和负债均衡 ， 这个其实还是有可能数据分部不均匀，比如你4个节点，大部分的key做hash以后，有可能集中在node1 和 nod2上，node3 和 node4 只有少量的数据，所以还是建议翻倍扩容。 这个就是我们常说的： 服务节点少时数据倾斜的问题。

综上所述，一致性哈希算法对于节点的增减都只需重定位环空间中的一小部分数据，具有较好的容错性和可扩展性。

另外，一致性哈希算法在服务节点太少时，容易因为节点分部不均匀而造成数据倾斜问题

虚拟哈希分区

为了解决一致性hash在节点数量比较少的情况下出现数据倾斜问题，一致性哈希算法引入了虚拟节点机制，即对每一个服务节点计算多个哈希，每个计算结果位置都放置一个此服务节点，称为虚拟节点。

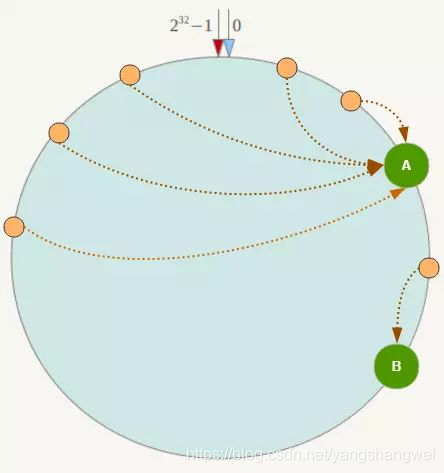
如何搞这些虚拟节点呢？ 可以在服务器ip或主机名的后面增加编号来实现。例如上面的情况，可以为每台服务器计算三个虚拟节点，于是可以分别计算 “Node A#1”、“Node A#2”、“Node A#3”、“Node B#1”、“Node B#2”、“Node B#3”的哈希值，于是形成六个虚拟节点：

同时数据定位算法不变，只是多了一步虚拟节点到实际节点的映射，例如定位到“Node A#1”、“Node A#2”、“Node A#3”三个虚拟节点的数据均定位到Node A上。

这样就解决了服务节点少时数据倾斜的问题。在实际应用中，通常将虚拟节点数设置为32甚至更大，因此即使很少的服务节点也能做到相对均匀的数据分布。

import java.util.Collection;
import java.util.HashSet;
import java.util.Iterator;
import java.util.Set;
import java.util.SortedMap;
import java.util.SortedSet;
import java.util.TreeMap;
import java.util.TreeSet;


public class ConsistentHash<T> {

    private final int numberOfReplicas;// 节点的复制因子,实际节点个数 * numberOfReplicas =
    // 虚拟节点个数
    private final SortedMap<Integer, T> circle = new TreeMap<Integer, T>();// 存储虚拟节点的hash值到真实节点的映射

    public ConsistentHash( int numberOfReplicas,
                           Collection<T> nodes) {
        this.numberOfReplicas = numberOfReplicas;
        for (T node : nodes){
            add(node);
        }
    }

    public void add(T node) {
        for (int i = 0; i < numberOfReplicas; i++){
            // 对于一个实际机器节点 node, 对应 numberOfReplicas 个虚拟节点
            /*
             * 不同的虚拟节点(i不同)有不同的hash值,但都对应同一个实际机器node
             * 虚拟node一般是均衡分布在环上的,数据存储在顺时针方向的虚拟node上
             */
            String nodestr =node.toString() + i;
            int hashcode =nodestr.hashCode();
            System.out.println("hashcode:"+hashcode);
            circle.put(hashcode, node);

        }
    }

    public void remove(T node) {
        for (int i = 0; i < numberOfReplicas; i++)
            circle.remove((node.toString() + i).hashCode());
    }

    /*
     * 获得一个最近的顺时针节点,根据给定的key 取Hash
     * 然后再取得顺时针方向上最近的一个虚拟节点对应的实际节点
     * 再从实际节点中取得 数据
     */
    public T get(Object key) {
        if (circle.isEmpty())
            return null;
        int hash = key.hashCode();// node 用String来表示,获得node在哈希环中的hashCode
        System.out.println("hashcode----->:"+hash);
        if (!circle.containsKey(hash)) {//数据映射在两台虚拟机器所在环之间,就需要按顺时针方向寻找机器
            SortedMap<Integer, T> tailMap = circle.tailMap(hash);
            hash = tailMap.isEmpty() ? circle.firstKey() : tailMap.firstKey();
        }
        return circle.get(hash);
    }

    public long getSize() {
        return circle.size();
    }

    /*
     * 查看表示整个哈希环中各个虚拟节点位置
     */
    public void testBalance(){
        Set<Integer> sets = circle.keySet();//获得TreeMap中所有的Key
        SortedSet<Integer> sortedSets= new TreeSet<Integer>(sets);//将获得的Key集合排序
        for(Integer hashCode : sortedSets){
            System.out.println(hashCode);
        }

        System.out.println("----each location 's distance are follows: ----");
        /*
         * 查看相邻两个hashCode的差值
         */
        Iterator<Integer> it = sortedSets.iterator();
        Iterator<Integer> it2 = sortedSets.iterator();
        if(it2.hasNext())
            it2.next();
        long keyPre, keyAfter;
        while(it.hasNext() && it2.hasNext()){
            keyPre = it.next();
            keyAfter = it2.next();
            System.out.println(keyAfter - keyPre);
        }
    }

    public static void main(String[] args) {
        Set<String> nodes = new HashSet<String>();
        nodes.add("A");
        nodes.add("B");
        nodes.add("C");

        ConsistentHash<String> consistentHash = new ConsistentHash<String>(2, nodes);
        consistentHash.add("D");

        System.out.println("hash circle size: " + consistentHash.getSize());
        System.out.println("location of each node are follows: ");
        consistentHash.testBalance();

        String node =consistentHash.get("apple");
        System.out.println("node----------->:"+node);
    }

}

虚拟哈希分区 (Version2)

刚才虚节点这种靠数量取胜的策略增加了存储这些虚节点信息所需要的空间。

在Redis Cluster中使用了一种比较特殊的方法来解决分布不均的问题，改进了这些数据分布的算法，将环上的空间均匀的映射到一个线性空间，这样，就保证分布的均匀性。

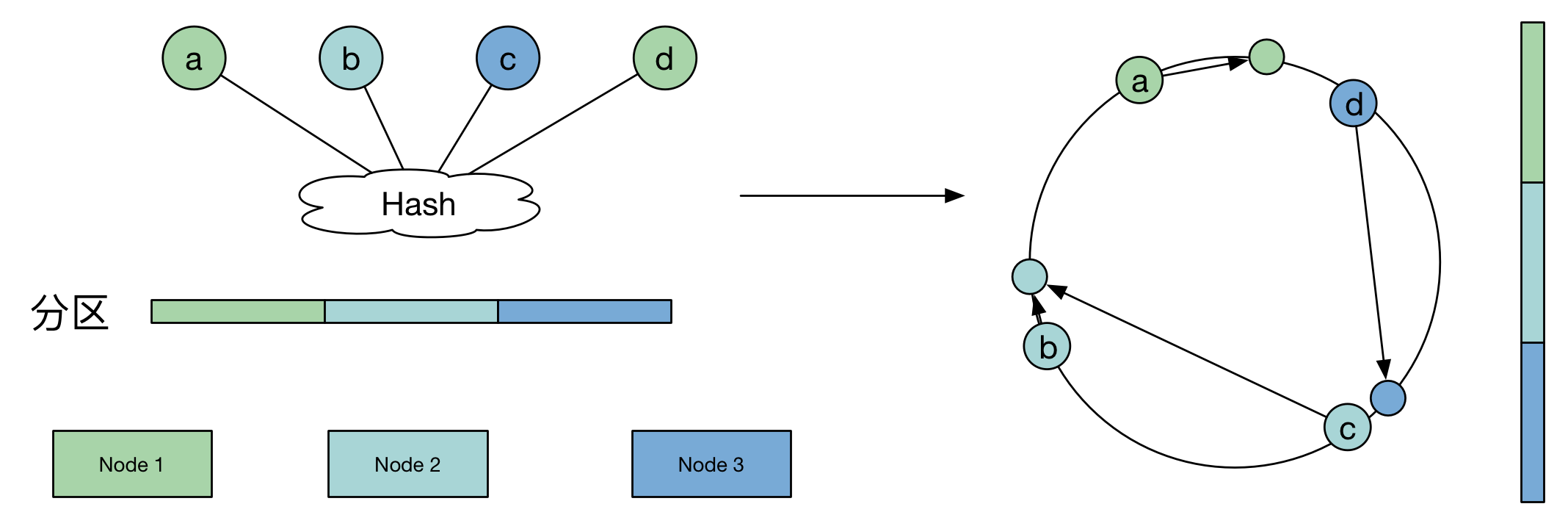
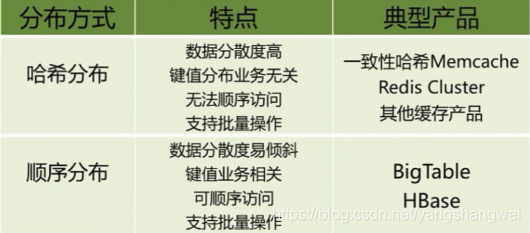
顺序分区 VS 哈希分区

文章来源: artisan.blog.csdn.net，作者：小小工匠，版权归原作者所有，如需转载，请联系作者。

原文链接：artisan.blog.csdn.net/article/details/105468108